主动式检测方法的思路是通过引入干扰打破孤岛运行下逆变器系统与负载之间的平衡，使公共节点的电压幅值或频率超出阀值范围，从而检测出孤岛。所选择的扰动必须能够使并网系统在孤岛发生时有明显的响应，可以是逆变器输出电压或电流的幅值，也可以是频率或相角，或是功率发生变化。

1.主动频率漂移法

逆变器正常并网运行时，其锁相控制功能使其输出频率保持电网频率值不变，即使在逆变器输出电流波形中添加少量频率偏移，也能在下一同步点得到修正。然而在孤岛状态下失去了电网同步基准，逆变器输出的频率将具有连续变化的趋势，频率偏移将进一步扩大，直至偏移量超出OFP/UFP保护阀值的允许。主动频率漂移法（Active Fre-quency Drift，AFD）正是利用这一原理实现孤岛检测。

引入了主动频率漂移的并网逆变器输出电流波形如图8-37中粗实线所示。其中T_g是电网电压周期，t_z是引入频率偏移产生的死区时间，t_z与电网电压周期T_g一半的比值，定义为削波系数cf（chopping fraction）：cf=2t_z/T_g。

可见，当并网逆变器控制采用这种引入频率偏移量的电流波形时，逆变器输出电流i中的基波成分i₁将始终超前于产生电流给定所用同步基准信号一个相位角：ωt_z/2。

一旦孤岛形成后，如果负载固定不变，u_P将取决于i₁。对于纯阻性负载，u_P与i₁同相位，即u_P将超前于原同步基准信号ωt_z/2相位，锁相环将调整缩短电流控制周期（即提高电流输出的频率）试图减小这个相位差，这种锁相跟踪的结果使逆变器输出频率升高，直到触发OFP/UFP保护；对于感性负载，电压本来就超前于电流，上述输出频率的升高将更快；而对于容性负载，电压滞后于电流，且容性阻抗随频率升高而降低，若这种趋势足以抵消频率上升的趋势，将可能导致AFD孤岛检测失败。

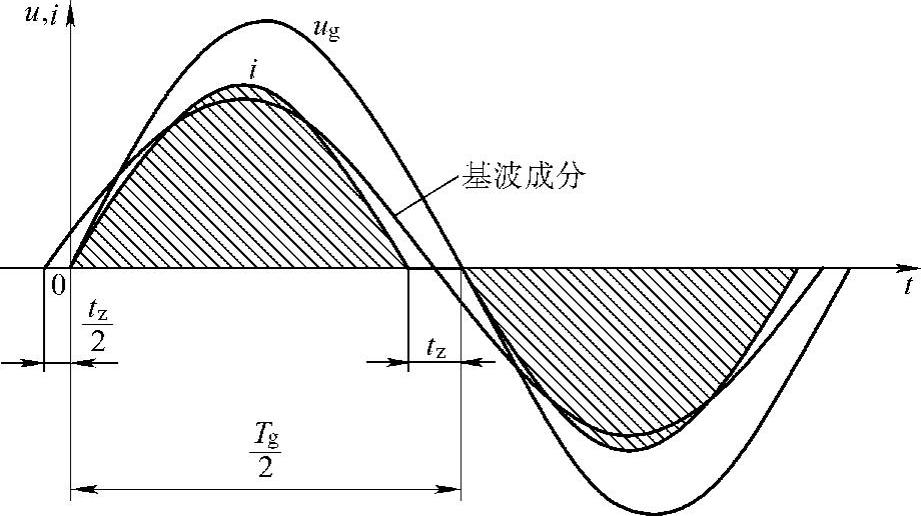
图8-37 主动频率漂移法原理

根据前述AFD检测孤岛的原理，AFD的检测盲区可用下式描述：

arctan[R（ωC-1/ωL）]≤ωt_z/2=π·cf/2（8-41）

即

根据式（8-55），确定ω阀值下选择不同的cf，即可计算绘出AFD检测盲区的边界。要注意的是，由于负载的阻抗随着频率改变而改变，绘制AFD的NDZ要同时考虑到OVP/UVP的作用。图8-38所示为1kW阻性负载（R=48.4Ω）时绘制的NDZ（相同线型包围的区域）。

可以看出，NDZ随着cf的增大而减小，当然这是以牺牲逆变器输出电流波形质量为代价的；L较大的情况下因电压响应较为平缓，电压阀值在这个范围的作用很小，主要是频率阀值起作用。

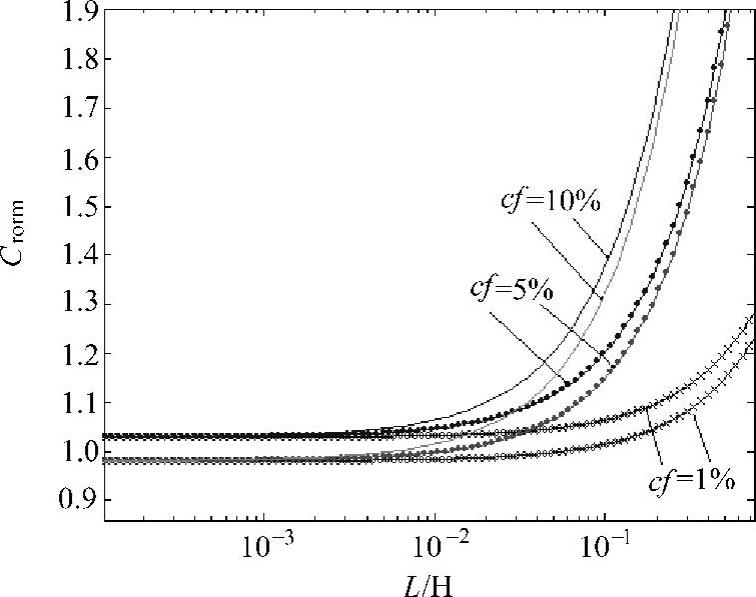
图8-38 AFD的检测盲区

2.滑模频率漂移法

滑模频率漂移法（Slide-Mode Fre_- quency Shift，SMS）检测孤岛的原理与AFD类似，两者区别主要在于：AFD通过t_z引入频率偏移，而SMS则是通过引入相角偏移θ_SMS。将逆变器电流/电压相位设计为输出电压频率的函数，在相位—频率平面上体现为一条S形相位响应曲线（见图8-39），单位功率因数并网运行时逆变器输出频率在锁相控制下稳定在S形曲线中部零相位点（图中B点）附近；而形成孤岛时，锁相环失去了电网频率基准，若频率有微小波动，S形相频特性将使相位误差继续扩大而不是减小，这种具有正反馈特性的不稳定性加剧频率变化并驱动系统趋于一个新的工作点（相频特性与负载频率特性相交点A或C）。如果这样的频率漂移范围超出OFP/UFP保护阀值的允许，那么孤岛可被检测。

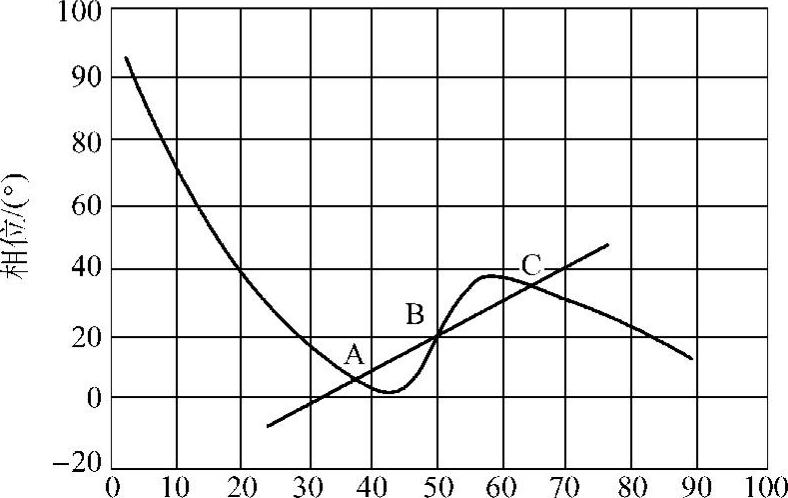
图8-39 并网逆变器输出相频特性

应用SMS进行孤岛检测时，对并网逆变器输出电流引入相位偏移θ_SMS：

式中，f为PCC节点电压的频率，f_g为电网频率，θ_m为最大相移角，f_m为对应θ_SMS=θ_m时的最大频率。

孤岛发生后，由于引入相位偏移θ_SMS，将使f增大；由式（8-44），f的增大又使θ_SMS增加。如此形成的正反馈将使f不断增加，直至超出预设的频率保护阀值。

但是SMS也存在检测盲区，对于谐振型并联RLC负载，当满足下式相位条件时，SMS失效：

其中，负载阻抗角

3.自适应频率漂移法

AFD和SMS等基于逆变器输出频率变化特性的孤岛检测方法，利用孤岛状态下逆变器输出频率失去了电网同步基准，通过逆变器内部固有的锁相控制功能驱使输出频率发生较大漂移。相对于无源检测法，频率漂移法在一定程度上减小了NDZ，添加的频率偏移量（cf或θ_SMS）越大，孤岛检测的可靠性越高，但这是以牺牲逆变器并网电流波形质量为代价的，持续添加频率扰动造成了对电网的谐波污染。

AFD和SMS在某些特殊情况下也还存在失效问题。实际上，PCC节点电压u_P在孤岛状态下不仅仅决定于逆变器输出电流，而且与负载阻抗有关，然而当采用频率漂移法时，负载阻抗随着频率的漂移变化也在发生改变，这将可能导致AFD或SMS孤岛检测失败。

逆变器正常并网状态下，锁相跟踪控制使输出电流频率跟随PCC节点电压频率（即电网频率），由于存在锁相跟踪误差，且电网频率本身也存在一定的波动误差，为防止孤岛检测误动作，应该设置一个允许频率变化的误差范围。给定一个允许公共节点电压频率变化的误差范围，当实际频率偏差在该误差范围内时，对电流频率给定添加固定偏移扰动；当实际频率偏差超出误差范围时，以正反馈方式自动增大偏移扰动量，加速公共节点电压频率的漂移并最终使之超过频率保护阀值。这种能根据频率偏差的变化自动调整频率偏移扰动量的孤岛检测方法，称之为自适应频率漂移法（Adaptive Active Frequency Drift，AAFD）。具体方法是：

（1）当PCC节点电压频率偏离电网额定频率但仍在允许误差范围内，则周期性引入一个与偏离方向相同的输出电流频率给定偏移量，也就是说这种偏移是以正反馈的形式添加的，即

式中 f_P——PCC节点电压u_P的频率；f₀——电网额定频率；

δ_f（≥0）——允许频率变化的误差量；

Δf（>δ_f）——频率偏移的大小，且（Δf+δ_f）小于OFP/UFP阀值。每隔N₁个电压周期给电流频率给定连续N₂个周期的频率偏移，而不是每个电压周期都添加，于是在大部分周期里，f=f_P，输出电流不含频率偏移带来的畸变，相对于AFD或SMS减小了对电网的谐波污染。

电网正常时，f_P必然等于电网频率且满足|f_P-f₀|≤δ_f，那么上述频率偏移仅仅是一种间隙性输出扰动而已，否则随着偏移量不断叠加，必将导致|f_P-f₀|>δ_f。

（2）当实际f_P偏离量超出δ_f时，对输出电流的频率给定添加一个与偏离方向相同的偏移量，使得

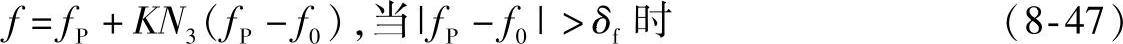
式中 K——比例系数；

N₃——控制增大频率正反馈的系数。

在同步锁相过程中，只要满足式（8-47），N₃即以自然数的整数倍逐周期递增，输出频率漂移被正反馈加速，直至频率偏移量超出OFP/UFP阀值。如果孤岛是虚假的，那么在电网同步基准作用下，f_P必然会恢复为|f_P-f₀|≤δ_f，则可将N₃复位置零，这样就可防止虚假孤岛引起误动作。

4.主动电流扰动法

对并网逆变器的输出添加周期性电流扰动，在正常并网条件下，PCC节点电压u_P受电网电压的箝位，不会受到上述扰动的影响。但当逆变器孤岛运行时，u_P=iZ，输出电流的扰动必然引起u_P的变化，只要u_P变化超出OVP/UVP保护阀值，孤岛可被检测。

理论上，主动电流扰动法不存在NDZ，即使在负载功率与逆变器输出相匹配的情况下也能实现可靠的孤岛检测，并且具有简单易行、输出谐波小等特点。但输出电流的周期性变化对逆变器自身工作影响较大，尤其对逆变器的动态性能要求较高。另外，主动电流扰动法不适用于多单元并网系统，因为当多个逆变单元同时工作时，各自产生扰动时刻不一致，对公共节点电压的影响减弱。

实际采用主动电流扰动法检测孤岛时，引入电流扰动的幅值不必要这么大，应根据OVP/UVP保护阀值选择适当的电流扰动幅值，在保证可靠前提下尽量减小扰动幅值及其对逆变器工作的影响。(www.daowen.com)

主动电流扰动法理论上不存在NDZ，也不对电网产生电流谐波污染，但要求逆变器具有较高的突变响应性能。主动电流扰动法不适用于多机并网系统，因为各逆变器产生扰动时刻不一致，单机输出电流扰动对公共节点电压的影响小，另一方面，多个电流扰动源的叠加易导致注入电网的谐波成分复杂化，影响电网质量。

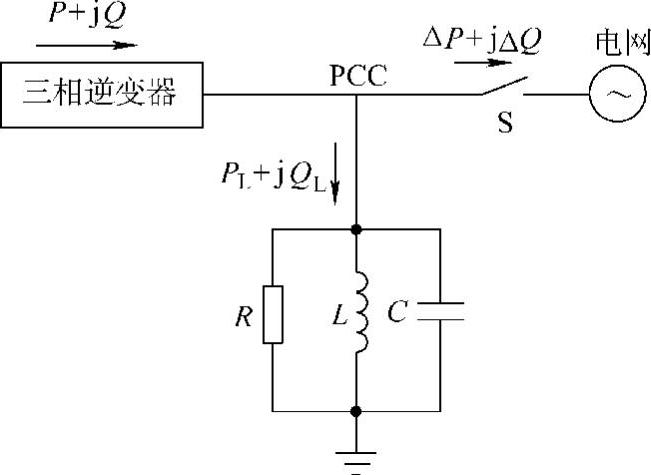
图8-40 孤岛检测电路原理图

5.主动负序分量扰动法

三相系统孤岛检测有其特殊之处，比如三相系统含有负序分量和零序分量，而单相系统中不存在。根据三相系统中含有负序分量的特点，可采用主动负序分量扰动法ANSCD（Ac-tive negative sequence component disturbance）进行孤岛检测。图8-40为孤岛检测电路的原理图。其中，并网逆变器输出端连接电网于公共耦合点PCC，负载采用RLC并联形式，通过切断开关S来模拟孤岛的发生。三相并网逆变器dq轴控制模型如图8-41所示。

图8-41 三相并网逆变器dq轴控制模型

在dq轴加入扰动量式（8-48）后，可得并网逆变器参考电流如式（8-49）所示。

经过坐标变换可得abc坐标系参考电流为

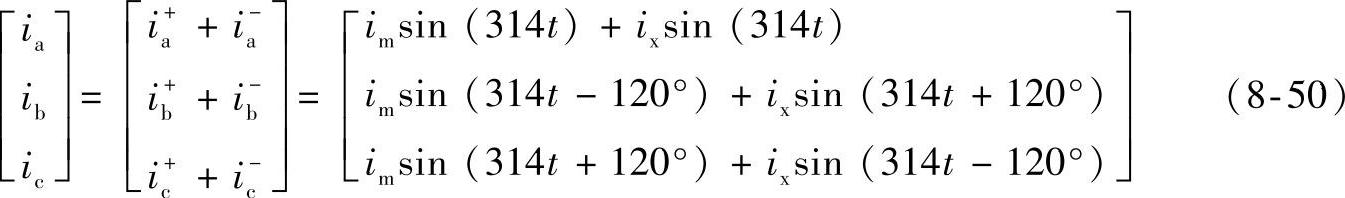
三相逆变器并网运行时，公共耦合点PCC电压为电网电压，理想情况下为

切断S电网断电，孤岛发生后，PCC电压为

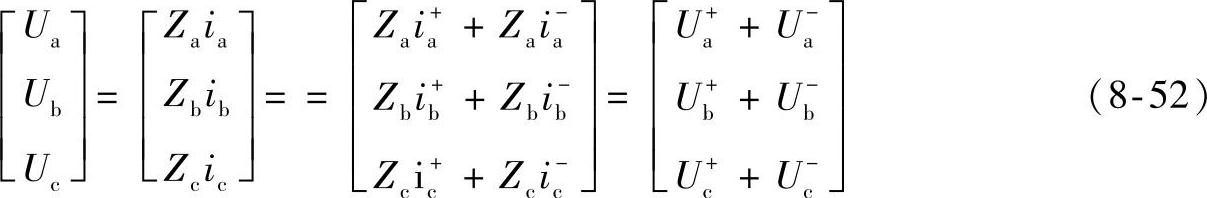
因此，加入有源负序电流扰动后，可以通过检测电压负序分量来判断孤岛的发生。

判断孤岛的关键之一在于提取PCC电压负序分量。根据对称分量法可知，三相电压矢量U_abc=[U_aU_bU_c]^T可分解为正序、负序和零序。其中，正序分量为

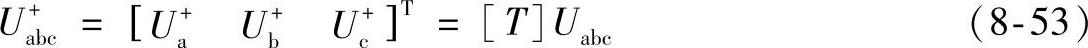
αβ坐标系电压矢量为

式（8-53）～式（8-56）联立可得αβ坐标系电压正序分量：

αβ坐标系电压负序分量为

式（8-57）、式（8-58）中，q为旋转因子，表示相移90°。采用G（s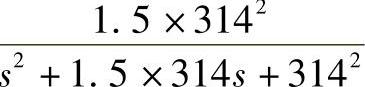）=实现q，其伯德图如图8-42所示。从图中可以看出，在正序和负序频率50Hz附近G（s）幅频特性为1pu，相频特性为-90°，满足q要求。

正序和负序分量提取之后需要确定其幅值和频率。可采用锁相环提取PCC电压正序分量和负序分量的幅值和频率信息。

三相电压不平衡度ε为负序分量与正序分量的百分比，即

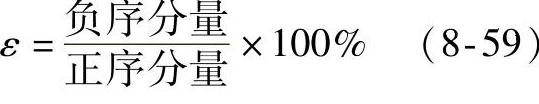
GB/T 15543—2008规定电力系统公共耦合点PCC正常工作电压不平衡度允许值为2%，短时不超过4%。因此，电网电压正常情况下电压不平衡度小于4%。下面设置有源负序电流扰动量为额定正序电流的4%，PCC电压负序分量上限值为正序分量的4%。一旦电网断电，若三相并联RLC负载平衡，则根据式（8-66）可知PCC电压负序分量增加至4%，达到上限值，从而检测到孤岛的发生。

图8-42 G（s）伯德图

电流控制存在误差将影响孤岛检测的有效性。传统基于同步旋转坐标系的PI控制对负序分量难以实现理想的控制效果，存在稳态误差。采用正序、负序双同步旋转坐标系PI控制方案可实现正序和负序分量的零稳态误差控制。然而其结构复杂计算量大。为了解决该问题，借鉴内模控制思想对负序分量进行控制。

内模原理指出：若要求一个反馈控制系统具有良好的跟踪指令以及抵消扰动影响的能力，并且这种对误差的调节过程结构是稳定的，则在反馈控制环路内部必须包含一个描述外部输入信号指令信号和扰动信号动力学特性的数学模型，该数学模型就是所谓的“内模”（internal model）。由于同步旋转坐标系下正序分量为直流量，其（标幺值）内模为，因此PI可以实现正序分量的零稳态误差控制。同理，同步旋转坐标系下负序分量为交流量，其频率为基波频率ω的2倍，其内模为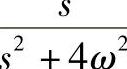。因此，根据内模原理可得正序、负序电流控制器如下：

下面对有源负序分量扰动法进行仿真分析，根据IEEE Std.929-2000标准中定义的最恶劣情况（worst case）进行验证。具体参数如下：三相电网电压380V/50Hz，逆变器额定功率3kW，直流母线电压800V，并网接口电感5mH，开关频率10kHz，并联RLC负载额定功率3kW（R=48Ω，L=61.1mH，C=165.87F），仿真结果如图8-43所示。

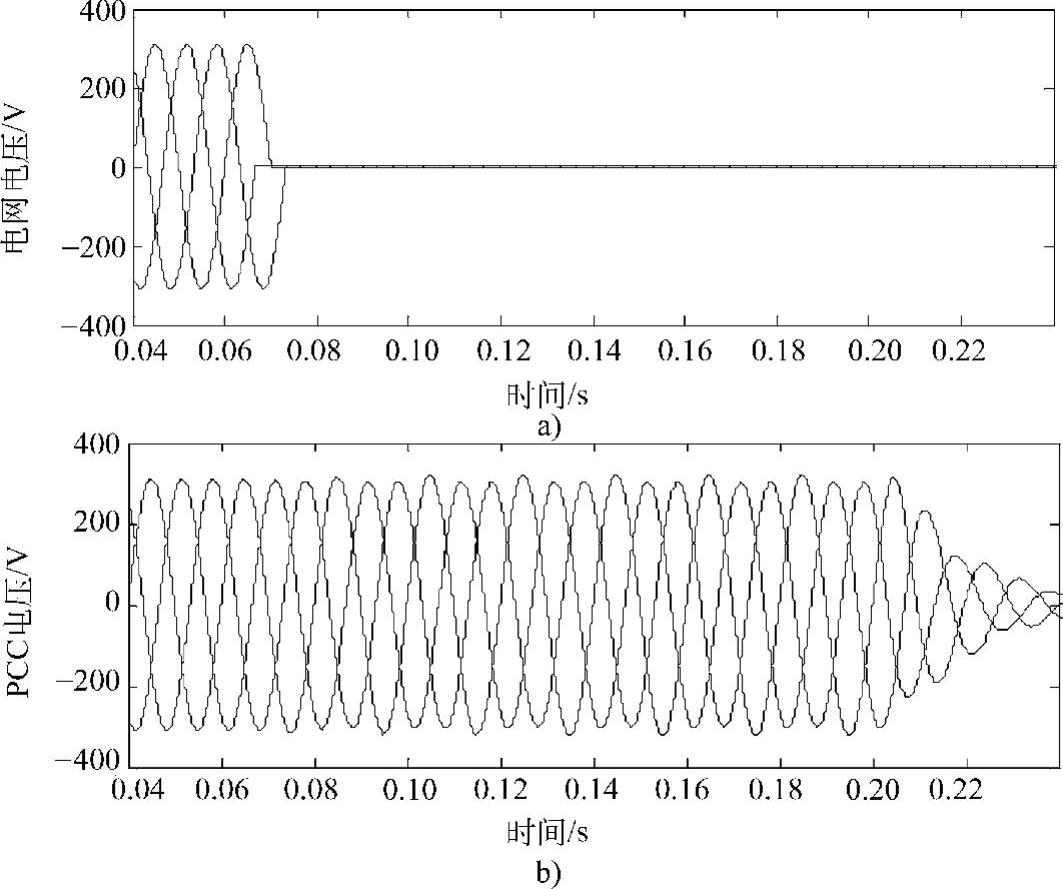
图8-43 仿真结果

a）电网电压 b）公共耦合点PCC电压

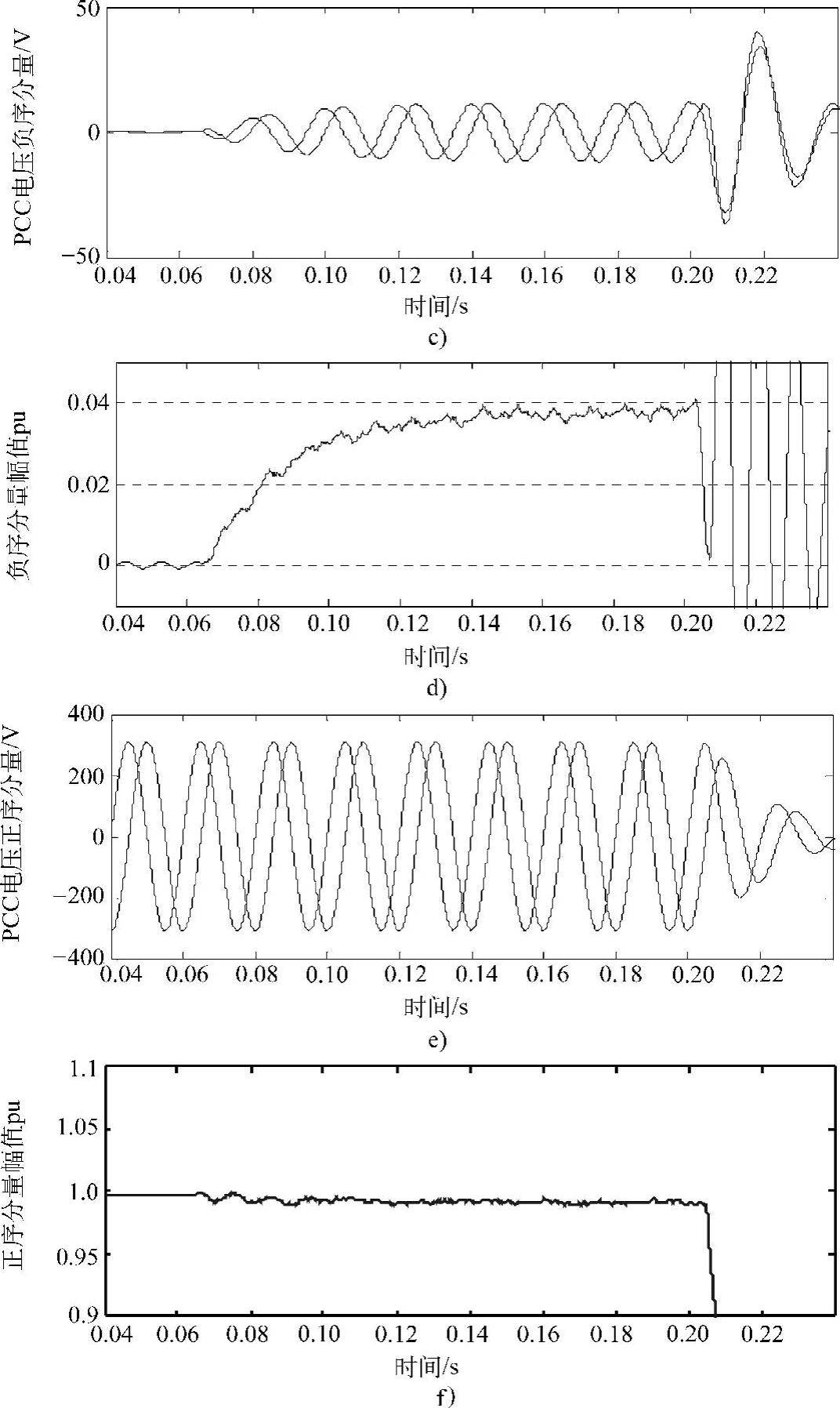
图8-43 仿真结果（续）

c）PCC电压负序分量U_α-_β d）PCC电压负序分量幅值 e）PCC电压正序分量U_α⁺β f）PCC电压正序分量幅值

下面说明图8-43各分图。图8-43a为电网电压波形，图8-43b为公共耦合点PCC电压波形。仿真中设置0.065s时电网断电，电网电压为0。其后并网逆变器仍向负载供电，此时PCC电压出现不平衡，三相逆变器输出电流中的负序分量导致PCC电压中同样含有负序分量，从而造成PCC三相电压不平衡。图8-43e～f提取的PCC电压正序分量信息。可以看出，0.065s孤岛前后正序分量基本不变。该现象可由式（8-52）和IEEE Std.929-2000的测试标准解释：并网逆变器输出正序功率和负载功率匹配。图8-43c为提取的PCC电压负序分量U_α-_β波形，说明孤岛后PCC电压中出现负序分量。图8-43d为提取的负序分量幅值。由于负序电流的扰动导致负序分量明显上升，在0.203s左右幅值增至额定正序电压的4%，达到上限值，从而检测到孤岛的发生，三相逆变器停止工作，实现孤岛保护，如图8-43g所示。根据以上仿真结果可知，在IEEE Std.929-2000标准中定义的最恶劣情况下，有源负序分量扰动法ANSCD仍可以检测到孤岛的发生，检测时间为（0.203-0.065）s=0.138s，远低于IEEE Std.929-2000标准中规定2.0s的标准。