模糊控制是采用模糊数学语言描述控制规则再通过计算机来操纵系统工作的一种非线性控制方式，属于智能控制的范畴。模糊控制与经典控制理论有着本质的不同，其核心在于对已知的对系统粗略的知识运用来描述系统，并在此基础上引入模糊控制算法。该方法有3个特点：一是不用数学方程而是用语言为代表的模糊变量描述系统；二是用条件命题语言记述模糊变量间的关系；三是用模糊推理方法实现系统的运算。采用模糊控制构建的控制系统具有如下特点：①模糊控制不依赖被控对象的精确数学模型，特别适宜对参数时变和非线性与不确定性的复杂系统或过程的控制。②模糊控制中的知识表示、模糊规则和合成推理是基于专家知识或操作者的成熟经验，并通过学习可不断更新。③模糊控制抗干扰能力强，响应速度快，并对系统参数的变化有较强的鲁棒性。模糊控制系统的基本结构与原理如图6-43所示。

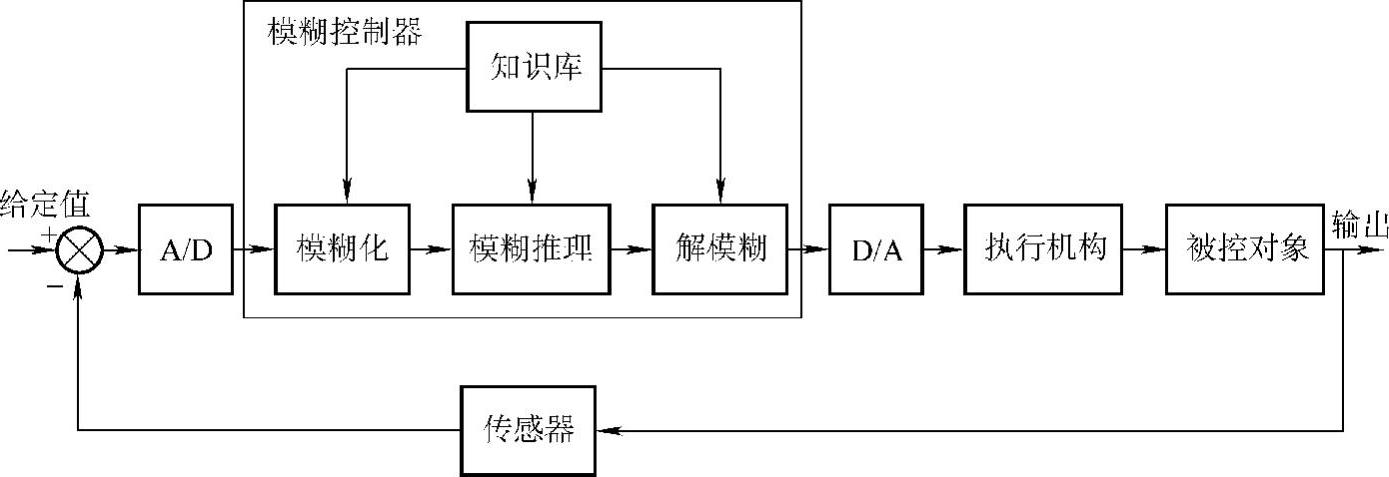
图6-43 模糊控制系统基本结构与原理框图

从图中可见，模糊控制系统一般由模糊控制器、输入输出接口装置、被控对象、执行机构和传感器5部分组成。

模糊控制器是模糊控制系统的核心，一个模糊控制系统的性能优劣，主要取决于模糊控制器的结构，所采用的模糊规则，合成推理算法以及模糊决策的方法等因素。模糊控制器通常由计算机实现，计算机通过采样获取被控制量的精确值，然后将此反馈值与给定值比较得到误差信号E（在此取单位反馈）。一般误差信号E作为模糊控制器的输入量，把误差信号E的精确量进行模糊化变成模糊量，误差E的模糊量可用相应的模糊语言表示。至此，得到了误差E的模糊语言集合的一个子集e（e实际上是一个模糊向量）。再由e和模糊控制规则R根据推理合成规则进行决策，得到模糊控制量u。u同样为一个模糊量，为了对被控对象施加精确的控制，还需将模糊量u转换为精确量，即在图中称为非模糊化处理（去模糊化），得到了精确的数字控制量后，再通过执行机构施加给被控对象。

模糊控制器的结构设计是指确定模糊控制器的输入变量和输出变量。模糊控制器的控制规则一般是根据专家控制规则提出的，而在控制过程中，人所能获取的信息量基本为3个，即误差、误差的变化及误差变化的变化量，因此模糊控制器的输入变量一般也取这3个。

模糊控制器输入变量的个数称为模糊控制的维数。一维模糊控制器只以误差为输入变量，很难反映过程的动态特性品质，它通常用于一阶被控对象，其动态性能不佳。三维模糊控制器从理论上讲控制精度较高，但模糊控制规则过于复杂，算法实现困难。以误差和误差的变化作为输入变量的二维模糊控制器，由于能够较严格地反映受控过程中输出变量的动态特性，而控制规则和算法又相对简单，因此这类结构的模糊控制器目前被广泛采用。本课题模糊控制器选择误差、误差的变化作为输入的二维结构。

模糊控制器的输出变量可按两种方式给出。一种是输出量即为直接的控制量（绝对式），另一种则是控制量的变化（增量式）。目前一般采用增量式，但有的系统中也将两种方式结合起来，如在误差大时以绝对的控制量输出，而误差小时以控制量的增量输出，通过这种方法可获得较好的上升特性，改善了控制器的动态品质，但模糊控制器的结构及控制算法相对复杂。

在模糊控制的实际应用中，隶属函数形状和它在模糊子集论域内的分布状况，对模糊控制规则的完备性及模糊控制的互作用性产生重要的影响，从而对控制效果发生作用。常见的隶属函数有三角形、梯形、高斯形、双高斯形、S差形、钟形等。其中三角形隶属函数又分为均匀分布和非均匀分布两种。隶属函数的作用可归结为

（1）隶属函数的形状对系统的稳定性和快速性有一定影响。采用三角形和高斯型隶属函数时系统控制性能很接近，而梯形隶属函数的控制性能则比前两者稍差，特别表现为超调量和稳态误差较大，系统振荡加剧。一般而言，隶属函数的形状越陡，系统分辨率就越高，控制灵敏度也较高；相反，若隶属函数形状较缓，则控制特性也较平缓，系统的稳定性较好。因此，在选择模糊变量的隶属函数时，在误差较小的区域，可采用分辨率高的隶属函数，使系统具有较好的灵敏度；在误差较大的论域，采用分辨率较低的隶属函数，使系统具有良好的鲁棒性。

（2）当三角形隶属函数为非均匀分布时，对比均匀分布方式，系统稳态误差较小，响应更灵敏，曲线上升速度快。由于三角形隶属函数计算比较简单，控制系统的实时性比曲线形隶属函数要好，且采用非均匀分布时可以减小系统静差，提高响应速度，因此在实际控制系统中被广泛采用。

由计算机实现模糊控制算法时，逆变器每个开关周期A/D采样得到的被控制量需经计算机计算，得到模糊控制器的输入变量即误差E及误差变化EC。为了进行模糊化处理，必须将输入变量从基本论域转换到相应的模糊集论域，从而引出量化因子K_e和K_ec的概念。而经模糊控制算法给出的控制量（精确量），还不能直接控制对象，需将其转换到为控制对象所能接受的基本论域中去，所以又引出控制量比例因子K_u。

量化因子K_e、K_ec和比例因子K_u对控制系统的动静态性能有很大的影响，例如对于一个阶跃给定信号对系统响应分析可归结如下：

（1）当K_e增大时，相当于缩小了误差的基本论域，增大了误差变量的控制作用，因此使得系统上升时间变短，但K_e过大时会出现超调，并使得系统的过渡过程变长，严重时甚至使系统产生振荡；若K_e较小，则系统上升较慢，快速性差，同时稳态误差较大。

（2）K_ec选择较大时，提高了模糊控制器的灵敏度，能有效地抑制超调，但系统的响应速度变慢；K_ec较小时则会产生较大的超调和振荡。K_ec对超调的影响十分明显。量化因子K_e和K_ec的大小意味着对输入变量误差和误差变化的不同加权程度，二者之间也相互影响。

（3）输出比例因子K_u作为模糊控制器的输出增益，它的大小直接影响着控制器的输出和模糊控制系统的特性。K_u在系统响应的上升和稳定阶段对控制性能有不同影响。在上升阶段，K_u选择越大系统动态响应越快，但容易导致系统超调；在稳定阶段，K_u过大会引起振荡。K_u较小对系统稳定有利，但将延长响应时间。

另外，量化因子和比例因子的选择并不是唯一的，可能有几组不同的值，都能使系统获得较好的响应特性。对于比较复杂的被控过程，有时采用一组固定的量化因子和比例因子难以收到预期的控制效果，可以在控制过程中采用改变量化因子和比例因子的方法来优化控制性能，对此将有进一步研究。

模糊控制器的核心是“If…Then…”形式的模糊控制规则，控制规则的选取直接关系到系统控制性能的优劣，是模糊控制器设计的关键。模糊控制规则通常是总结专家经验或经反复实验试凑、修改确定。目前模糊推理大概有几十种方法，其中常用的有MAX-MIN合成法、拉森乘积运算法和Sugeno型推理方法3种。其中Sugeno型推理方法适合隶属度为单调的情况；而MAX-MIN合成法直接采用极大极小运算，计算比较简单，因此在模糊控制系统中应用最为广泛。

下面给出一组实例。模糊控制器采用PI型二维结构，输入变量为误差E（K）、误差变化量EC（K）=E（K）-E（K-1），输出量为控制量增量U（K）=Δu。其中E、EC和U的模糊子集均定义为{NB，NM，NS，ZE，PS，PM，PB}，论域为[-8，+8]。

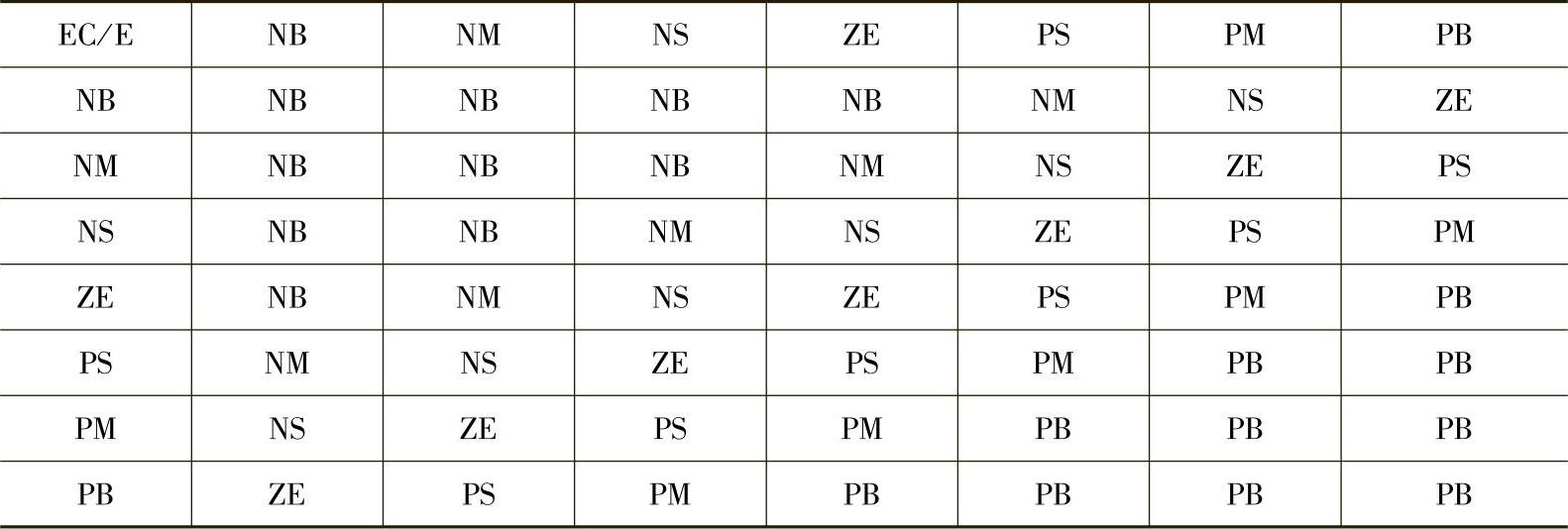
如图6-44所示，E和EC的隶属度函数采用对称三角形非均匀分布，U的隶属度函数采用对称三角形的均匀分布。主模糊控制器的模糊控制规则见表6-1所示。

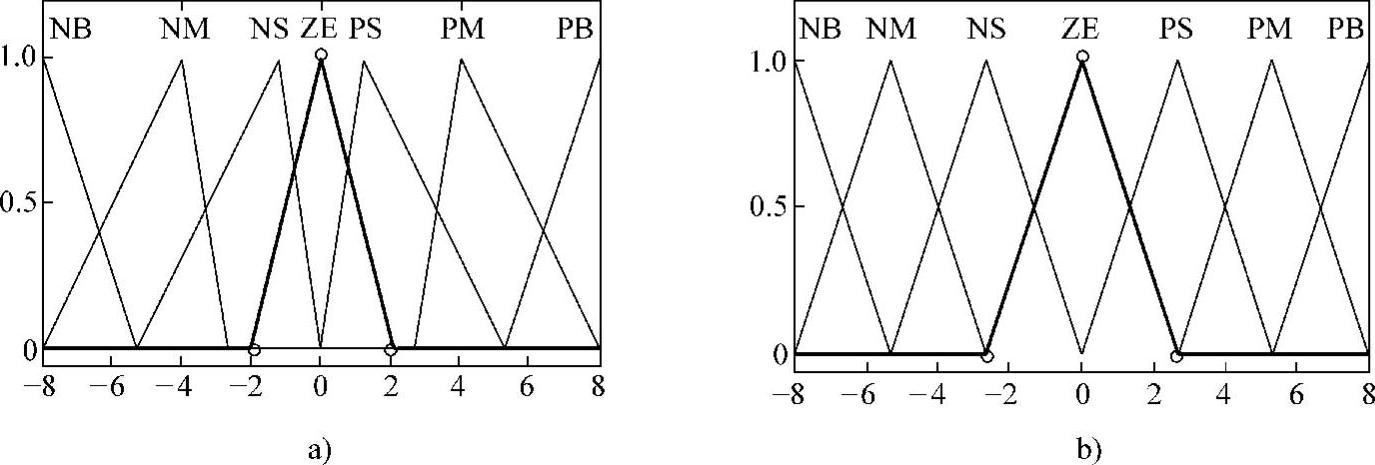
图6-44 隶属度函数

a）E和EC的隶属度函数 b）U的隶属度函数

表6-1 主模糊控制器模糊控制规则表

解模糊的目的是将模糊推理得到的模糊控制量转化为执行机构所能接受的精确量，但解模糊过程目前尚无系统的方法，以下就常用的几种方法作一比较：(www.daowen.com)

1）最大隶属度法

这种方法直接选取模糊子集中隶属度最大的元素作为控制量，例如模糊子集为C，所选择的隶属度最大的元素u应满足：

μC（u）≥μC（u），u∈U（6-130）若输出量的隶属度函数有多个极值，则取它们的平均值为控制量。

最大隶属度法的优点是方法简单、易行，算法实时性好，能够突出主要信息的控制作用，但对于隶属度较小元素的控制作用没有考虑，利用的信息量少，因此比较粗糙，一般用于控制性能要求不高的系统中。

2）取中位数法

选取将模糊子集的隶属曲线和横坐标所围成区域的面积平分为两部分的点，即将模糊集中位数作为控制量。该法比较充分地利用了模糊子集提供的信息，但计算比较复杂，在连续隶属函数时需要求解积分方程，而且缺乏对隶属度较大元素提供主导信息的充分重视，因此该法在实际应用中受到一定限制。

3）加权平均法

如式（6-131）所示，加权平均法针对论域中的每一个元素u_i（i=1～n），以它作为判决输出模糊集合的隶属度μ的加权系数，则平均值u就是模糊集合求得的判决结果。

有研究表明，使用取中位数法的模糊控制器类似于多级继电器控制，加权平均法则类似于PI控制器。一般而言，加权平均法比取中位数法具有更好的静态性能，动态性能则略逊于取中位数法，而两种方法都优于最大隶属度法。

PID控制中的比例增益K_P、积分增益K_I和微分增益K_D均为常数，一旦控制器设计好以后，在控制过程中不再改变，因此PID控制属于线性定常控制。

模糊控制本质上为非线性控制，但是其输入变量也包括e和edt（ec），输出变量也有u（位置式输出）和Δu（增量式输出）两种形式，与PID控制的输入输出变量完全相同。类比传统的PD、PI和PID控制，可将模糊控制器分为以下3种类型。

1）PD型模糊控制器

其输入为e和ec，输出为u，模糊控制器的功能可看做是一个非线性函数：

u=f（e，ec）（6-132）

PD型模糊控制器响应快，超调较小，但缺点是存在系统静差。

2）PI型模糊控制器

其输入为e和ec，但输出为控制量的增量Δu，模糊控制器可表示为

Δ_u=f（e，ec）（6-133）

此时模糊控制器与常规PI控制器类似，称为PI型模糊控制器。PI型模糊控制器由于引入了积分作用，因此减小了系统静差，但缺点是系统响应较慢，上升时间长，系统易振荡，调整时间较长。

3）PID型模糊控制器

PID型模糊控制器一般可由两种方式实现：一种是由一个常规PI控制器（或PI型模糊控制器）和一个二维PD型模糊控制器（或常规PD控制器）并联组成，两个控制器的输出叠加作为模糊PID控制器的总输出。

另一种在二维PD型模糊控制器的基础上，对误差e的模糊值进行积分，将积分值叠加到输出控制量上。而实际上采用三维结构的模糊控制器也相当于一个PID型模糊控制器。

PID型模糊控制器从理论上讲能够综合PI和PD型模糊控制器的优点，避免系统稳态误差的产生，并提高系统动态响应速度。但由于控制规则和参数增多，使得其设计复杂化，并产生极限环、振荡和稳定性等问题，因此在实际应用中主要还是以PD或PI型模糊控制器为主。

考虑到输出波形稳态精度的要求，逆变器模糊控制器的输出类型选为PI型，也即控制算法输出为占空比的增量。