最优控制问题就是寻找一个控制系统的最优控制方案或最优控制规律，使系统以最佳的性能达到预期目标。最优控制理论中的无限时间状态调节问题在线性二次调节器中占有重要的地位，并有广泛的实际应用价值。对于控制精度要求较高的系统，采用最优控制的原则，会有明显的效果。最优控制是研究和解决从一切可能的控制方案中寻找最优解的一门学科。它是现代控制理论的重要组成部分。线性二次型最优控制问题简称为LQ（Linear Quadratic）问题。所谓LQ最优控制就是寻找一个控制量u*（·），使得系统沿着由指定初始状态x₀出发的相应轨线x*（·），满足制定的性能指标函数：

式中，控制函数u*（·）为LQ问题的最优控制，x*（·）为相应的最优轨线，J（u*（·））为最优性能值。从数学上看，LQ最优控制实质上就是求条件极值问题。线性二次型控制应用状态反馈实现，具有比例负反馈的形式，这对于消除系统静差式不利的。通过对数学模型的转换构造新的系统形式，保证系统最终控制实现中含有积分环节，以利于消除静差。并网情况下，以电网流出电流为正方向，三相电压型可逆变流器dq旋转坐标系系统的数学模型为

将模型进行整理：

式中，A和B分别为2×2和2×2常数阵，x为二维状态，u为二维输入。这里：

为引入积分量，进行如下变换：

式中x_s、u_s为稳态工作点。则：

将系统进行扩展：

式中

I₂为二阶单位矩阵。且有

k_23k14^-k24k13≠0（6-109）

设(www.daowen.com)

则

而

式中，A和B分别为4×4和4×2的常数矩阵，X为四维的状态变量，u为二维的输入变量，并且

对这个系统新的系统状态方程进行优化控制的设计。设目标函数为

式中，Q为4×4正定或半正定对称常数矩阵（系统已满足可观测条件），R为2×2正定对称常数矩阵。应用最优控制，要使目标函数为最小的最优控制量为

则

式中，P是黎卡提方程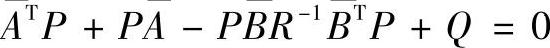的正定对称解，K₁为2×2的常数矩阵。将式（6-115）展开可得

则

系统控制量为

式中，i_d*和i_q*分别有功电流和无功电流的期望值，i_d*由输出电压经调节器给定，单位功率因数控制时i_q*=0。