PI控制器在电网基波频率处的增益为有限值。系统存在稳态跟踪误差。比例谐振（PR）控制器的传递函数为

PR控制器在基波频率处的增益为

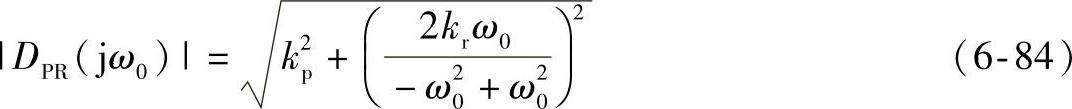
可见，PR控制器在基波频率处的增益趋近于无穷大，可以实现对某一固定频率正弦指令信号的无静差跟踪控制。而逆变器并网运行时，要求控制逆变器的输出电流为与电网电压频率和相位一致的标准正弦电流，以实现单位功率因数并网发电。因此，PR控制器适合于逆变器并网电流的控制。将其应用于逆变器并网控制时，系统闭环传函ϕ（s）在基波频率ω₀处的增益ϕ（jω₀）趋近于1，而电网电压扰动量对输出的传递函数ϕ_N在ω₀处的增益ϕ_N（jω₀）趋近于0，从而使输出电流可以完全跟踪给定正弦电流，实现零稳态误差；并且可以克服电网基波电压扰动的影响。因此，在并网逆变系统中，PR控制器与PI控制器相比，具有更好的稳态性能和抗扰性能。

在实际系统中，由于理想的PR控制器难以实现，可以采用一种容易实现的准PR控制器，其传递函数如下所示。

由式（6-85）可知，准PR控制器有3个控制参数k_p、k_r和ω_c，这3个控制参数决定系统的性能，因此，需要对其进行优化设计。

将准PR控制器应用于并网电流控制时，其中，ω₀为工频角频率，即ω₀=314rad/s。在准PR控制器参数设计过程中，为了便于分析，设其中任意两个参数不变，然后观察第3个参数变化对系统性能的影响。

首先，设k_p=0，ω_c=1，而k_r变化。此时式（6-85）的频率特性如图6-30所示。k_r只影响控制器的增益，而不影响控制器的带宽。控制器的增益和k_r成正比，k_r越大增益越大，稳态误差越小。但是过大的k_r会使谐波分量放大，降低并网电流质量，只要保证在基波频率附近具有足够的增益，而在远离基波频率处应该具有一定的衰减作用。

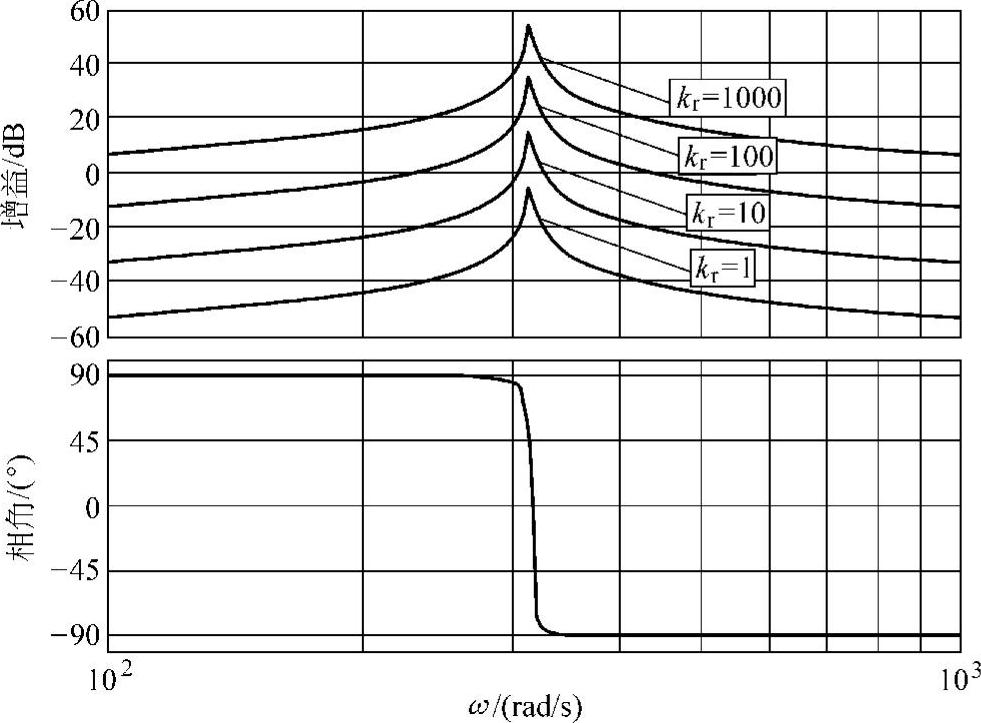
图6-30 k_r变化下准PR控制器伯德图

其次，设k_p=0，k_r=1，而ω_c变化时，其频率特性如图6-31所示，ω_c不仅影响控制器的带宽，还影响控制器的增益。随着ω_c的增加，控制器的带宽和非基波频率处的增益都增大（基波频率处的增益不变）。设k_p=0，将s=jω代入式（6-85），则有

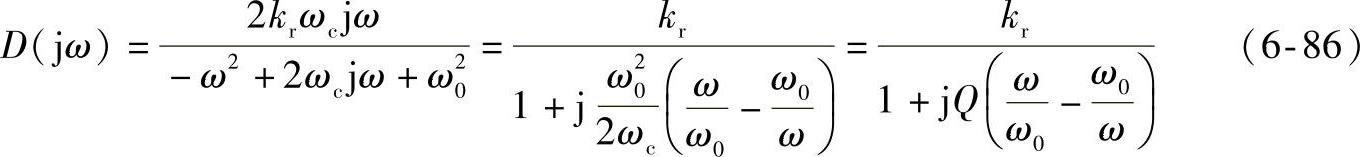
式中。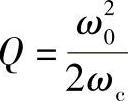

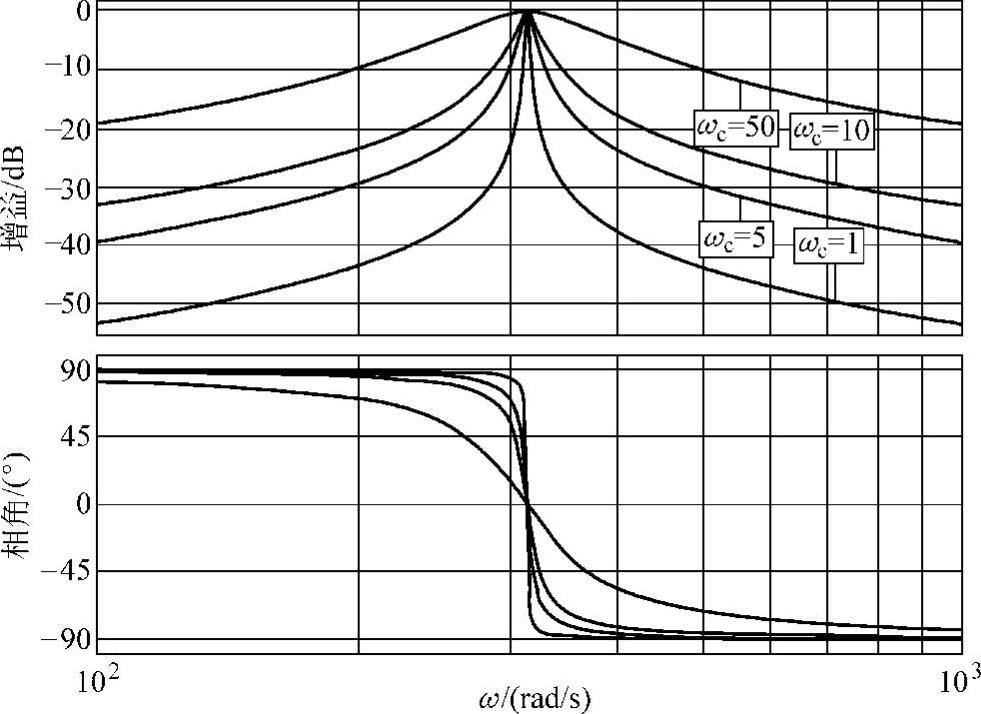
图6-31 ω_c变化下准PR控制器伯德图(www.daowen.com)

根据带宽的定义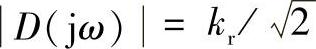，时对应的两个频率差即为带宽。因此，利用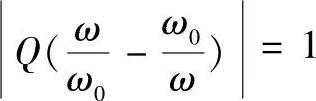，经过计算可以得到控制器的带宽为

设电网频率允许波动范围为±0.8Hz，则控制器带宽应为BW=1.6Hz，即有ω_c=5rad/s。

为了研究控制器的抗扰性能，定义谐波阻抗为电网谐波电压与引起的系统输出谐波电流之比。谐波阻抗越大，引起的输出谐波电流越小，系统的抗扰性能越好。并忽略由于开关动作产生的小惯性环节对系统的影响，可以获得系统的谐波阻抗为

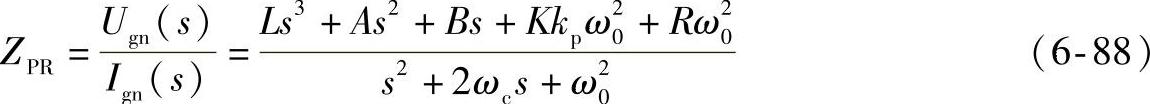
式中，A=Kk_p+2Lω_c+R，B=Lω²₀+2Kk_pω_c+2Rω_c+2Kk_rω_c；U_gn（s）、I_gn（s）分别为电网n次谐波电压和由此产生的n次谐波电流的拉氏变换。

最后，设ω_c=5rad/s，k_r=100，k_p变化，逆变器参数为L=3mH，R=1Ω，K=96，此时系统的谐波阻抗如图6-32所示。由图6-38可知，系统谐波阻抗受k_p的影响较大，随着k_p的增加，系统的谐波阻抗增大，系统抗扰性能越好，但是k_p过大将会使系统不稳定。

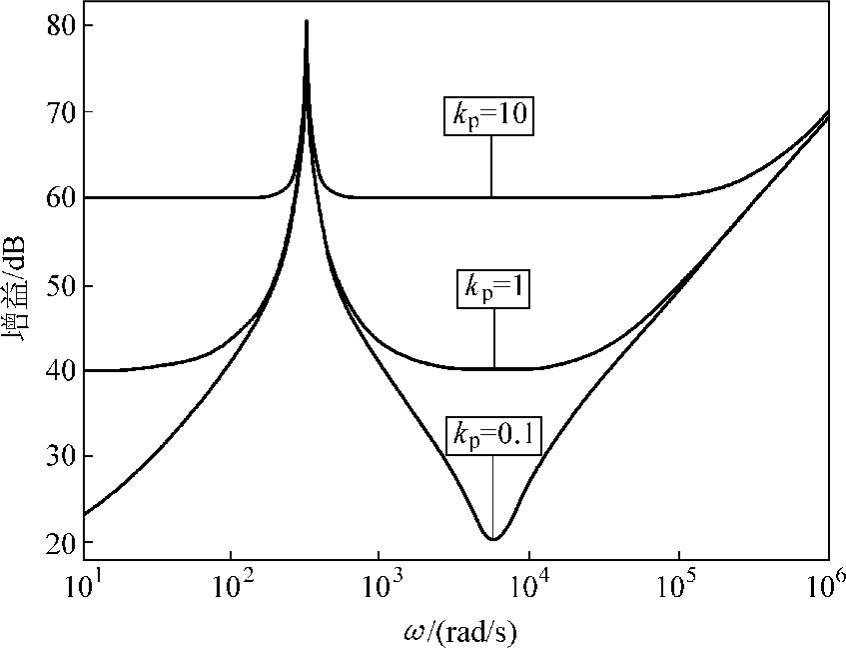
图6-32 并网逆变系统的谐波阻抗

在比例积分调节器G（s）的作用下，假设直流母线与占空比的组合增益为大，忽略电网电压扰动和小惯性环节，可以得到系统闭环传递函数

设ω_c=5rad/s，k_r=100，k_p从1～10变化，可以绘出闭环系统的根轨迹如图6-33所示。为了便于分析，系统根轨迹中忽略了远离虚轴的非主导极点。由图6-33可见，当k_p太大或太小时，系统的主导极点趋近虚轴，使系统稳定裕度变小，稳定性变差。因此，设计k_p时要综合考虑系统的稳定性和系统的抗扰性能。

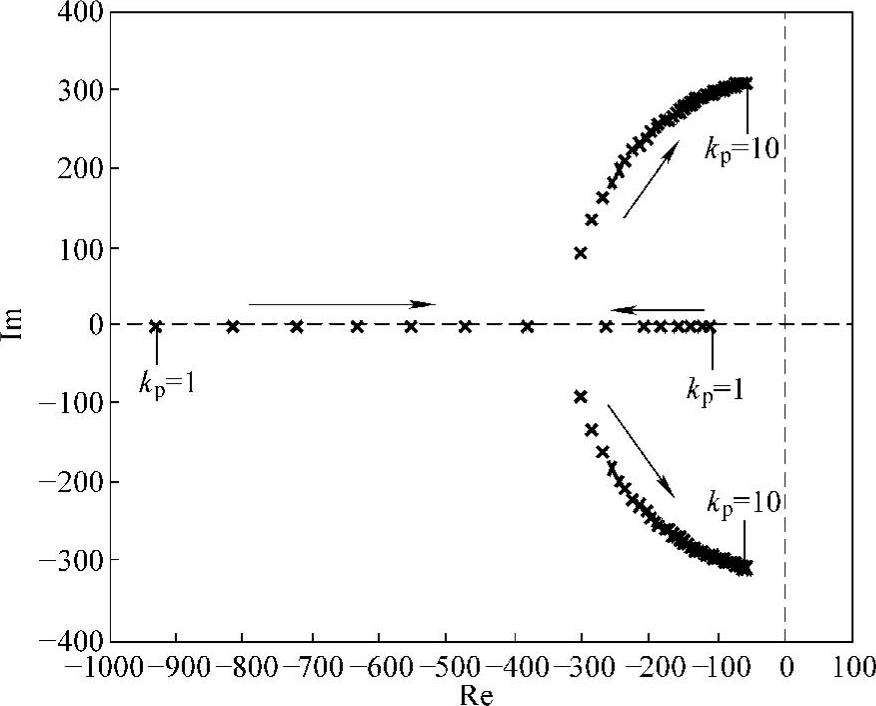
图6-33 系统的根轨迹

综上所述，准比例谐振（PR）控制器参数的设计步骤可以归纳如下：根据系统需要的带宽选择ω_c；根据系统需要的增益选择k_r；根据谐波阻抗，设计k_p使系统稳态性能和抗扰性能满足要求。