IMC的系统结构如图6-25所示。图中，p为对象模型；p～是p的基准模型；q是IMC控制器；u是控制器的输出；控制目标是输出y跟踪给定输入r。虚线所包括的这部分除了控制器q以外，还显式地包含模型p～，因此这种反馈控制结构被称作内模控制（IMC）。

如果对控制器q进行等效变换，可变换为图6-26a所示图中的虚线所围部分。推导图6-26a的输入，根据输出关系可以看出两个模型p～互相抵消，即图6-26中a和b是等效的，由此可得到经典控制器C和内模控制器q的关系：

图6-25 IMC系统结构图

通过以上变换得到的经典控制器具有内模控制器的特点：结构清晰、设计简单、具有良好的跟踪性能和抗外扰能力、能消除不可测干扰、鲁棒性强等优点。

图6-26 内模控制和经典控制的关系图

a）内模控制 b）经典控制

单相逆变器空载传递函数表达式：

其中自然振荡频率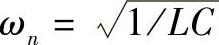，阻尼比。把负载电流看做干扰信号，则乘性模型不确定性函数l_m（s）为

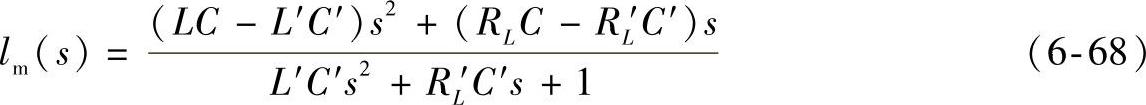
式中，L′、C′、R_L′分别为实际的电感、电容、阻尼电阻。并且考虑了输出滤波电感L，输出滤波电容C，阻尼电阻r的变化。把负载电流作为干扰信号，兼顾了逆变器的各种带载的情况，且内模控制有很强抗干扰能力，故把负载电流作为干扰信号是合理的。

由图6-25所示的IMC控制系统，可以容易地得到输入和输出之间的函数：

假定基准模型准确，则

Y（s）=P（s）Q（s）R（s）+（1-P（s）Q（s））D（s）（6-70）

从式（6-70）可以清楚地看到，无论是对于输入R（s）的响应，还是对于干扰D（s）的衰减，都与对象固有的极点有关。而逆变器空载数学模型G₀（S）可看出其等效阻尼电阻和阻尼比ξ都相当小，也就是说G₀（S）的极点离S域虚轴很近，故系统有很严重的振荡倾向，整流性负载时电压输出波形畸变率很高。在上述情况下内模控制对系统的动态性能几乎没有任何改善，故需要通过其他方式来改善系统的动态性能。以上分析可知逆变电源的空载特性之所以不好，最主要的原因是阻尼系数太小，因此，最直接有效的解决办法是增加控制对象的阻尼。下面利用极点配置法设计输出电压PD瞬时值反馈内环。系统控制如图6-27所示。

图6-27 带PD反馈内环的IMC-PID逆变器控制系统框图

选取电容电压u_c和电容电流i_c作为状态变量，通过状态反馈：kx=（k₁u_c+k₂i_c），如果期望的闭环极点为

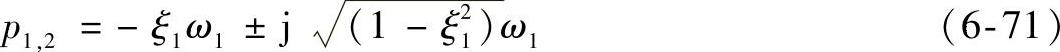(www.daowen.com)

式中 ξ₁——加了状态反馈后的系统期望的阻尼比；

ω₁——期望的自然振荡频率。

k₁=ω²₁LC-1、k₂=2ξ₁ω₁L-R_L分别为状态反馈系数k₁、k₂。

根据电容电流和电压的关系，将电容电流的反馈等效的转换为对电容电压微分的反馈，这样就不需要电容电流的检测设备，降低了逆变器成本。根据以上分析可得内环PD控制器参数为

内模控制器的设计方法有很多种，最常用的是零极点对消法，也称两步设计方法。

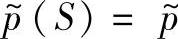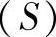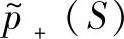（1）对控制对象的基准数学模型进行分解+-，包括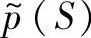中的滞后环节和极点在右半平面的部分，为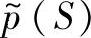中的最小相位部分。加了PD反馈内环后，逆变器的基准数学模型为

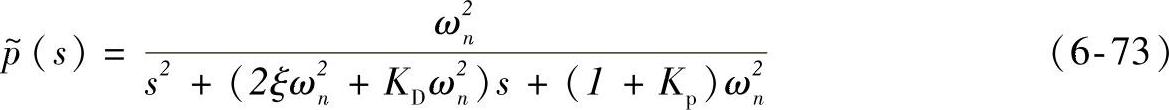
分解可得

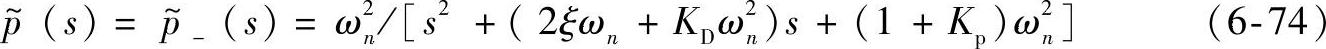
其中，。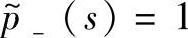

（2）求取内模控制器与经典反馈控制器。

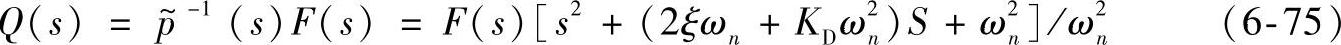
滤波器取Ⅰ型滤波器F（s）=1/（τs+1）。根据经典控制器c和内模控制器q的关系，则有

（3）将经典反馈控制器转换为传统的PID控制器。假定PID控制器结构为

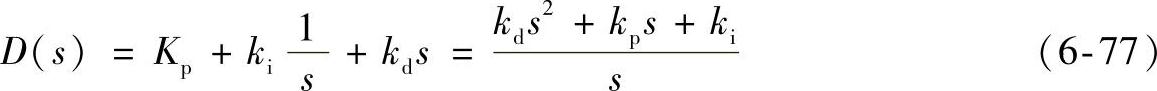
有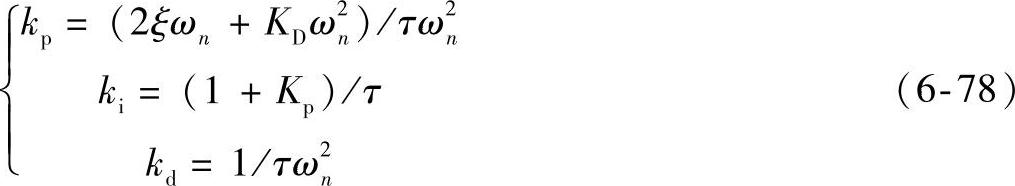

其中τ为整定滤波器参数。加了PD内环后，逆变器的基准数学模型如式（6-79）所示，模型的乘性不确定性函数l_m（S）为

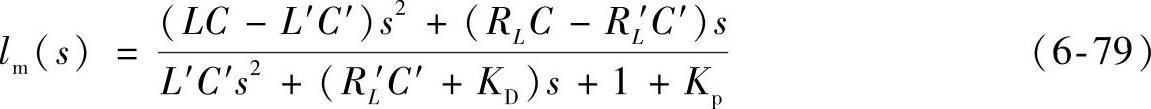
为了使设计的内模控制系统具有鲁棒稳定性，互补灵敏度函数_η（s）必须满足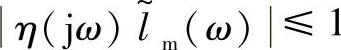：，首先确定模型不确定性函数的界l_m（ω），然后根据互补灵敏度函数_η（jω）确定τ。考虑0.5L≤L′≤1.5L，0.5C′≤1.5C，0.5r≤r′≤1.5r情况下不确定性函数的界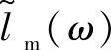。τ越小，系统的动、稳态性能越好，τ越大系统的鲁棒稳定性越好，为了得到良好的跟踪给定和抑制干扰的性能以及良好的鲁棒稳定性，τ的选取应该综合考虑这两个方面。