在工程实际中，应用最为广泛的调节控制规律为比例积分微分控制，简称PID控制。PID控制器结构简单、稳定性好、工作可靠、调整方便。PID调节器的微分方程数学模型为

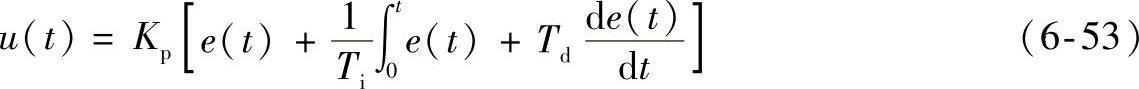
式中，u（t）为PID调节器的输出信号，这个信号就是送到被控对象的。系统误差信号定义为e（t）=r（t）-c（t），r（t）是系统的给定输入信号；c（t）是系统的被控量。PID调节的传递函数模型为

由上式可得PID调节的几种特例形式：①当T_d=0、T_i=∝时，则有G_c（s）=K_p，此为比例（P）调节器；②当T_i=∝时，则有G_c（s）=K_p[1+T_ds]，此为比例微分（PD）调节器，相当于超前校正；③当T_d=0时，则有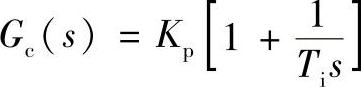，此为比例积分（PI）调节器，相当于滞后校正；当K_p≠0、T_d≠0、T_i≠∝时，则有G_c（s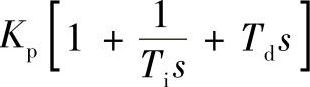）=，为全PID调节器。

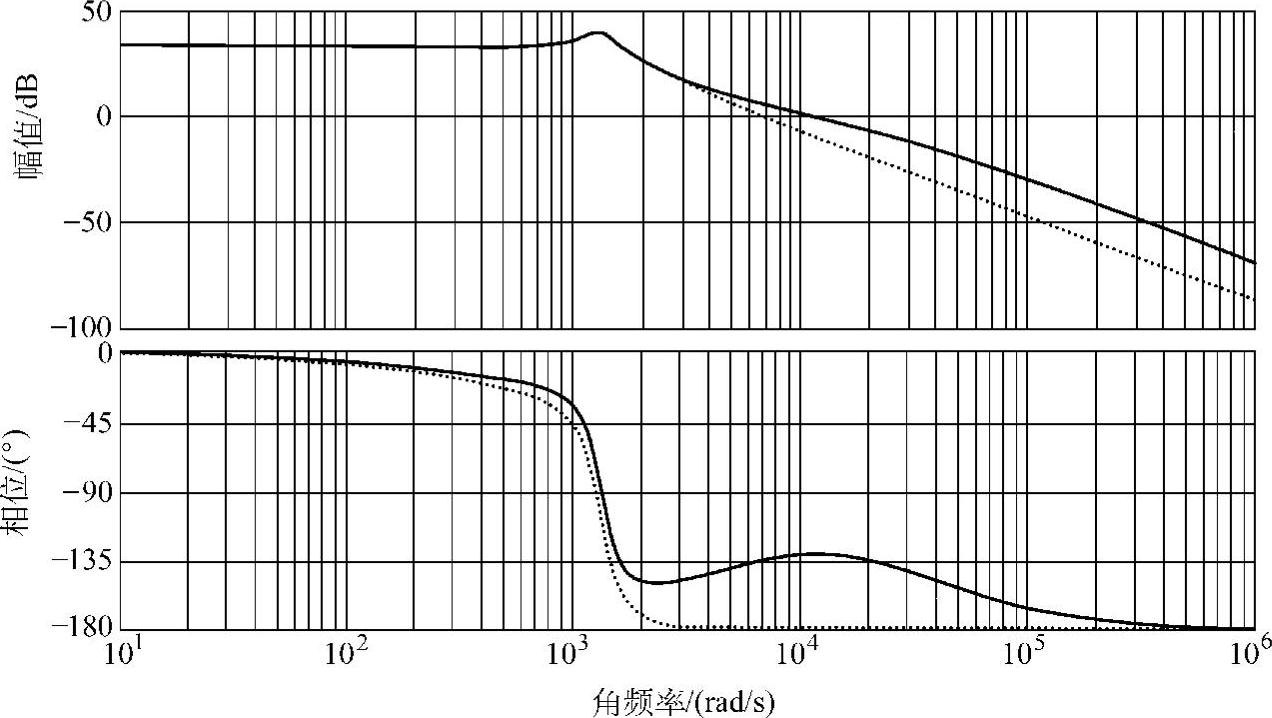
图6-18 系统校正前后的伯德图（虚线为校正前系统伯德图，实线为校正后系统伯德图）

PID控制是通过3个参量K_p、T_i、T_d起作用的。这3个参量取值的大小不同，就是比例、积分、微分作用强弱的变化。对于P调节器，随着K_p值的加大，闭环系统的超调量加大，系统响应速度加快。若K_p超过一定值，则系统会变得不稳定。对于PI调节器，随着T_i值的加大，闭环系统的超调量减小，系统响应速度略微变慢。对于PID调节器，由于微分环节的作用，在曲线的起始上升段呈现尖锐的波峰，之后曲线也呈衰减的振荡；保持K_p、K_i一定值不变，在一定范围内，随着T_d值的加大，闭环系统的超调量增大，但经过曲线尖锐的起始上升段后响应速度有所变慢。

电流环控制如图6-19所示。该电流控制方法是通过指令电流与反馈电流比较后得到电流误差信号，然后经过调节器获得调制信号，并与三角载波进行调制产生开关所需的PWM控制信号，从而控制逆变器输出电流。在该控制方式下，开关频率通常等于载波频率，输出电流的谐波含量较少。实际应用中大多数采用PI调节器。但是由于PI调节器中积分环节的存在，在跟踪正弦指令信号时会产生相位和幅值误差。

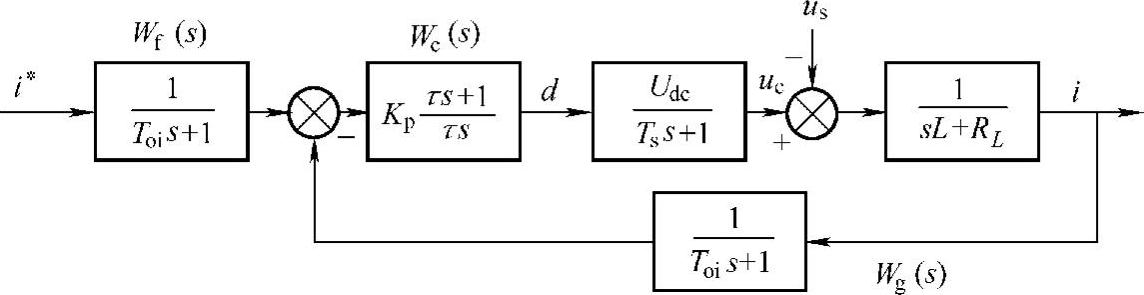
图6-19 并网逆变器三角波比较电流环控制框图

根据二阶工程设计法，优化的PI调节器为

考虑传感器及执行机构的时延后，按照典型I型系统设计电流环，T_oi为电流反馈滤波时间常数，T_s为电流内环采样周期，U_dc为逆变器等效增益，d为PI调节器输出占空比，u_c为桥臂电压，u_sd为输出电压。为了进一步简化调节器设计和抑制电流超调，增加了给定滤波环节W_f（s）。(www.daowen.com)

不考虑输出电压影响时，选择阻尼系数ζ=0.707，得到PI调节器的比例系数K_p与积分时间常数τ的计算公式为

式中，T∑i=T_oi+T_s，为小时间常数之和。

应用PI调节器实现单环电压输出控制的逆变器等效电路结构图如图6-20所示。

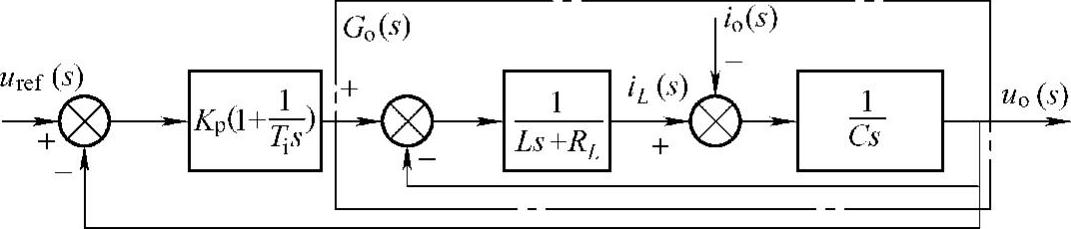
图6-20 电压单环控制结构图

忽略输出电压对系统电流的影响，或是采用输出电压前馈解耦，则逆变系统的结构如图6-21所示。

图6-21 逆变系统忽略电压影响的控制结构简图

按照典型系统的二阶工程设计法，可以得到PI调节器的积分时间常数和比例系数为

式（6-57）和式（6-58）中，h为中频宽。