1.基于αβγ坐标系的3DSVM

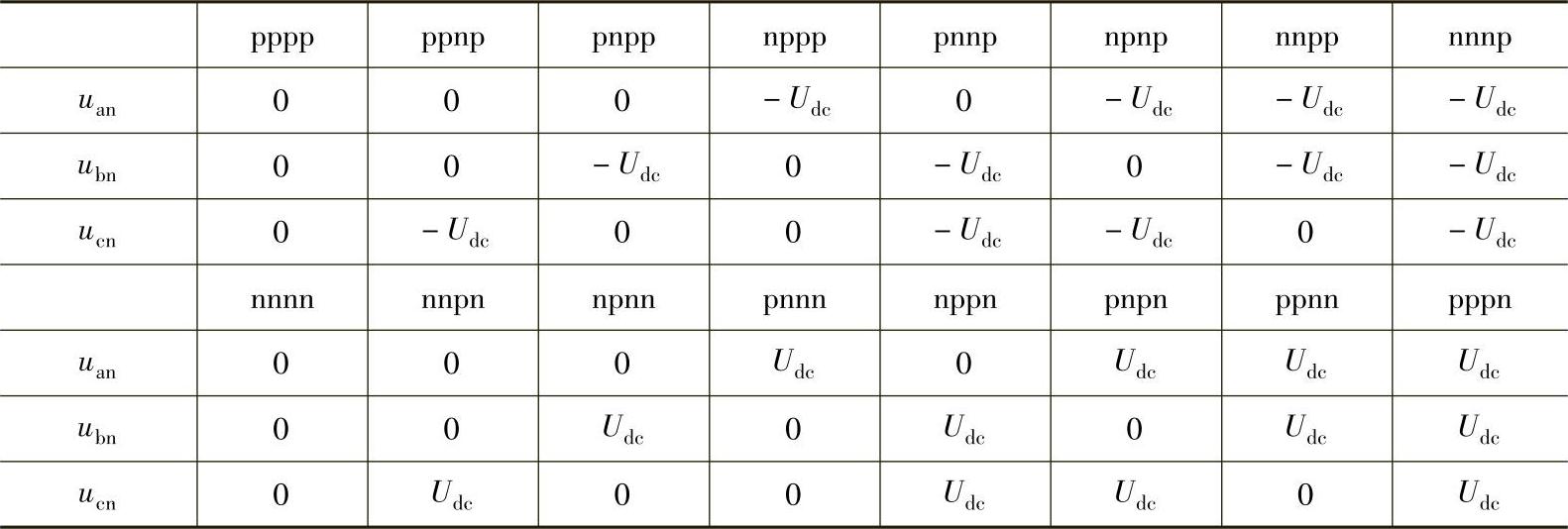
应用在三相四桥臂逆变器上的基于αβγ坐标系的3D SVM是传统2D SVM的拓展，两者的基本方法是一致的。在三相四桥臂逆变器中（见图4-14），由于第四桥臂的作用，三相输出电压可以独立控制。在四桥臂变换器中，共有2⁴=16种开关状态。为了方便说明，对开关状态作如下定义：设定某种状态为x_ax_bx_cx_n，x_i（i=a，b，c，n）从前至后依次表示第i桥臂开关情况。以a相桥臂为例，如果上桥臂导通下桥臂断开则有x_a=p（表示输出为正），反之则有x_a=n（表示输出为负）。依此类推，若开关状态为pppn，则表示该时刻a、b、c相桥臂上管导通下管断开，n相桥臂下管导通上管断开。得到的16种开关状态与输出相电压关系见表5-5。

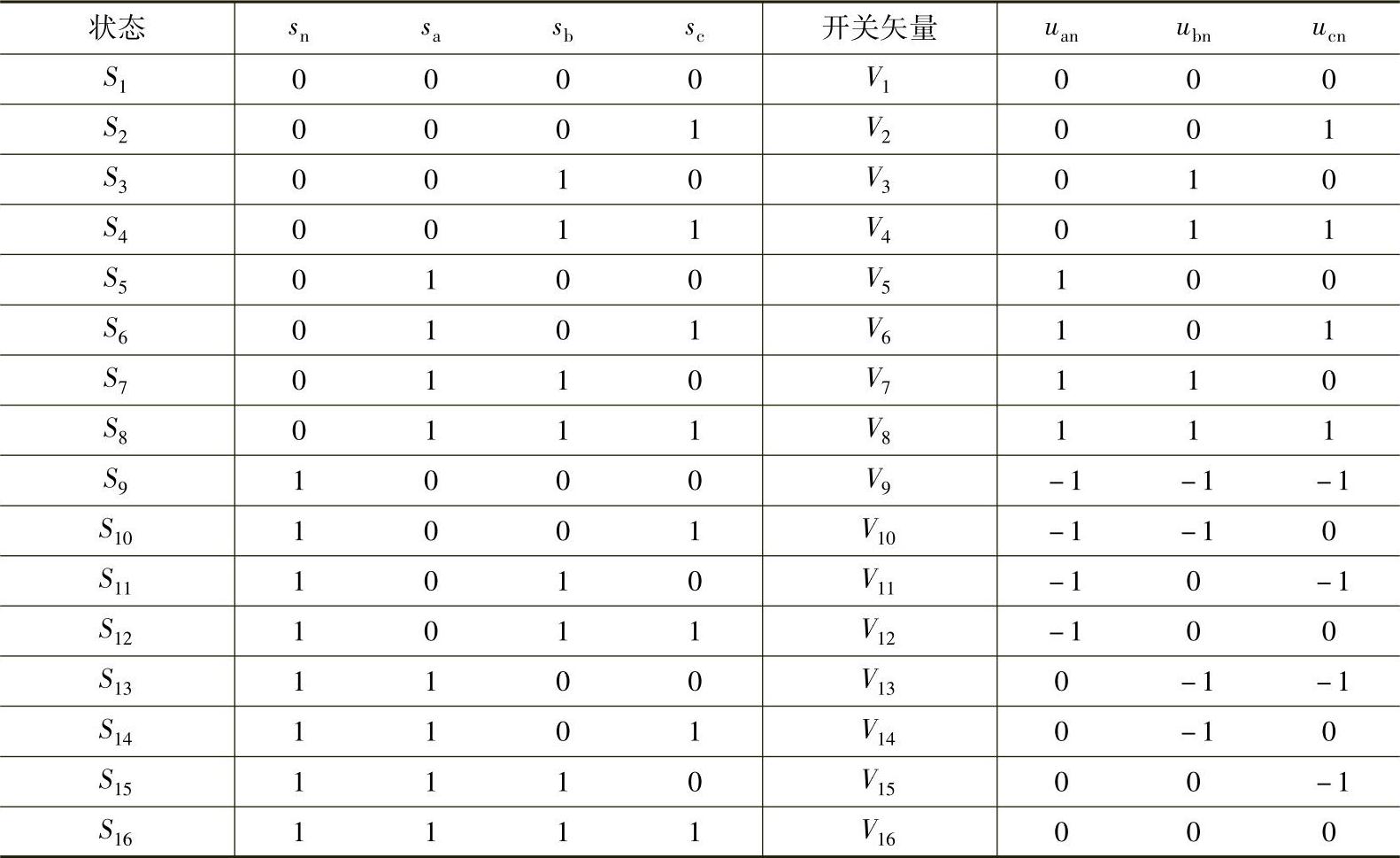
表5-5 三相四桥臂逆变器开关状态与输出电压

逆变器三相输出电压u_an、u_bn和u_cn可以用α-β-γ坐标系中的空间矢量来表示，只是此空间矢量定义在三维空间中定义：

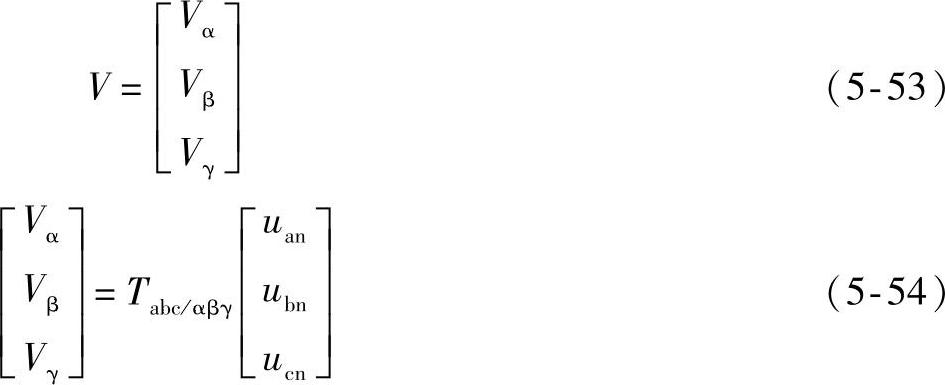
式中

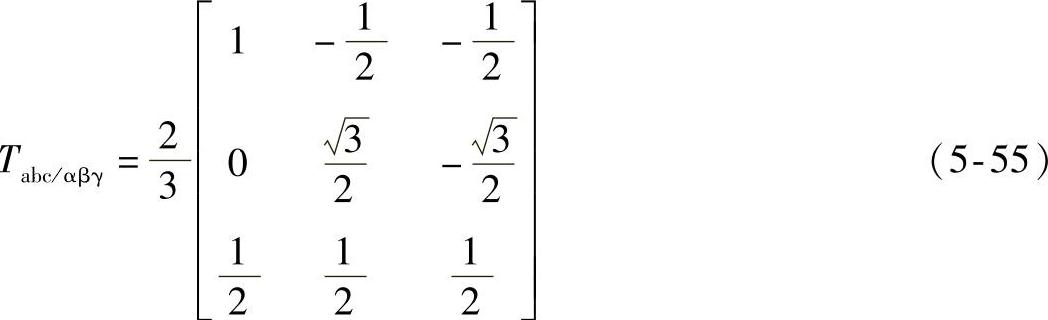
将所有16组开关矢量在αβγ空间坐标系中描绘出来，如图5-39所示。可以看出，这16个空间矢量都位于一个空间六棱柱内。3D SVM就是运用αβγ坐标系下的开关矢量来合成参考矢量V_ref，在原理上与二维空间矢量调制相类似。在abc坐标系下的参考电压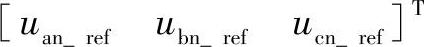经过式（5-54）的坐标变换，可以得到αβγ坐标系下的参考矢量。

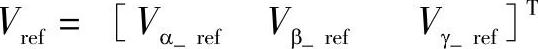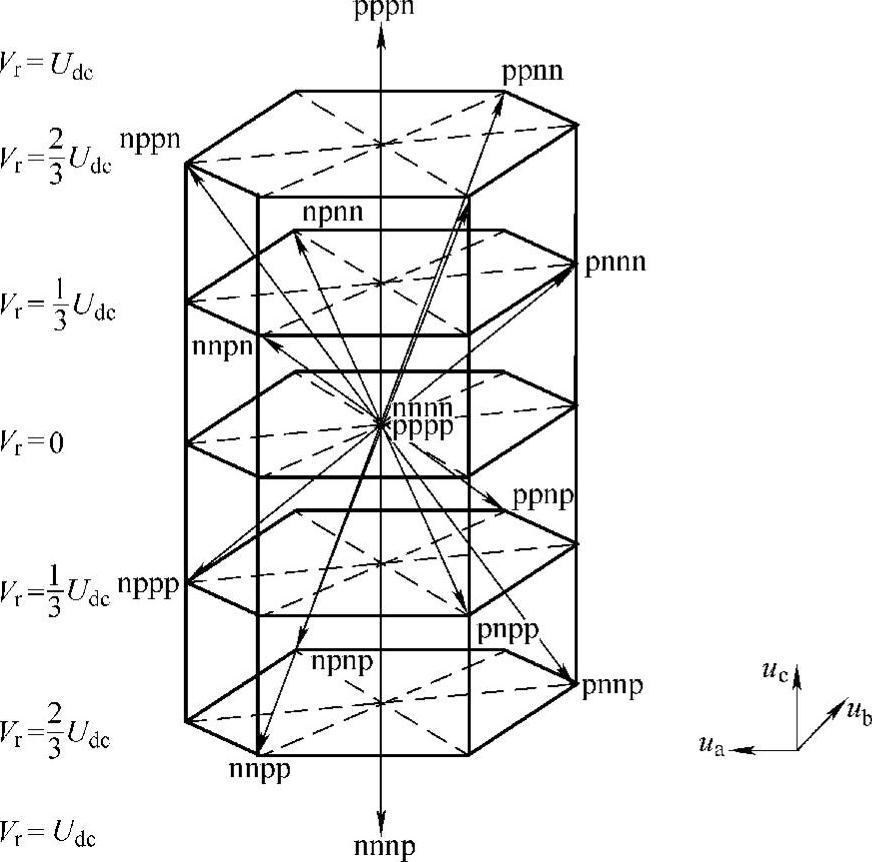
图5-39 三相四桥臂逆变器开关矢量图

由于三相四桥臂逆变器的参考矢量是在三维空间内运动，所以，它的控制较为复杂。参考矢量在3维空间坐标系下的合成主要有以下步骤：①选择合适的相邻开关矢量进行合成，首先确定参考矢量所在的三棱柱，其次再判断参考矢量位于哪一个四面体内；②计算出各自开关状态对应的占空比；③选取的开关矢量按照一定顺序进行组合，生成对应矢量调制的控制波形。

这种基于αβγ坐标系的3D SVM策略虽然可以很好地完成空间参考矢量的合成，但是存在以下几点不足：首先，这种方法需要进行坐标变换，增加了计算的复杂性；变换到αβγ坐标系下的开关矢量物理意义不清晰，很难直观地表示出参考矢量的位置，这个缺点在多电平逆变器应用中更加明显；基于αβγ坐标系的3D SVM需要判断参考矢量所在的三棱柱和四面体，涉及大量的三角计算，比较判断等。实际上，基于αβγ坐标系的计算更多的是基于对2D SVM继承而不是实用的考虑，与2D SVM不同，这种abc到αβγ的坐标变换反而使得问题的处理变得复杂。

2.基于abc坐标系的3DSVM

简化的三相四桥臂逆变器原理图如图5-40所示。由于三相四桥臂逆变器中增加了额外的桥臂，逆变器的输出相电压（u_an，u_bn，u_cn）可以独立控制，因此，三相输出电压必须在三维空间里表示。

三相输出电压的数学表达式如式（5-56）所示。

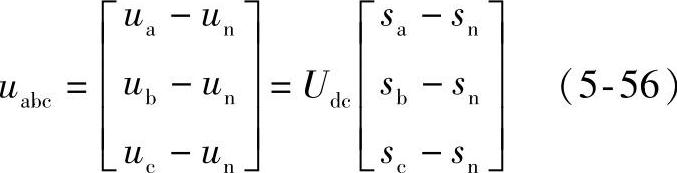
其中，s_i（i=n，a，b，c）为第i桥臂相应的开关函数。桥臂上管导通下管关断时的s_i=1，桥臂上管关断下管导通时的s_i=0。

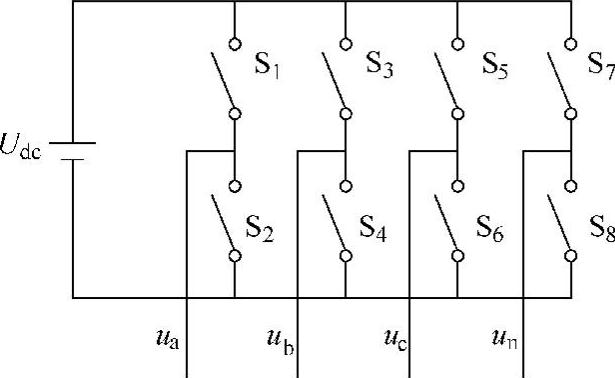
图5-40 简化的三相四桥臂逆变器电路拓扑

根据三相四桥臂逆变器的不同的开关组合，通过式（5-56）可以计算得到16种开关矢量，见表5-6。为了表达清晰起见，表5-6中所有的矢量都以母线电压U_dc进行归一化计算。此外，表5-6中的状态矢量S_i（i=1，…，16）和开关矢量V_i（i=1，…，16）都是列矢量。从表5-6中可以看出，如果将16个开关矢量绘制在三维abc坐标系中，所有的开关矢量都将位于两个边长为1的正立方体的顶点上：开关矢量V₁～V₈构成立方体位于全正的空间区域，V₉～V₁₆构成的立方体位于全负的空间区域，如图5-41所示。

表5-6 abc坐标系下的开关矢量表

从图5-41中可以看出，两个立方体的公共顶点恰好可以代表两个零电压矢量V₁和V₁₆。将各个正立方体中与开关矢量相关的顶点连接起来可以构成一个12面体。通过比较可以发现，这个12面体与基于αβγ坐标系的12面体围成的区域是完全等效的，然而，abc坐标系下的开关矢量更清晰直观，并且可以实现更简单的空间矢量调制算法。abc坐标系与αβγ坐标系在空间中的关系如图5-42所示。

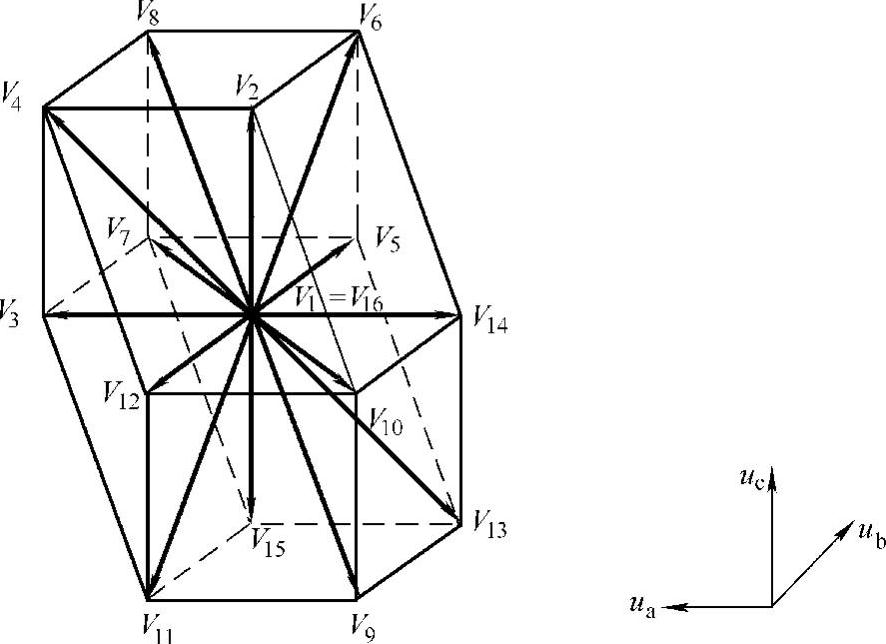
图5-41 abc坐标系下的开关矢量空间分布

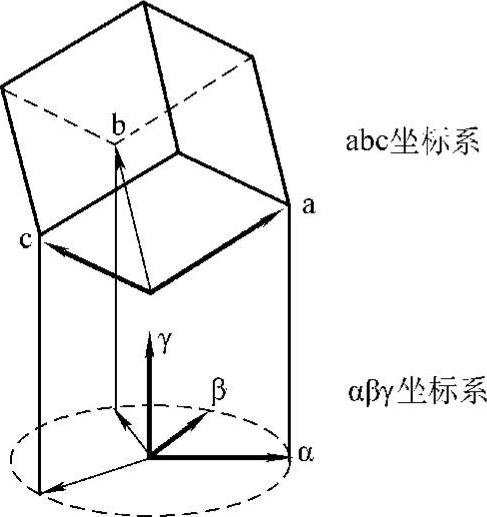
图5-42 abc坐标系与αβγ坐标系在空间中的关系

因为需要合成的空间矢量的轨迹必须位于图5-41所示的12面体内，因此有必要确定围成12面体的各个平面的表达式。由于采用了abc坐标系，这些平面的表达式非常简单。

六个平面平行于坐标轴，平面方程分别为u_a=±1，u_b=±1和u_c=±1。实际上这六个平面围成了一个边长为2的大立方体，并将12面体包括在内。这个大立方体具有实际的物理意义，它表示了三相四桥臂逆变器的输出相电压要小于或等于直流母线电压。

其余6个面与坐标平面夹45°角。平面方程分别为u_a-u_b=±1，u_b-u_c=±1和u_c-u_a=±1。这6个面也具有明确的物理意义，它们表示三相四桥臂逆变器的输出线电压也要小于或等于直流母线电压。

必须注意到所有的开关矢量也都与坐标面平行或相差45°夹角。并且，如果12面体构成的控制区域被平面u_i=0（i=a，b，c）和平面u_i-u_j=0（i，j=a，b，c；i≠j）分割的话，可以很容易地验证：分割后得到24个四面体形状的小区域，并且每个四面体都包含相同数目的开关矢量，即三个非零矢量和两个零矢量。其中，三个非零矢量构成了四面体的三条棱边，两个非零矢量位于四面体的一个顶点上。

一般说来，空间矢量调制技术用于产生一个与参考电压矢量等效的平均电压矢量。为了达到这个目标，逆变器的每种开关状态都要用对应的开关矢量表示。通过在确定的开关周期内选择恰当的开关矢量，来产生一个与参考电压矢量等效的电压矢量。

如前所述，对于三相三线系统，由于输出电压只有两个完全独立，因此通常将abc三相电压转换到αβ坐标系下进行处理。此时，8个开关矢量中心对称分布在一个六边形内。通过判断参考矢量所在的60°扇形区域来选择合适的开关矢量进行合成。基于abc坐标系的3D SVM与2D SVM相似，只是需要判断的区域不再是60°扇形区域，而是包含5个开关矢量（3个非零矢量，两个零矢量）的四面体。一旦判断出了参考矢量所在的四面体，依照伏秒平衡原则，就可以确定每个开关矢量作用时间（或占空比），从而得到平均意义上的参考矢量。3D SVM通过在abc坐标系下的处理，极大地简化了四面体的选择和计算各个开关矢量占空比的时间。另外一个重要问题是开关顺序问题，也就是选择开关矢量的作用顺序。采用不同的开关矢量排列顺序，开关损耗和输出电压THD也各不相同。

1）四面体的选择

前面已经提到，控制区域可以被分割为24个四面体，每个四面体中都包含3个非零矢量和2个零矢量。图5-43展示了全部24个四面体在控制区域中的位置以及对应的开关矢量。从图5-43中可以看出，两个正立方体所占的区域被分成了12个四面体，剩余的两个正立方体之间的区域也被分成了12个四面体。所有的这些四面体大小相等，是控制区域的对称划分。因此，通过应用分割平面的方程，可以决定具体哪一个四面体包含了参考矢量。一种方便的算法如式（5-57）所示。

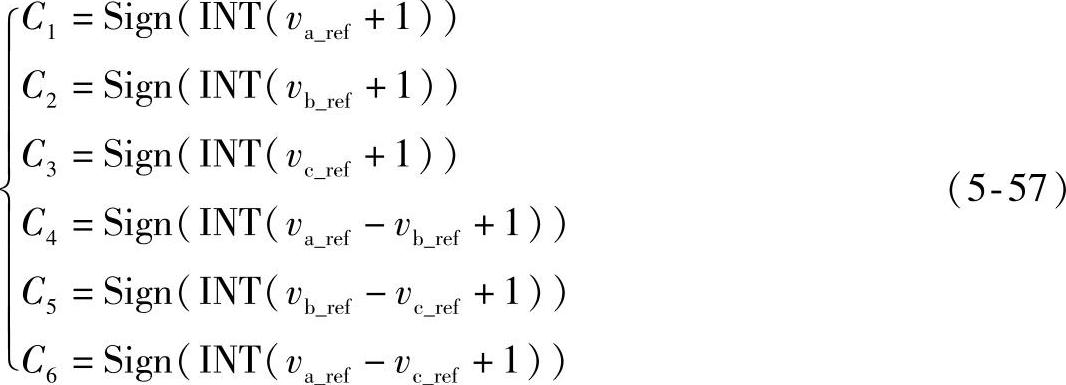
式中，C_i（i=1～6）代表了参考矢量相对于分割平面的位置。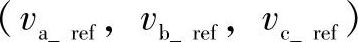为以母线电压U_dc归一化的参考电压矢量。

(www.daowen.com)

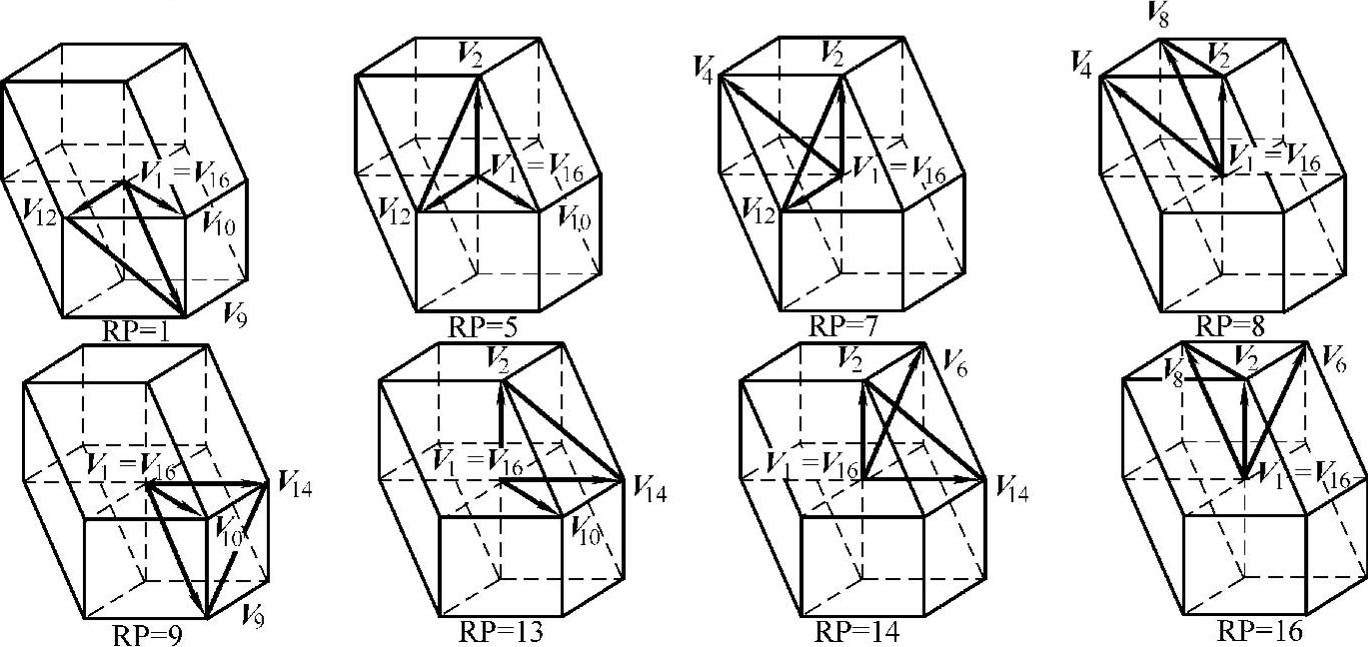
图5-43 用于辅助确定参考矢量位置的24个四面体

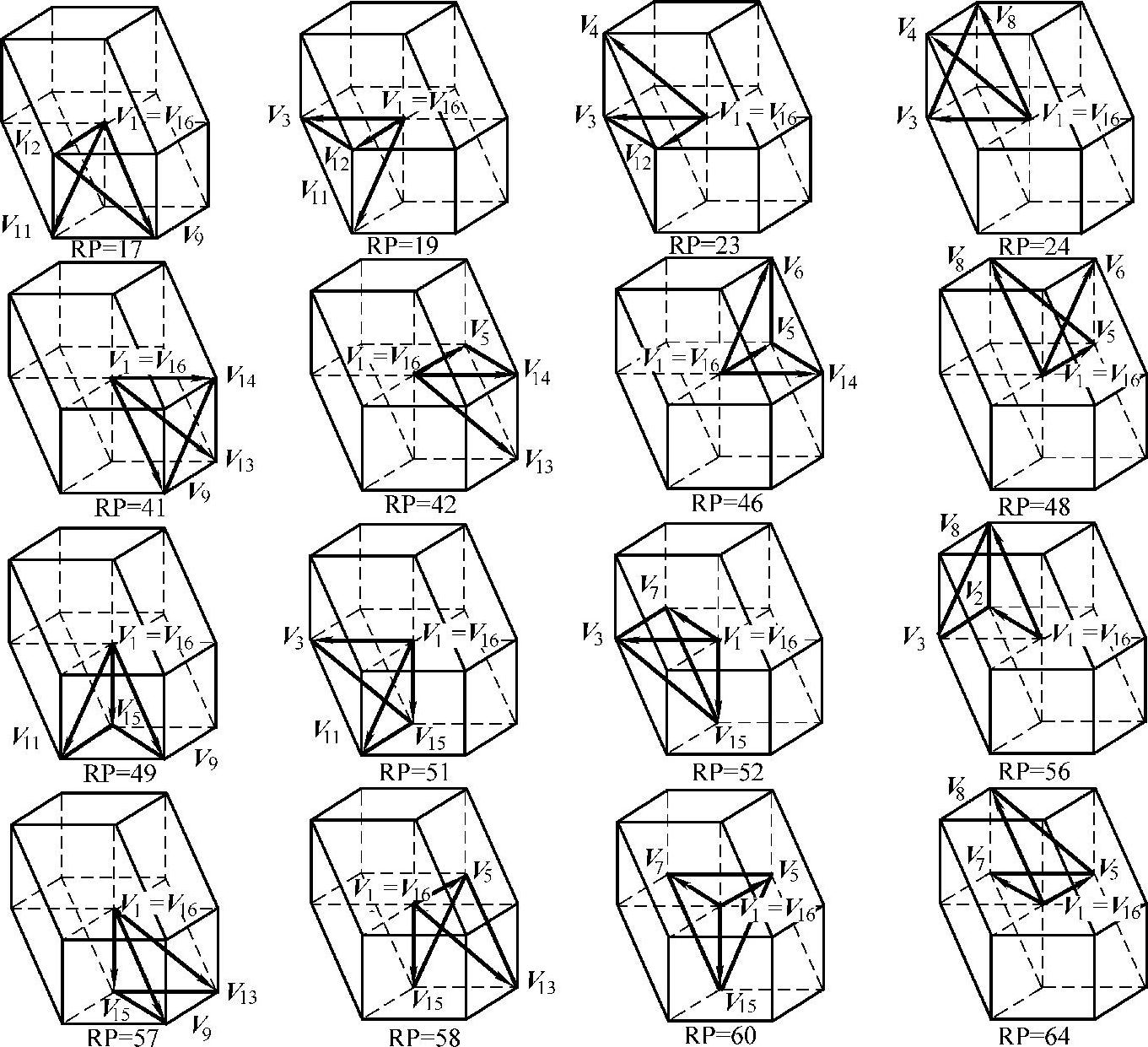
图5-43 用于辅助确定参考矢量位置的24个四面体（续）

INT（x）为取整函数。Sign（x）为取符号函数：如果x>0，Sign（x）=1；如果x=0，Sign（x）=0；如果x<0，Sign（x）=-1。注意到参考电压矢量总是落在控制区域内，C_i的取值只能是0或1。可以看到，由式（5-57）描述的计算很容易由微处理器完成。

2）开关矢量占空比的计算

定义一个指向参考电压所在四面体的区域指针变量RP：

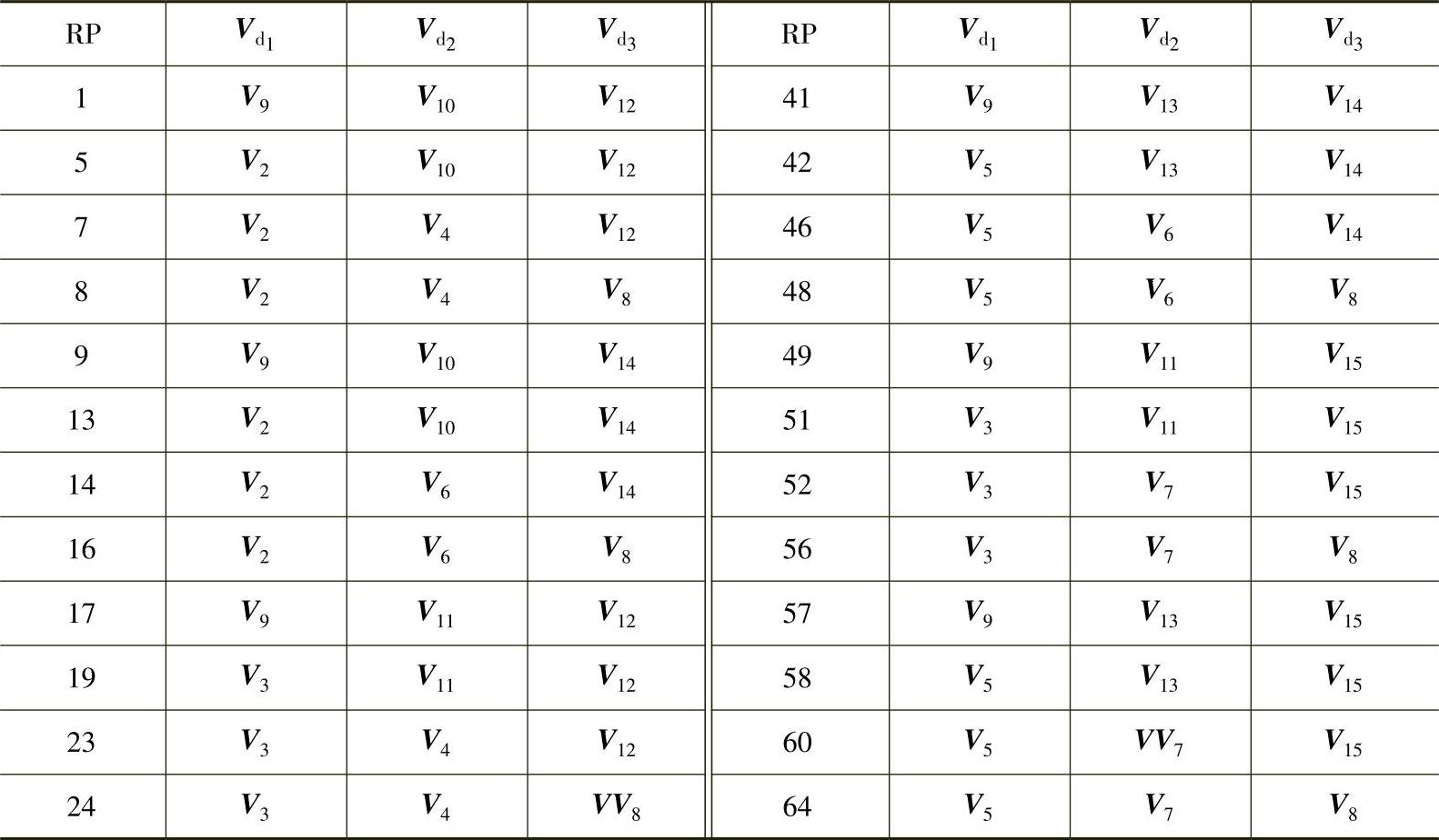
理论上RP的取值范围为1～64，实际上由于C_i的取值并不完全独立，RP只能取到其中24个可能的数值。正好对应24个四面体。用V_d1，V_d2和V_d3代表四面体中的3个非零开关矢量，V_d0代表四面体中的两个零矢量。计算得到的RP与对应的四面体包含的非零矢量的关系见表5-7。可以看到，式（5-58）的计算过程很简单，仅仅需要一些移位和加法运算，且式（5-57）也只需要简单的条件判断语句即可完成。在浮点DSP TMS320C31-50MHz上运行程序实现上述计算过程仅需0.8μs，同样的计算过程如果在abg坐标系下进行，至少需要4μs。

表5-7 24个四面体的区域指针RP与对应非零开关矢量的关系

3个非零矢量确定后，需要确定应用哪种开关排列顺序，也就是决定开关矢量的作用顺序。根据不同的零矢量加入方式和开关矢量排列顺序是否对称于开关周期，可以组合出许多种开关样式。图5-44给出了其中一种开关排列顺序。

图5-44中，d₁、d₂和d₃分别为三个非零矢量V_d1，V_d2和V_d3的作用时间对开关周期的占空比，d₀为零矢量V_d0的作用时间的占空比。这是一种开关矢量对称排列的方案，只添加了一种零矢量。这种方式的特点是在一个工频周期内，对于A、B和C桥臂而言，每个开关管都有1/3的时间不动作，开关损耗小。

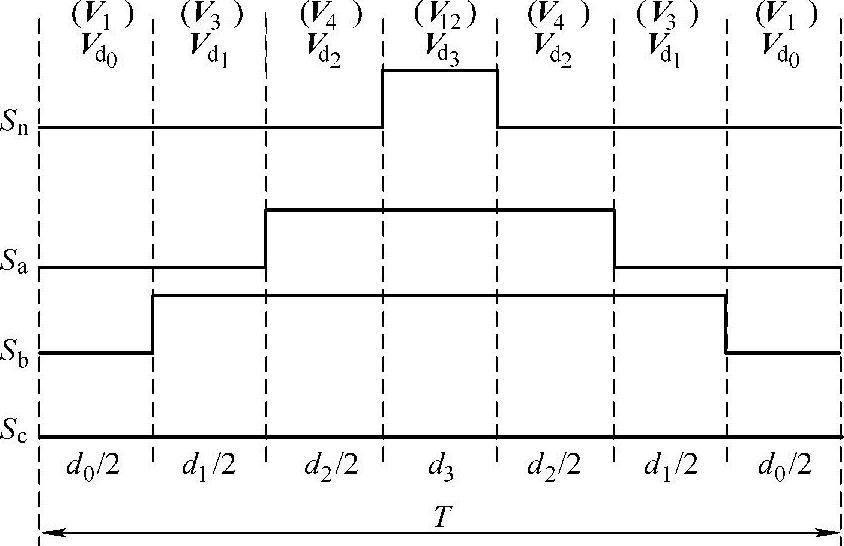
图5-44 开关矢量的作用顺序（RP=23）

在图5-44中，给出了在RP=23的四面体区域中，3个非零矢量实现的开关动作顺序及作用时间d₁、d₂、d₃和d₀。在不同的四面体中，也就是对应不同的RP，需要应用不同的非零矢量，开关动作的顺序和作用时间各不相同。为了得到各个桥臂开关的占空比，首先要计算出不同的RP所对应的3个非零矢量的作用时间及零矢量作用时间。依照伏秒平衡原则有，参考电压矢量V_ref可以表示为

零矢量作用时间：

d₀=1-d₁-d₂-d₃（5-60）

式（5-59）和式（5-60）可以表示为d₁+d₂+d₃+d₀=1，则有：

V_ref=M_dd（5-61）

式中，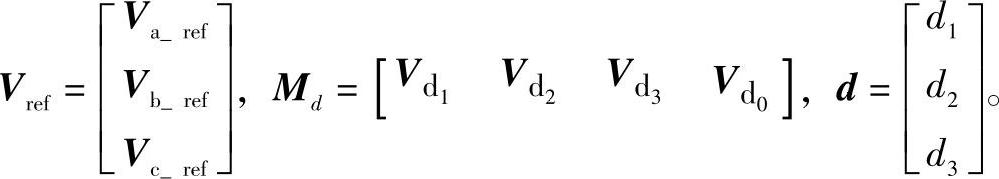

由式（5-57）可以计算出非零矢量的作用时间：

表5-8列出了与24个四面体对应的转换矩阵M_d和M_d^-1。从表中可以看出，矩阵M_d的元素只是0、1或-1，表达式非常简洁。同样M_d^-1的元素也全部是0、1或-1。因此，式（5-62）实际上只是一些加减法运算，非常简单。

非零矢量的占空比d₁、d₂、d₃确定后，零矢量的占空比d₀由式（5-63）计算：

d₀=1-d₁-d₂-d₃（5-63）

3）开关管导通时间占空比的计算

因为逆变器的输出电压最终是由开关管的导通关断实现的，求出开关矢量的占空比后，还需要确定每个桥臂开关管的占空比。将A、B、C和N 4个桥臂的上管导通时间对开关周期的占空比分别记为d_a、d_b、d_c和d_n。例如，以图5-43所示的RP=23时的开关顺序确定开关的占空比，可以很容易地看出：

式（5-64）可以写成矩阵形式：

式中，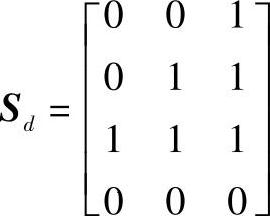

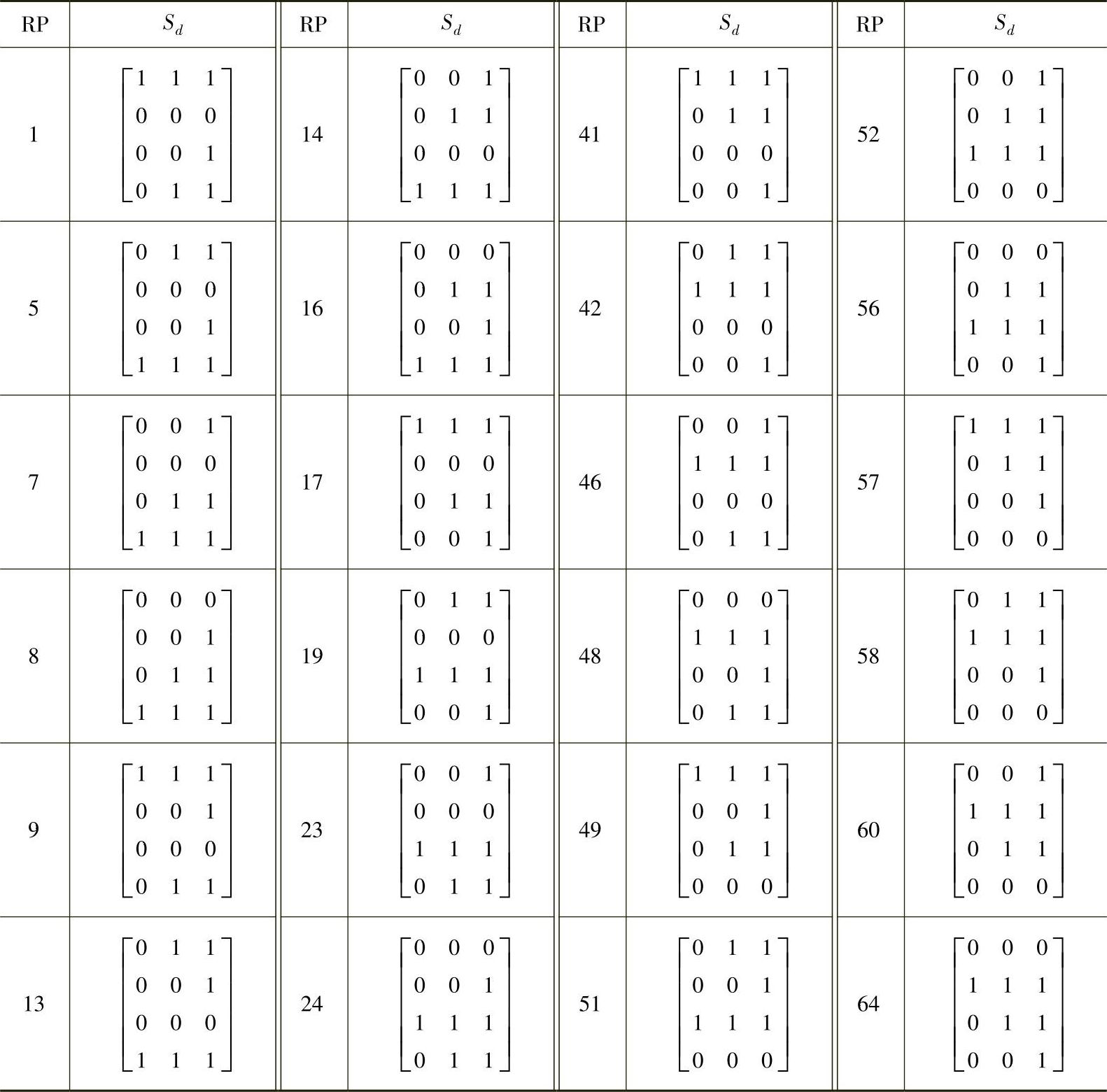
实际上，S_d是由非零矢量对应的开关函数状态构成的，对于RP=23，S_d=[^S₃S4 S12]。不同的RP，变换阵S_d也不同，也就是说，一共有24个不同的变换阵S_d，见表5-9。得到了每个桥臂开关管的占空比d_a、d_b、d_c和d_n后，就可以通过微处理器发出对应的PWM波形信号。

表5-8 用于计算非零矢量作用时间的转换矩阵M_d和M_d^-1

表5-9 开关管占空比计算矩阵S_d