1.SVM调制波的显化

SVM的调制过程是在矢量空间实现的，而SPWM是在A-B-C坐标系下分相实现的。SPWM的相电压调制波是正弦波，而SVM的相电压调制波是隐含的。为了揭示SVM与SPWM的内在联系，需要求出SVM在A-B-C坐标系上的等效调制波；也就是将SVM的隐含调制波显化。为此，首先简单介绍一下对称规则采样法SPWM。

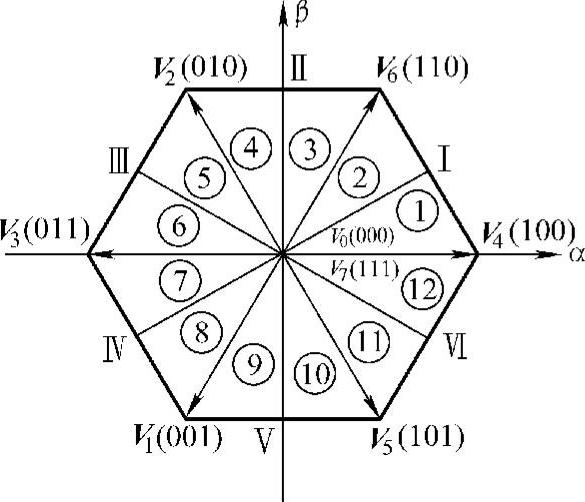
图5-28 调制方法四对应的矢量分区图

对称规则采样法SPWM的原理图如图5-29所示。正弦调制波信号为U（t）=Msinωt。由图5-29，可以解出脉宽t_pw的表达式为

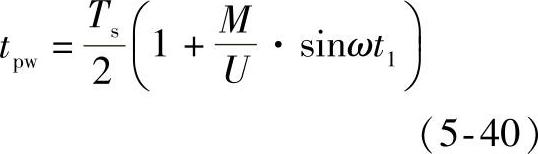
式（5-40）就是规则采样法SPWM的基本公式。

从图5-29和式（5-40）可以看出在规则采样法下，对应于给定相电压调制波U[φ（k）]=M·sin[φ（k）]，在线性调制区的驱动信号的脉宽调制函数：

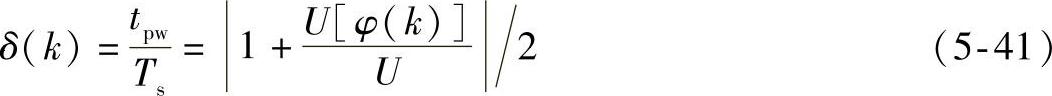
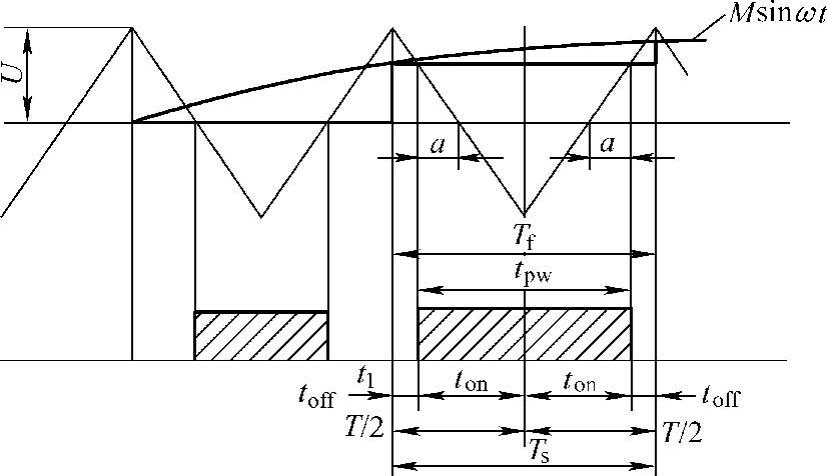
图5-29 对称规则采样法

SVM方法实质上也属于规则采样法，只不过隐含了相电压调制波。对于SVM方法，如果能够得到类似于式（5-41）的脉宽调制函数，就可以逆向推出其等效的相电压调制波。

对于图5-26所示的常规SVM波形，只讨论A相，可以得到第Ⅰ扇区的脉宽调制函数为

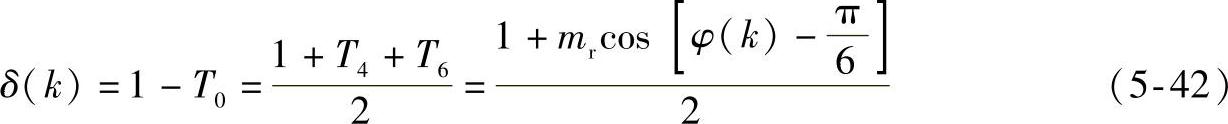
因此，可知第Ⅰ扇区a相相电压调制波的表达式就是：

同理，可推出其他各扇区的相电压调制波形；最终得到总的a相相电压调制波函数如下：

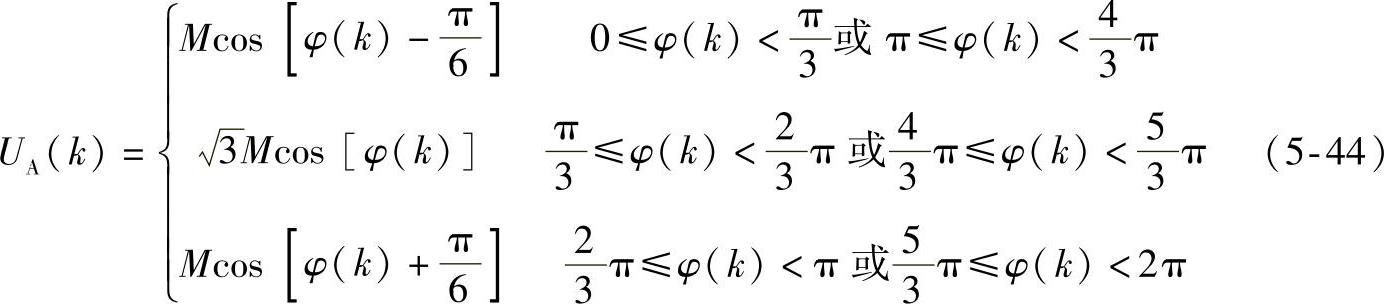(www.daowen.com)

b相、c相的相电压调制波函数同样也能获得，图5-30所示就是常规SVM的三相等效相电压调制波。根据三相等效相电压调制波，可以得到等效线电压的波形；等效线电压为一个标准正弦波，如图5-30所示。

很明显，SVM的相电压调制波不是标准正弦波，而是在正弦波中注入一些高次谐波分量。图5-31给出的是SVM的等效相电压调制波、对应的标准正弦波以及二者之间的差值。因此在图5-31中的标准正弦波U_AN中注入高次谐波成分U_N，就可以得到合成波形U_AO。以U_AO代替标准正弦波，进行规则采样调制，就可以得到与电压空间矢量调制效果完全相同的PWM波形。

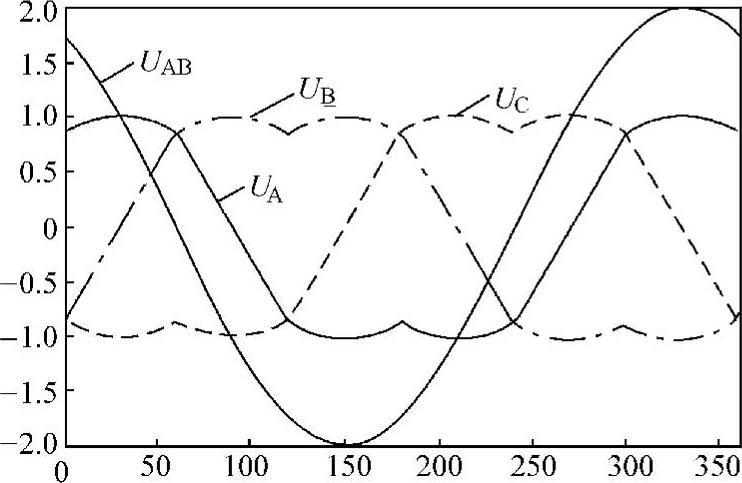
图5-30 常规SVM的等效相电压调制波形（幅度调制比为1）

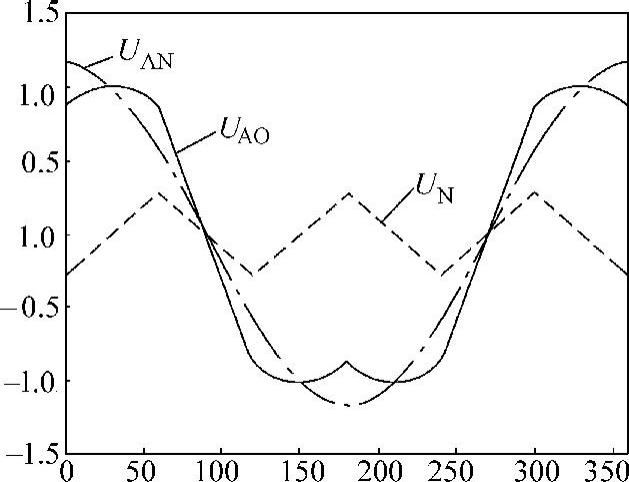
图5-31 常规SVM的等效相电压调制波、对应的标准正弦波以及二者之间的差值

上面的分析实际上揭示了SVM技术与HIPWM之间的内在联系。对比图5-31和图5-17，可以发现二者完全一致，也就是说SVM与HIPWM等效。

MSL-SVM的相电压调制波也可以按照以上的办法得到相电压调制波的显式函数。根据调制波的数学表达式，可以绘出SVM的相电压调制波波形。方法一～方法四的调制波波形如图5-32所示（幅度调制比为1）。其中细实线为a相，虚线为b相，点画线为c相，粗实线为线电压。从图5-32可知，尽管4种方法的调制算法互不相同，其相电压波形也各不相同，但线电压波形却完全一致，是同相同幅的标准正弦波。与HIPWM对比可知，方法一对应于由式（5-21）合成的HIPWM，方法二对应于由式（5-22）合成的HIPWM，方法四对应于由式（5-24）合成的HIPWM。

2.MSL-SVM技术的谐波分析

从各种方法的相电压调制波波形和调制原理来看，可以定性地得到以下两点结论：

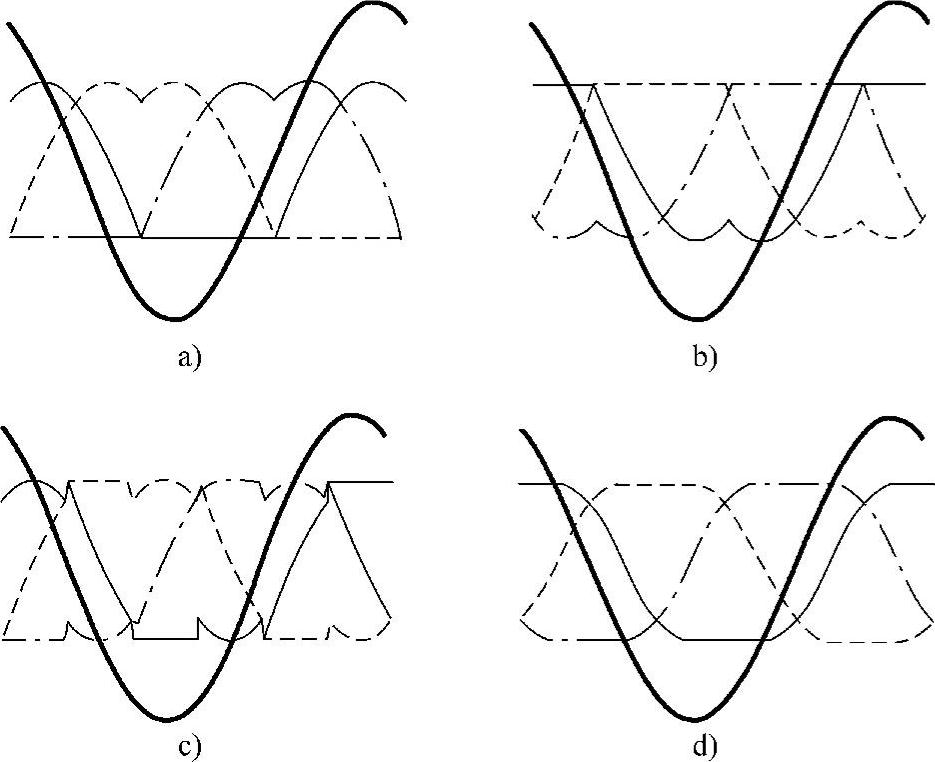
图5-32 4种MSL-SVM的调制波形

a）方法一 b）方法二 c）方法三 d）方法四

（1）从形状上看，方法一和方法二的相电压调制波波形完全是相反的。将方法二的相电压调制波形垂直翻转180°，得到的波形在形状上与方法一的相电压调制波完全相同；当然相位上有差。从傅立叶变换的性质可知，波形的翻转和相位移动只影响各次谐波的相位，不影响它们的幅值。在相同的调制比下，在输出电压的谐波分布和谐波幅值上，采用方法一和方法二的效果完全一致。

（2）调制波波形上看，交替零矢量调制方式的调制波具有正负半周反对称性质，属于对称调制；而单一零矢量调制方式的调制波没有正负半周反对称性质，属于非对称调制。对称调制的谐波特性显然比非对称调制好，也就是说交替零矢量调制方式的谐波特性比单一零矢量调制方式好。方法四的调制波形在四种方法中对称性最好，因此其谐波特性也是最好的。

为了验证以上两点结论，分别采用上述4种方法调制，进行了仿真研究。图5-33所示的是分别采用4种方法调制，输出线电压的频谱图（幅度调制比为0.9，频率调制比为27）。比较四种调制方法，从频谱分布上看，方法四最好；而方法一和方法二的频谱完全相同。这表明前面得到的结论是正确的。