1.电压空间矢量的概念

如图5-20所示，A、B、C分别表示在空间静止不动的电动机定子三相绕组的轴线，在空间互差120°，三相定子相电压u_a、u_b、u_c分别加在三相绕组上，可以定义3个电压空间矢量u_A0、u_B0、u_C0，它们的方向始终在各相的轴线上，而大小则随时间按正弦规律做变化，时间相位互差120°。

假设M为相电压幅值，f为电源频率，则有：

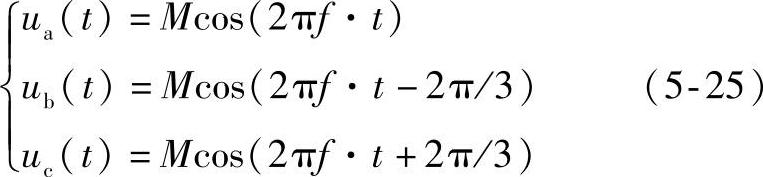
假设单位方向矢量，则三相电压空间矢量

相加的合成空间矢量V（t）就可以表示为

可见V（t）是一个旋转的空间矢量，它的幅值不变；当频率不变时，以电源角频率2pf为电气角速度做恒速同步旋转，哪一相电压为最大值时，合成电压矢量就落在该相的轴线上。

图5-20 电压空间矢量

对于如图5-11所示的常规三相电压型逆变器，引入开关函数S_A、S_B和S_C，分别代表3个桥臂的开关状态。s_X（X=a，b，c）是一个二值变量，上桥臂器件导通时s_X=1，下桥臂器件导通时s_X=0。（s_a，s_b，s_c）组合在一起，有V₀～V₇共8种基本工作状态，即：000、001、010、011、100、101、110、111。其中V₁～V₆这6个工作状态是有效的，称作非零矢量；V₀、V₇这两个工作状态称作零矢量。图5-21所示是复平面上三相电压型桥式变流器的基本矢量分布。

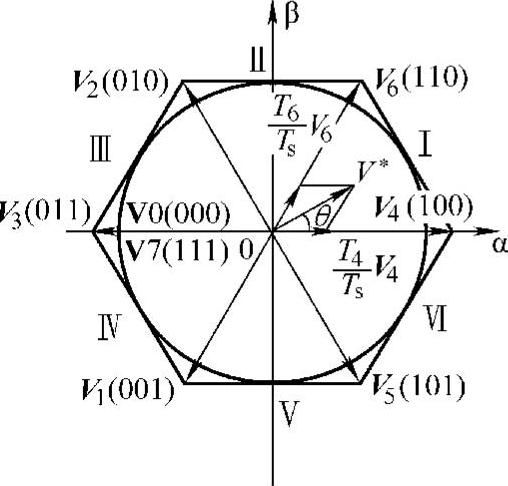
图5-21 在复平面下三相电压型桥式变流器基本矢量图

2.磁链跟踪PWM的基本思想

在三相对称电压作用下，对于图5-22中所示的三相电动机，如果忽略定子绕组的电阻不计，则电动机各相磁链值可由式（5-27）进行积分得到：

将式（5-27）所示三相轴系的磁链进行坐标变换，由图5-22中所示的三相A-B-C轴系变换到图中所示的d-q轴系，其变换式为

将式（5-28）代入式（5-27）进行变换，得到d-q轴系的磁链矢量

式中 Ψ_m——磁链圆的半径。

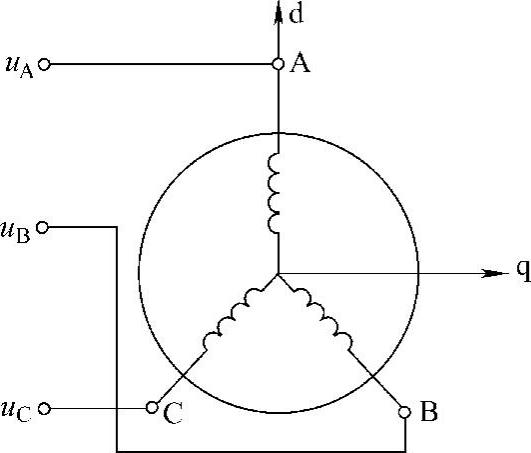
图5-22 三相对称正弦波电压驱动三相对称电动机

其中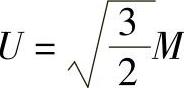，为电动机线电压有效值（V）；θ=ωt=2πft为电角度。由式（5-29）、式（5-30）可知，当电压频率比U/f为常数时，磁链圆半径Ψ_m为常数。这样，随着θ（t）的变化，磁链矢量Ψ_dq（θ）就形成一个以Ψ_m为半径的圆形轨迹，即得到一个理想磁链圆。如图5-23所示。在磁链追踪型PWM法中，就是以此理想磁链圆为基准圆。磁链矢量与前述的电压空间矢量一一对应，其大小与对应电压矢量持续的时间以及直流电压U_d的大小有关。若假定8种电压矢量对应的开关模式持续时间T相等，将不同开关模式下作用于电动机三相绕组上的电压对T进行积分，则可得三相磁链在T期间的增量[ΔΨ_AΔΨ_BΔΨ_C]^T。将此三相磁链矢量增量（以下简称为磁链矢量）用式（5-28）中的变换阵，由A-B-C三个轴系变换到d-q轴系，可得图5-24中所示d-q轴系的8种磁链矢量，其大小可表示为

其中，

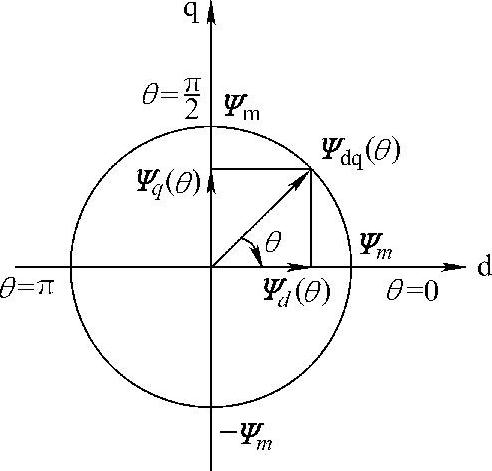
图5-23 d-q轴系中磁链矢量及理想磁链圆

图5-24 逆变器驱动时电动机的磁链矢量

以上是假定6种非零矢量开关模式下，U_dc、T都相等。而实际上，各种开关模式下，中间直流电压U_dc未必是一个定值，积分时间T也不要求恒定。当U_dc或者T不同时，图5-24中各磁链矢量的大小自然也不同。

将图5-23所示的理想磁链圆作为基准圆，适当地使用图5-24中8种磁链矢量追踪基准磁链圆。使用不同的磁链矢量，意味着使用不同的开关模式。开关模式的切换，则形成逆变器输出电压PWM波。不难理解，如果这8种磁链矢量能够很好地追踪基准磁链圆，则逆变器输出三相电压也一定是三相对称的正弦PWM波。这就是磁链追踪型PWM法的基本思想。

3.SVM的电压采样解释及SVM基本算法(www.daowen.com)

从式（5-26）可以明显看出电压矢量V（t）在复平面上随时间变化的轨迹为圆。如果对三相定子相电压u_a、u_b、u_c进行采样，其采样频率f_S（T_S=1/f_S），则离散矢量V可表示为

式中 φ（k）——在第k个采样周期所对应的位置角。

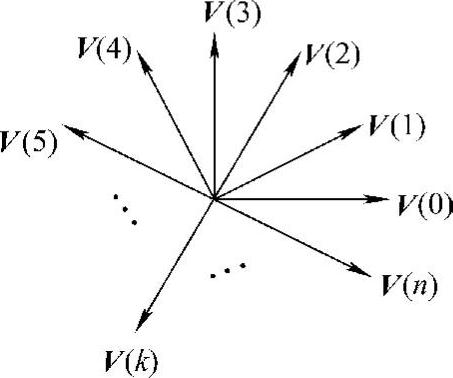
图5-25 离散的电压矢量图

当k从0～n（n=f_S/f）变化时，V（k）在复平面上就形成了一系列的离散矢量，如图5-25所示。

前面已经谈到，在常规三相电压型逆变器中，只能得到8个基本矢量。在一个开关周期T_S内，图5-21中的参考矢量V*作用效果可以由与其相邻的两个非零矢量和零矢量来合成（线性表示）。矢量合成方程如下：

式中，，x=4，6，z；t_x为对应矢量的作用时间。

事实上，图5-25中的任意矢量都可以由这8个基本矢量合成。式（5-33）中零矢量V_z可以是V₀、V₇的组合，也可以单独使用其中一个，零矢量的作用时刻也可以选择，因此零矢量的分配关系与作用时刻的不同安排可以得到不同的调制方式。

从图5-21可以看出，6个非零矢量将整个平面分成6个扇区。以第Ⅰ扇区为例，依照平行四边形法则，有

T₄V₄+T₆V₆=T_SV*（5-34）

由（5-34）解得

其中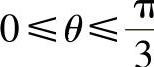π；T₄、T₆不足时，插入零矢量补足，一般地，有：

式中，T₀₀、T07分别代表零矢量V₀、V₇的作用时间，0≤k≤1。其他扇区的调制算法完全相同。定义幅度调制比m_r为

从式（5-35）、式（5-36）可见，电压空间矢量调制的线性调制约束条件是：

T₄+T₆≤T_S（5-38）将式（5-35）、式（5-36）代入式（5-38），有：

式（5-38）、式（5-39）对于任何θ都应成立，而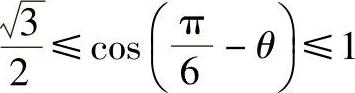，因而幅度调制比m_r的最大值为1，也就是说逆变器输出相电压的极限峰值是。反映在矢量图上，最大电压空间矢量的轨迹就是图5-21所示的正六边形的内切圆。传统的SPWM最大相电压峰值是U_dc/2，因而SVM的直流电压利用率比SPWM提高了15%。以上推导过程与矢量发送顺序和k值无关，因此，高直流电压利用率是SVM的本身特性。无论以何种方式产生SVM波形，只要满足式（5-35）、式（5-36），其电压利用率都是一样的。进一步计算可知，m_r取1，也就是SVM输出最大时，线电压峰值等于U_dc，已经达到直流母线电压；再继续增加就超出线性调制了，所以SVM的直流电压利用率是最高的。

式（5-36）中k的不同取值对应着不同的调制模式，在谐伯德性和开关损耗上也有不同的特点。一般将SVM的调制模式分为两种：常规SVM和最小开关损耗SVM。常规的SVM策略在一个采样周期内有6次开关动作，与SPWM的开关频率相同。以第一扇区为例，其在一个采样周期内的开关触发波形如图5-26所示。其中T₄、T₆为矢量V₄、V₆的作用时间，T₀、T₇为零矢量V₀、V₇的作用时间，T_S为采样周期。

常规的SVM在一个采样周期内有6次开关动作，从减小开关损耗的角度出发，又出现了最小开关损耗空间矢量调制（Minimum Switch Loss SVM，MSL_- SVM）。

4.最小开关损耗SVM

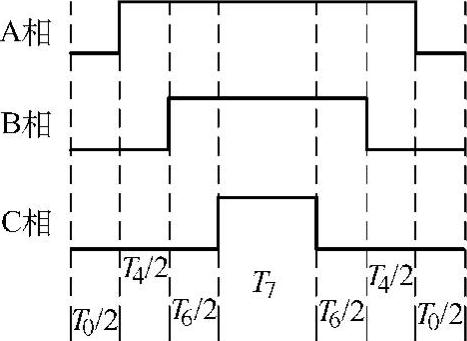
图5-26 常规SVM在一个采样周期内的开关波形

MSL-SVM通过适当选择零矢量使用方式，使得在一个采样周期内的开关动作减少为4次，从而将开关频率减小了33%，开关损耗大大降低；这对于提高装置功率等级、降低系统电磁干扰（EMI）有非常积极的意义。

MSL-SVM在一个采样周期内只采用一种零矢量，具体的有两种方式。以第Ⅰ扇区为例，一个采样周期内的开关触发波形如图5-27所示。

图5-27 MSL-SVM一个采样周期内的开关触发波形

实现MSL-SVM有两种方式。一种是在矢量图的所有区域中都使用同一个零矢量，这种方式称为单一零矢量调制方式。单一零矢量调制方式显然可分为两种方法：使用零矢量V₀的方法，本文称为方法一；以及使用零矢量V₇的方法，本文称为方法二。单一零矢量调制在降低开关损耗的同时，也增加了谐波成分。为了克服这一问题，可以采用交替零矢量调制方式。交替零矢量调制方式是根据参考矢量所在的不同扇区，使用不同的零矢量。比如当参考矢量位于Ⅰ、Ⅲ、V扇区时，零矢量V₀；当参考矢量位于Ⅱ、Ⅳ、Ⅵ扇区时，零矢量取V₇；本文将这种调制方法称为方法三。另外，还有一种交替零矢量调制方法，即将矢量平面平均分为12个区域，如图5-28中区域①～⑫所示。其中，区域①、④、⑤、⑧、⑨、⑫零矢量采用V₇，区域②、③、⑥、⑦、⑩、⑫⑪零矢量采用V₀；本文将这种调制方法称为方法四。交替零矢量调制方法除了以上几种，还有很多，这里就不一一列举了。