对于如图5-3所示的电压型单相全桥逆变器而言，有3种基本的SPWM技术：双极性SPWM、单极性SPWM和倍频式SPWM。下面分别介绍。

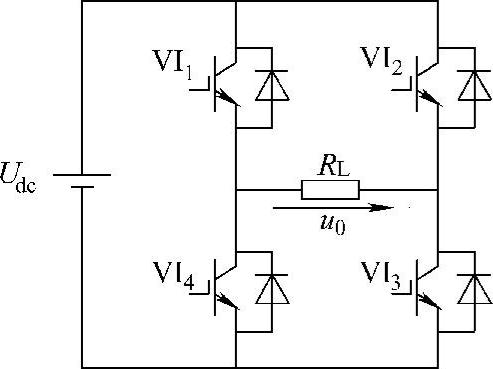
图5-3 电压型单相全桥逆变电路

1.双极性SPWM技术

1）双极性SPWM的基本原理

双极性SPWM技术的基本原理图如图5-4所示。载波信号u_c的重复角频率为ω_c，幅值为U_cm，一般可供选择的波形有锯齿波和对称三角波等，由于后者就有更高的控制灵敏度，故更受青睐，图5-4a中采用对称三角载波u_c，按图中所标时间坐标原点，调制信号可表示为

u_m=U_msinωt（5-1）

式中 ω——u_m角频率（ω=2πf）；

U_m——u_m的幅值。

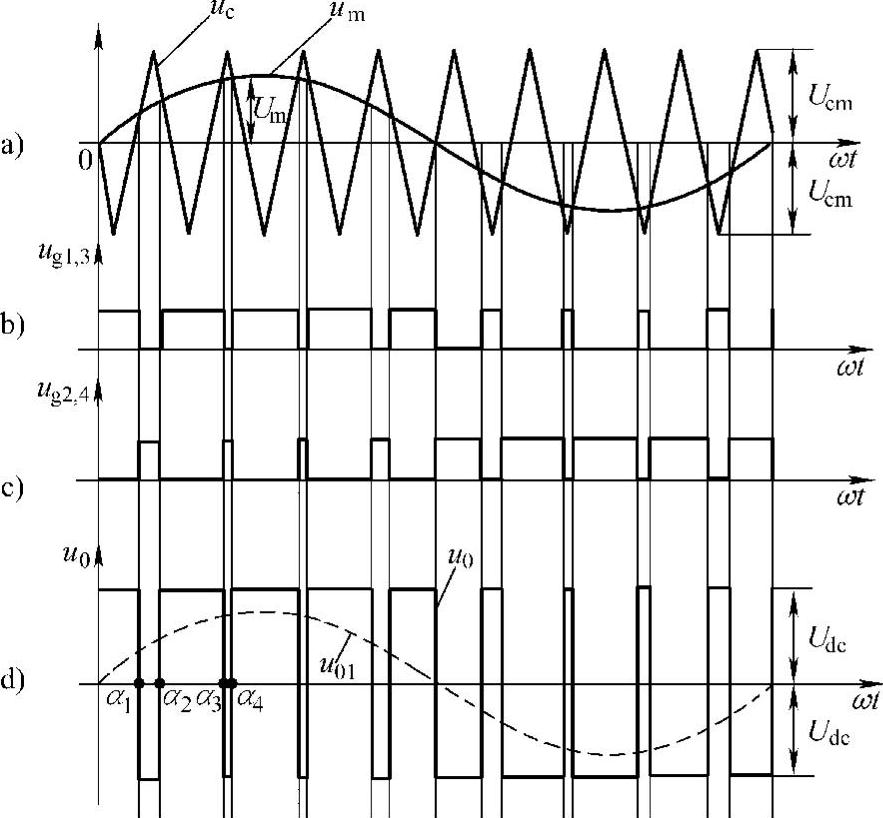
图5-4 双极性SPWM单相逆变电路的电量波形

调制比m被定义为

通常u_c幅值U_cm为恒值，于是m值随U_m线性变化。

频率比K定义为

采用u_c和u_m相比较的方法生成PWM信号，当u_m>u_c时，产生VI₁和VI₃的控制信号u_g1，3；当u_m<u_c时，产生VI₂和VI₄的控制信号u_g2，4。逆变桥中VI₁～VI₄将以载波频率f_c轮番导通。

当VI₁，VI₃导通时，输出电压u₀=U_dc；相反，当VI₂，VI₄导通时，u₀=-U_dc。图5-4中虚线u₀₁表示u₀中的基波分量，其幅值为u_01m。根据式（5-2）可得到：

2）双极性SPWM逆变器输出电压谐波分析

对双极性SPWM输出电压波形进行傅立叶分析，可以得到其谐伯德性图。图5-5所示是m=0.8，K=15时双极性SPWM的频谱。由于频率比K选为奇数，u₀波形具有奇函数对称和半波对称性质，故只含有奇次谐波。

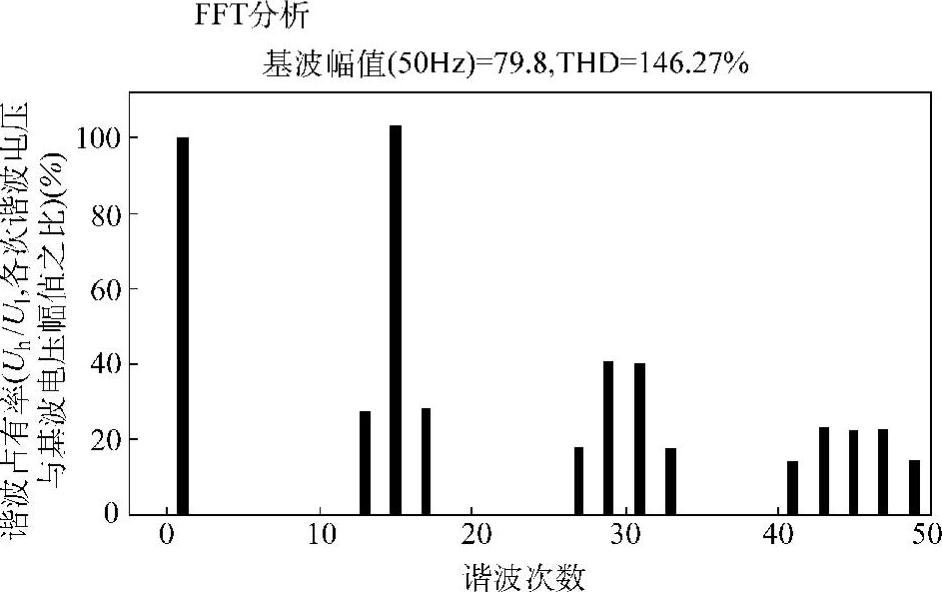
图5-5 双极性SPWM逆变器m=0.8，K=15时，输出电压频谱

由图5-5可见，整个频谱包含以下3种谐波：①基波：频率与调制波频率相同；②载波谐波：即载波频率整数倍次的谐波成分；③边带谐波：以各次载波谐波为中心，形成各个幅值递减的上下边带谐波。

实际上所有谐波的角频率都可以写成以下通式：

nω_c±kω（5-5）

式中，n和k均为自然数。

对于双极性SPWM而言，有以下结论：

（1）在载波比足够大、调制比小于1的时候，基波成分与调制波信号成线性关系。

（2）不含偶数次载波谐波。

（3）不含k+n为偶数次的边带谐波。

（4）谐波出现在载波频率整数倍频率附近。

2.单极性SPWM技术

1）单极性SPWM的基本原理

单极性SPWM技术的基本原理图如图5-6所示。与双极性SPWM方式相同，调制信号u_m为正弦波，重复周期为T，幅值为U_m；载波信号u_c采用单极性不对称三角波如图5-6所示，其重复频率为f_c，幅值为U_cm。u_c和u_m的交点可决定u_g2和u_g3的占空比D，改变U_m即可改变u_m与u_c的交点，从而改变占空比D。

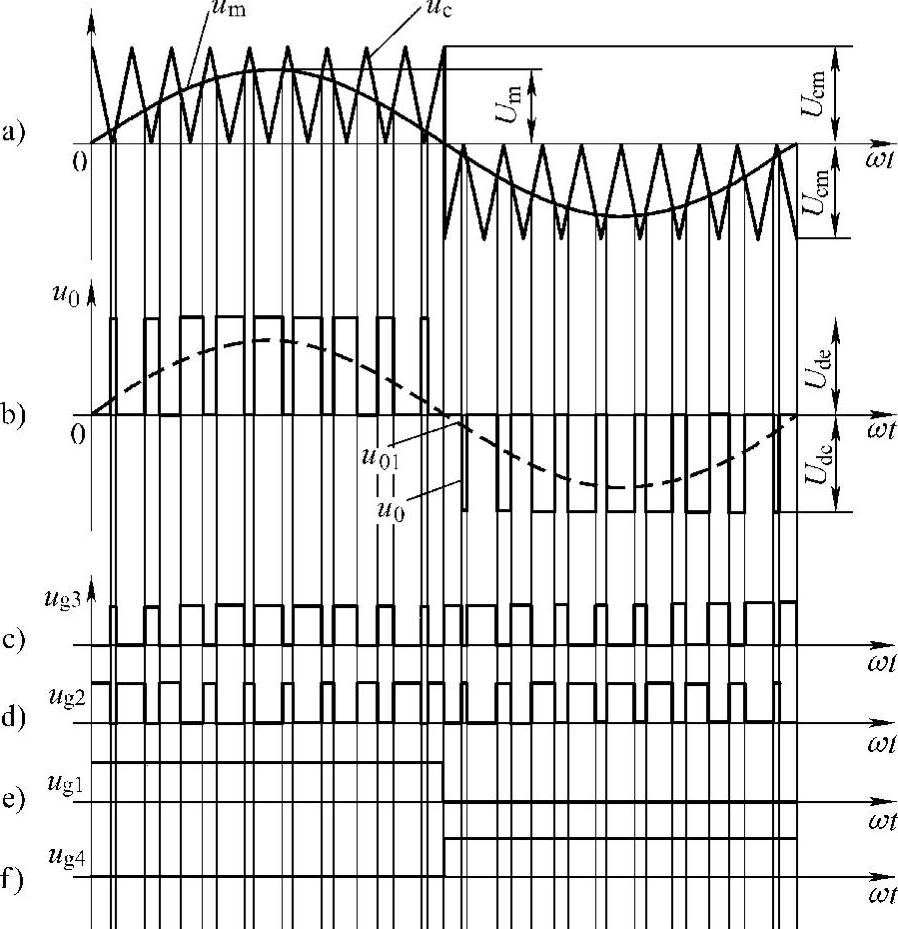
图5-6 单极性SPWM单相逆变电路的电量波形

载波u_c在调制波u_m的正半周为正极性的三角波，在负半周为负极性的三角波。调制信号u_m为正弦波。在u_c和u_m的交点时刻控制VI₃或VI₄的通断。在u_m的正半周，VI₁保持导通，当u_m>u_c时，使VI₄导通，负载电压u₀=U_dc，当u_m<u_c时，使VI₄关断，u₀=0；在u_m的负半周，VI₁关断，VI₂保持导通，当u_m<u_c时使VI₃导通，负载电压u₀=-U_dc，当u_m>u_c时，使VI₃关断，u₀=0。这样，就得到了SPWM波形u₀。图5-6b中虚线u₀₁表示u₀中的基波分量。像这种在u_m的半个周期内三角波载波只在一个方向变化，所得到的PWM波形也只在一个方向变化的控制方式称为单极性PWM控制方式。输出电压u₀波形如图5-6b所示。由于VI₂和VI₃是高频斩波开关，习惯上称为斩波臂；VI₁和VI₄是基波频率开关，习惯上称为控制臂。

2）单极性SPWM逆变器输出电压谐波分析(www.daowen.com)

图5-7所示是m=0.8，K=15时单极性SPWM的频谱。对单极性SPWM而言，有以下结论：

（1）基波成分与调制波信号成线性关系；

（2）不含载波谐波；

（3）不含k为偶数次的谐波；

（4）谐波出现在载波频率附近。

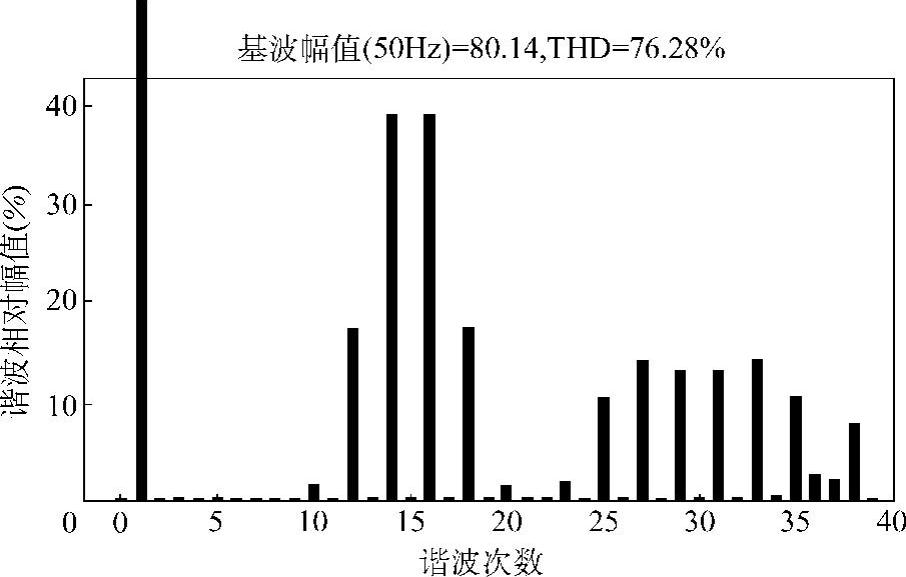
图5-7 单极性SPWM逆变器m=0.8，K=15时，输出电压频谱

3.倍频式SPWM技术

1）倍频式SPWM的基本原理

在普通PWM逆变电路中，器件开关频率与输出电压载波频率相等，所谓倍频式PWM逆变电路是指输出电压等效载波频率f_cp是逆变器件开关频率f_c的2倍。倍频技术能够缓解谐波抑制与效率提高之间的矛盾，且其实现仅需要适当安排逆变器件控制信号的时序，因而是很有使用价值的技术。

倍频式SPWM的工作原理如图5-8所示。由图可见，与普通单极性SPWM逆变器的差别是包含两个载波信号u_c1和u_c2，且有u_c1=-u_c2。正弦波调制信号u_m与u_c1的交点形成相位互补的脉冲序列u_g1和u_g4；u_m和u_c2的交点形成另一对互补脉冲序列u_g2和u_g3。在输出电压u₀的正半周，实际上是再现信号u_g1和u_g3的与逻辑；当u_g1与u_g3同处高位时，有VI₁和VI₃导通，u₀=U_dc；当u_g1或u_g3中有处于低位时，例如u_g3为低位（u_g2为高位），则有VI₁和VI₂导通，u₀=0。由于在正半周中，u_g1的高位区恒宽于u_g3，故其与逻辑可视为u_g1的两缘而输出电压u₀的脉宽也就是u_g1对u_g3的双缘，因而这种控制也称双缘调制。由于u_g1和u_g3的与逻辑在一个载波周期T_c（T_c=1/f_c）中共有两次状态转换，故输出电压u₀的电平也有两次变化，但对逆变桥中器件而言却只有开关一次；同理可分析u₀的负半周。

2）倍频式SPWM逆变器输出电压谐波分析

图5-9所示是m=0.8，K=15时倍频式SPWM的频谱。

对倍频式SPWM而言，有以下结论：

（1）基波成分与调制波信号成线性关系；

（2）不含载波谐波；

（3）不含偶数次谐波；

（4）谐波出现在载波频率偶数倍频率附近。

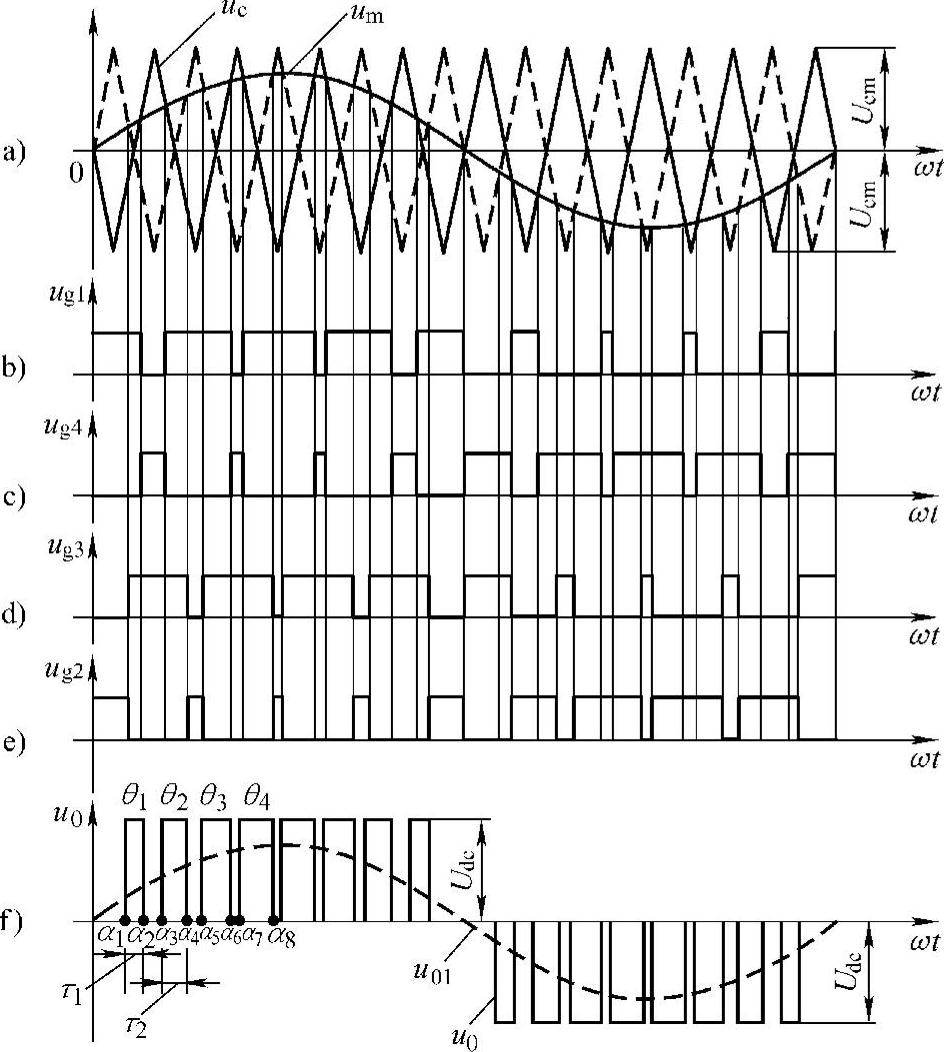
图5-8 倍频式SPWM单相逆变电路的电量波形

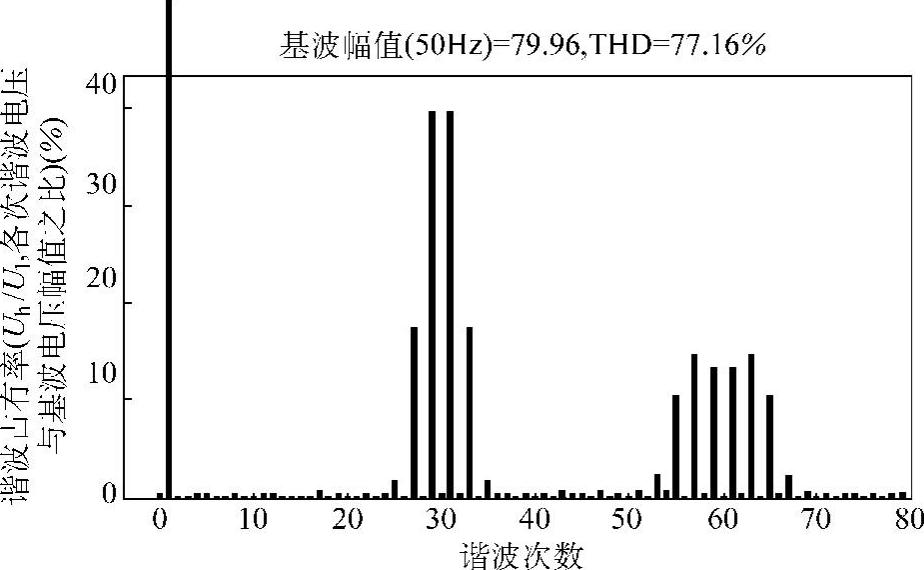
图5-9 倍频式SPWM逆变器m=0.8，K=15时，输出电压频谱

4.各种SPWM的技术分析与比较

1）频率和谐波分析

表5-1列出了在相同载波频率ω_c下，上述各种SPWM方法应用于单相全桥电路时各自的总开关频率ω_VI（即所有器件开关频率的和）、输出电压脉动频率ω_o以及最低次谐波群中心频率ω_h。此外，还给出了总开关频率与输出电压脉动频率的比值k=ω_VI/ω_o。

表5-1 各种SPWM方法的相关参数比较

从表5-1可以看出，当载波频率相同时，双极性SPWM的总开关频率比单极性SPWM高几乎一倍（因为一般有ω_m<<ω_c），因此总开关损耗也大一倍；而从图5-5、图5-7的波形频谱中也可以看出，双极性SPWM在相同幅度调制比的情况下，谐波特性比单极性SPWM的差很多。当载波频率相同时，倍频式SPWM的总开关频率比单极性几乎高一倍，但其输出电压的脉动频率也相应高了一倍；从总开关频率与输出电压脉动频率的比值k上可以看出，倍频式SPWM与单极性SPWM的k基本相等。图5-10给出的是输出脉动频率和调制比相同时，3种SPWM输出电压波形的频谱图（其中输出脉动频率为1200Hz，调制比为1）。

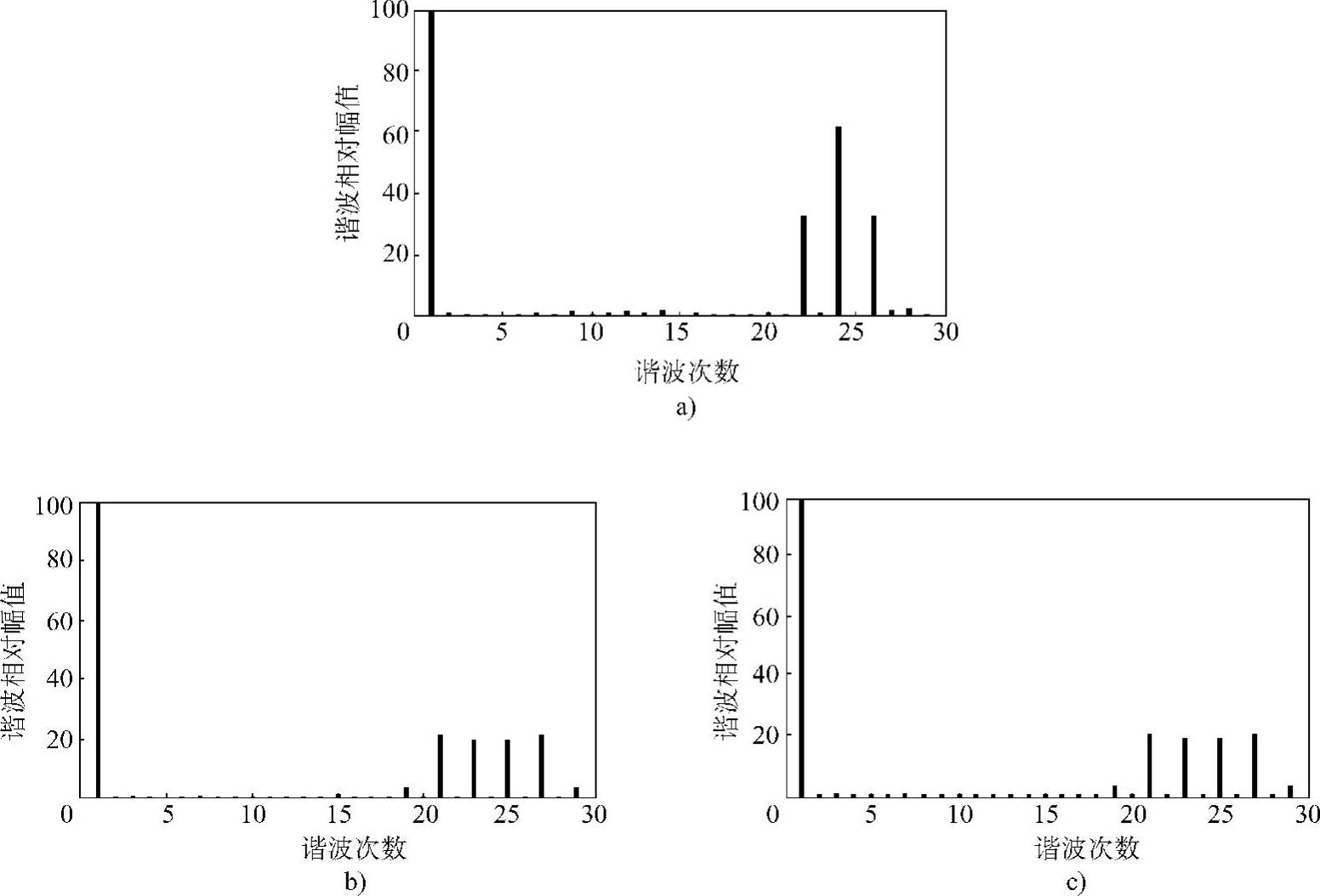
图5-10 3种SPWM输出电压波形频谱分析

a）双极性SPWM输出电压频谱 b）单极性SPWM输出电压频谱 c）倍频式SPWM输出电压频谱

从图5-10b和图5-10c可以看出，当输出电压脉动频率相等时，倍频式SPWM的谐波特性与单极性SPWM完全相同。

表5-2给出了在相同输出电压脉动频率（以1200Hz为例）和相同幅度调制比（以m=1为例）的情况下，各种SPWM方法下单相全桥逆变器输出电压的总谐波畸变率（Total Harmonic Distortion，THD）。从表5-2可以看出，双极性SPWM的THD最大，倍频式SPWM和单极性SPWM的THD基本相当。从通过以上分析可以看出，对于单相全桥电路而言，从总开关频率、输出电压脉动频率和谐伯德性几方面综合考虑，倍频式SPWM和单极性SPWM是比较适合的方法。

表5-2 相同输出电压脉动频率和幅度调制比下单相全桥逆变器输出电压的THD（分析到60次谐波）

2）开关应力和热稳定性分析

前文的讨论只着重于频率特性和谐伯德性，下面对开关应力及热稳定性进行讨论。对于双极性SPWM和倍频式SPWM而言，各开关器件的开关频率完全一致，开关应力也完全相同，各器件的热稳定性也相同。对于单极性SPWM则有所不同。在单极性SPWM单相逆变电路中，斩波臂高频开关，开关应力高，器件的损耗主要表现为开关损耗；控制臂基频开关，开关应力低，器件的损耗主要表现为通态损耗。由于斩波臂与控制臂的开关应力不一致，器件损耗性质不同，器件的热稳定性很难保持一致，严重的时候会出现热不平衡现象，尤其是斩波臂的开关频率较高的时候。因此采用单极性SPWM时，器件选择和散热器设计会成为一大问题。为了解决单极性SPWM的热不平衡问题，出现了一种改进的单极性SPWM方式，即在正弦波的正半周期，VI₁与VI₄组成斩波臂，而VI₂与VI₃则处于常断或常通状态；在正弦波的负半周期，VI₂与VI₃变为斩波臂，而VI₁与VI₄则处于常断或常通状态。这样，各器件的开关应力就达到了基本平衡，热稳定性也趋于一致。