从图2-16中可以看出：参与合成的阶梯数越多，即N越大，阶梯波越接近于正弦波，阶梯波中的谐波含量也就越小。N个不同相位和不同幅值的方波或矩形波电压的叠加，可以做到某些低次谐波相互抵消，使阶梯合成波中的谐波含量达到最小。这就是“谐波抵消”理论。

基于“谐波抵消”理论的合成阶梯波含有的谐波次数为

H=2kN±1（2-61）

式（2-27）中，k=1、2、…、∝，N为单相功率电路的个数。因此，N越大，阶梯数就越多，阶梯波的谐波含量也越小。

下面将以方波合成阶梯波和矩形波合成阶梯波两种情况，来说明“谐波理论”在合成阶梯波时的应用。

阶梯波越接近理想的正弦波，其谐波总含量就越小。将正弦波在半个周期内沿x轴分成N个相等的间隔，取正弦波在此间隔内的平均值，即为这一间隔内阶梯波的阶高。设正弦波方程为

u_o=U_msinωt（2-62）

式中 U_m——正弦波电压幅值；

ω——正弦波电压角频率。

则第i个阶高为

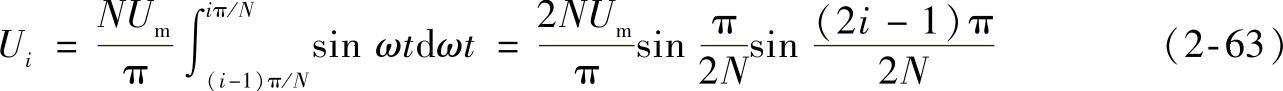
对阶高满足式（2-63）的阶梯波，通过傅立叶级数展开式求得其所含谐波次数为2kN±1，这是阶梯波中谐波含量最小的情况。

一般情况下，当合成一个周期的阶梯波需要方波电压的个数为奇数时，应取第一个方波与阶梯波同相，其余的方波左右对称成对组合，每对方波的幅值相等，第一对组合的方波与阶梯波的相位差为±π/N，第二对组合的方波与阶梯波的相位差为±2π/N……，依次类推。这样，从阶梯波半个周期来看，第一个方波在0～π期间都被叠加；第一对组合方波在π/N到（N-1）π/N的期间内被叠加，其余期间相互抵消；第二对组合方波在2π/N到（N-2）π/N的期间内被叠加，其余期间相互抵消；依次类推，便可求得各方波电压的幅值与阶梯波阶高的关系。

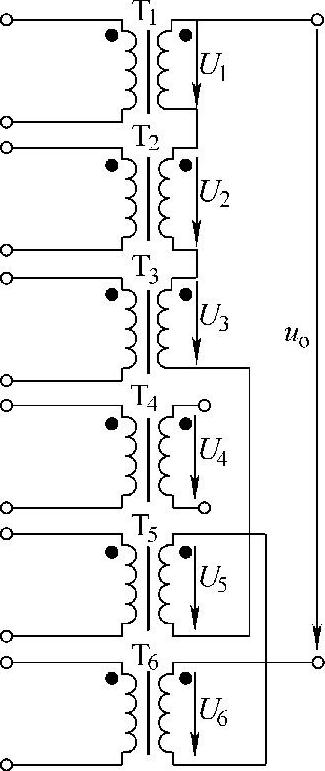
图2-18 阶梯波合成逆变器的电路结构及N=6时原理波形

以N=6为例，从式（2-63）可知如何由阶高决定各单相方波的幅值。设U₁～U₆为依次相移π/6=30°的方波，如图2-18所示，取U₁与阶梯波同相，φ₁=0°，其他各方波U_i与阶梯波相位差ϕ_i=（i-1）180°/N。图中U₂、-U₆与阶梯波相位差±30°，U₃、-U₅为±60°。从阶梯波半个周期看，U₁在0～π之间都起作用；U₂、-U₆只在π/6～5π/6期间被叠加，其余期间相互抵消；U₃、-U₅则在2π/6～4π/6期间被叠加，其余期间相互抵消。这样，很容易求得各方波电压幅值与阶高的关系。

假设方波电压U₁～U_i的幅值为U_{1 m}～U_{i m}，将N=1代入式（2-63），则方波电压U₁的幅值U_1m为

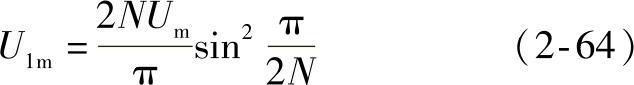
由式（2-64）可得阶差的一般表达式为

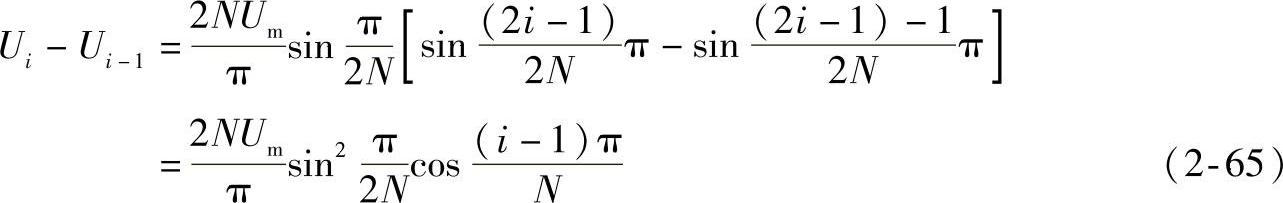
由式（2-65）可得，第i对组合方波的幅值为

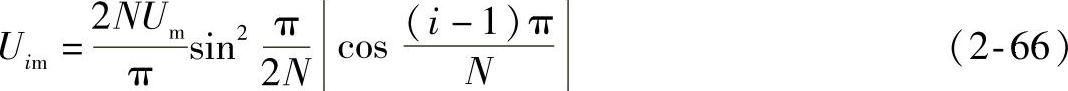
将阶梯合成波通过傅立叶级数展开，可以得到基波的幅值U_jm为

将式（2-67）代入式（2-32）中，得到第j个方波幅值的一般表达式为

在应用以上公式时，应注意以下各点：

（1）在式（2-67）中，U_m为在求阶高时所假设的正弦波的幅值，见式（2-64）。它是一个虚设的中间变量，而U_jm是阶梯合成波中的基波分量的幅值。在设计阶梯波合成逆变器时，将设计要求的输出正弦波电压的有效值视为U_jm，按照式（2-68）求出各阶方波电压的幅值。

（2）在运用式（2-68）时，应注意限制条件。即在推导式（2-68）时，曾假设阶梯波由奇数个方波电压合成，所以，式（2-68）仅适用于方波，而不适用于矩形波，且仅适用于阶梯波合成逆变器的输出绕组为奇数的情况。

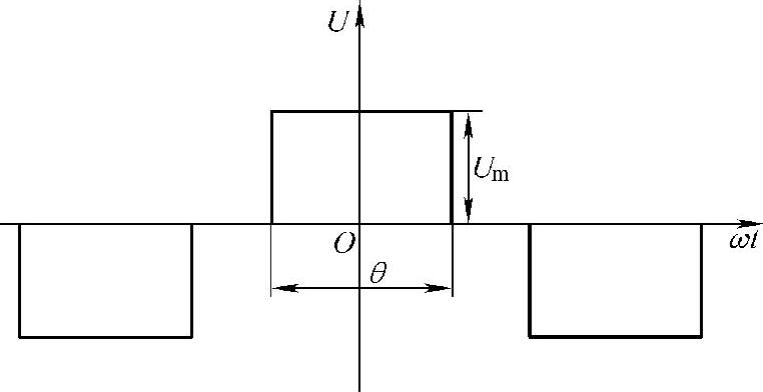
图2-19 矩形波波形(www.daowen.com)

矩形波的波形如图2-19所示，θ为矩形波的脉冲宽度，U_m为矩形波脉冲的幅值。在N个依次相移π/N的矩形波中，第i个矩形波的傅立叶级数的展开式为

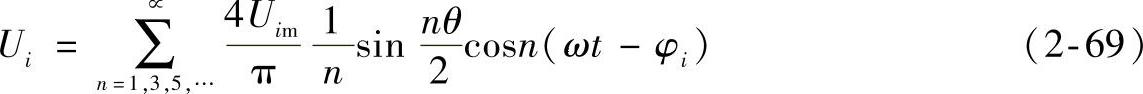
式中 φ_i——第i个矩形波U_i的初始相位角，φ_i=φ₁+（i-1）π/N；

φ₁——^第一个矩形波U₁的初始相位角；

U_im——第i个矩形波U_i的幅值。从图2-17中可以看出：U_im为第i个逆变器的输

出矩形波的幅值U_d与变压器电压比s_i的乘积，即U_im=s_iU_d。这样，U_i可写

成：

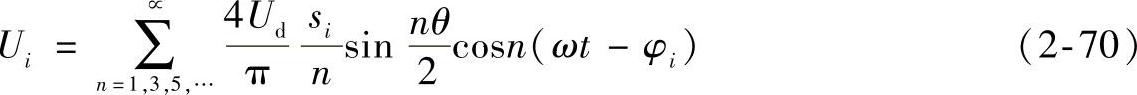
N个矩形波叠加后，得到阶梯合成波电压的表达式为

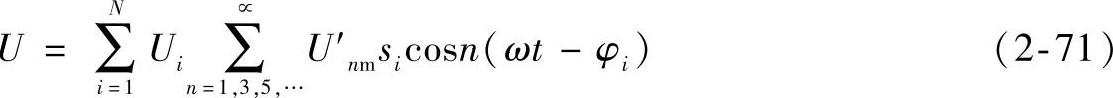
式中 U′_nm——阶梯波合成逆变器的变压器原边绕组电压中的第n次谐波电压U′_n的幅

值。

式（2-71）和式（2-70）相比较，可以得到

那么，第n次谐波电压U′_n可表示为

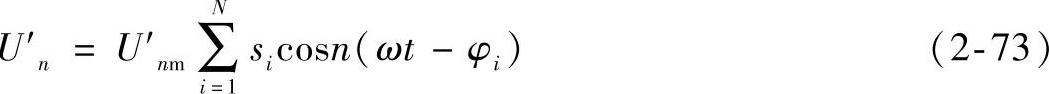
从式（2-73）可以看出，要消除第n次谐波，即要求U′_n=0，必须满足下列条件：

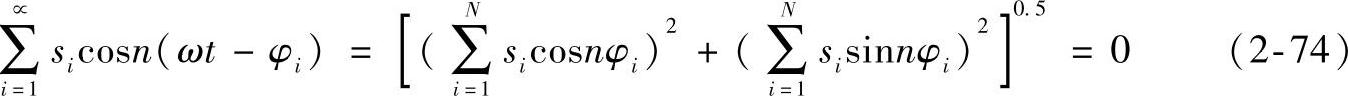
即

和

因为阶梯合成波含有的谐波次数为2kN±n，将2kN±n取代n代入式（2-74）中，可得到消除n次谐波的必要条件为

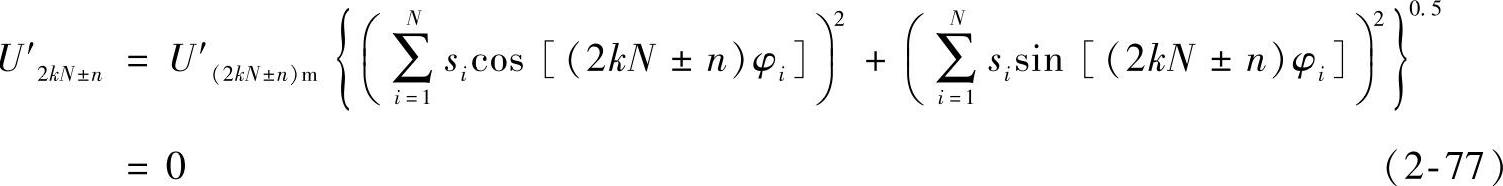
由于在k=1，2，…时有cos[（2kN±n）φ_i]=±cosnφ_i和sin[（2kN±n）φ_i]=±sinnφ_i。式（2-77）可推导为

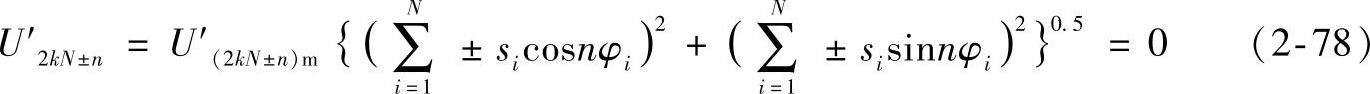
由于要保留阶梯合成波的基波分量，2kN±1次的谐波不能消除，即U′_2kN±1≠0。而要消除n次谐波时，要求U′_2kN±n=0。所以，在消除n次谐波时，2kN±n次谐波也一同被消除。例如，在阶梯数为12，即N=6时，若要消除3次谐波，即n=3，那么，除消除了3次谐波以外，2kN±3（k=1，2，…）所包含的各次谐波均被消除，如9，15，21，27，…次谐波被一同消除。而要消除5次谐波时，2kN±5（k=1，2，…）所包含的各次谐波，如7，17，19，29，…也一同被消除。

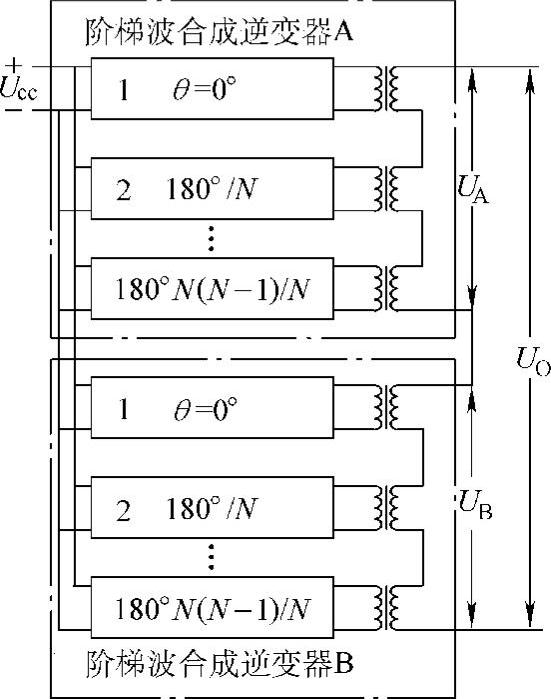
图2-20 移相调压式阶梯波合成逆变 器的电路结构