当逆变器负载为RLC且满足振荡条件时,这种负载称为谐振负载。谐振负载既可以是串联的,也可以是并联的。对于谐振负载,可以通过改变逆变频率来改变输出电压和功率,例如感应加热负载和中频X射线机高压逆变负载。因此,对输出频率没有严格要求,而又要求改变输出电压的场合,可以利用谐振式逆变电路来达到目的。
谐振式逆变电路的特点:
(1)逆变电路输出波形为方波(电压方波或电流方波)。
(2)对于这种负载,可以将逆变频率调谐到谐振频率附近,从而获得正弦的输出电流或电压,而无需通过低通滤波器来消除其最低次谐波,所谓“谐振”式逆变电路也因此而得名。
(3)谐振式逆变器的一大缺点是由于利用负载的谐振特点,电路中的元器件要承受很大的电流或电压。电力半导体器件会因此而需承受很大的器件应力。
谐振式逆变器有电压型串联谐振式和电流型并联谐振式两种。对于串联谐振式逆变器,其输出电压为方波,负载电流波形接近正弦波,而并联谐振式逆变器的输出电流为方波,负载的电压波形接近正弦波。
1.电压型串联谐振逆变电路
串联谐振槽路(RLC)如图2-6a所示。其导纳Y可表示为
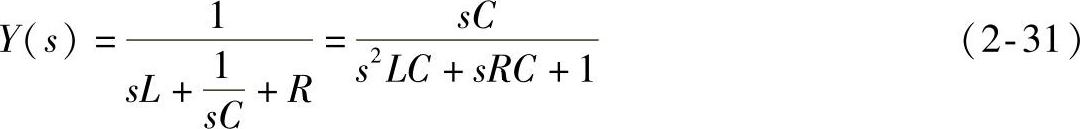
它是复频率s=jω的函数。若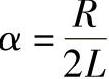 ,
,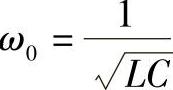 ,则有
,则有

由式(2-32)可知,谐振时,即s=jω0时,感抗和容抗互相抵消,Y(s0)=1/R,即电路阻抗为纯阻性质,频域的对数幅频特性如图2-6b所示。曲线的陡峭程度可用半宽度来描述,也就是半功率点或3dB点的频率范围。对于串联谐振式逆变器,3dB点出现在s=j(ω0±α)处,所以其半宽度为2α。
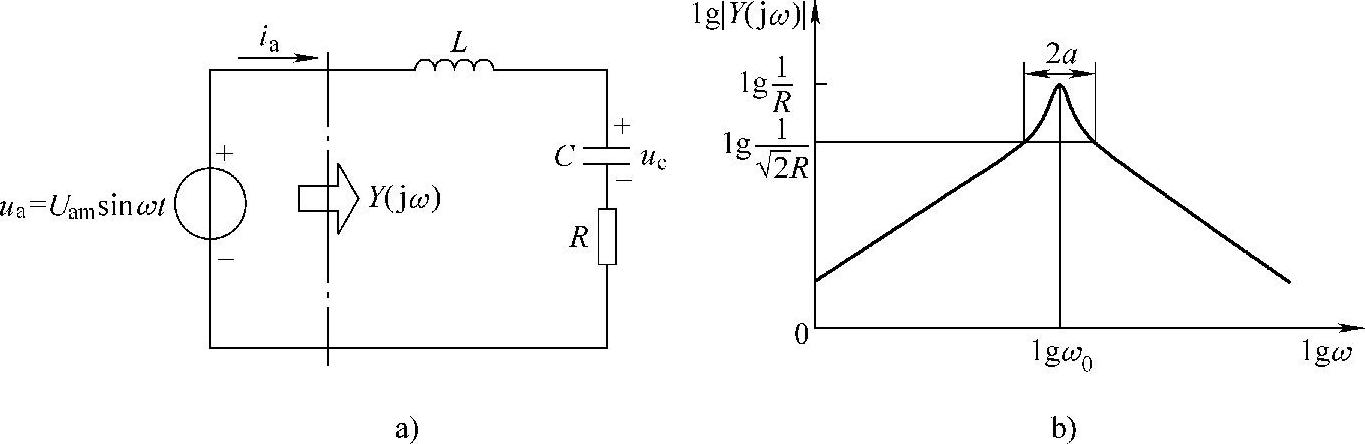
图2-6 串联谐振槽路及其频率响应
a)串联谐振槽路 b)频率响应
若令串联谐振电路的品质因数为

则式(2-32)可变为
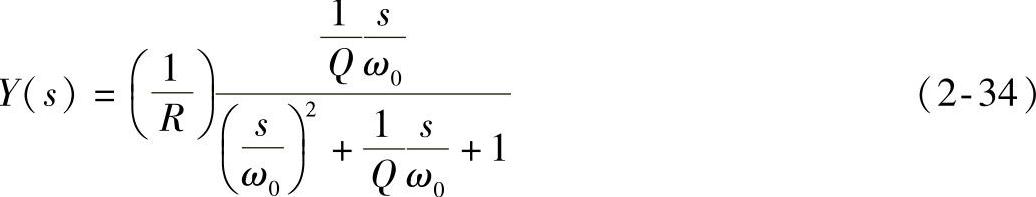
谐振时的特点:
(1)当s=jω0时,Y(s0)=1/R,也就是说,谐振时的负载(R)电压等于电源电压,即
uR=ua=Uamsin ω0t
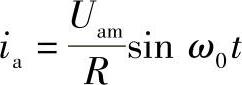
(2)电容和电感上的电压,可达电源电压的Q倍。在一般情况下,电路中电流ia可表达为Ia(s)=Ua(s)Y(s)
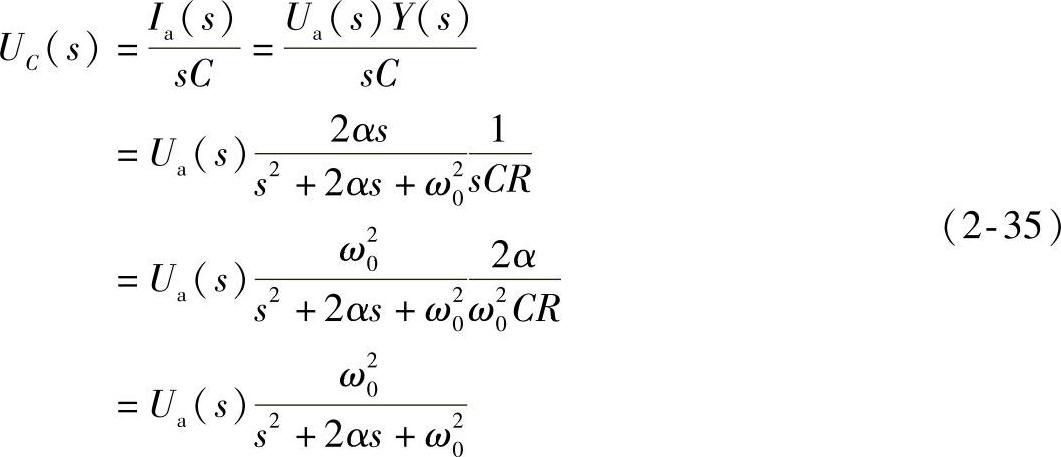
于是有

当s=jω0时

式(2-37)表明,谐振时电容(或电感)上的电压值正比于谐振电路的Q值,可比输入电源电压值高出许多倍。
前面所讨论的只是针对输入电源为正弦波的情况,加交流方波电压源的串联谐振电路示于图2-7a。
只要ω=ω0,而且Q值足够大时,则ia中所含的谐波分量很少,而且电流ia非常接近正弦波,故有
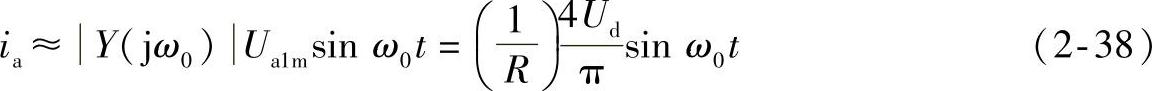
其中,Ua1m为方波电压的基波分量幅值,在这种情况下,谐振槽路电流ia与输入方波电压同相。在此处,我们看到利用电路的谐振性质来滤除谐波的例子,其波形示于图2-7b。
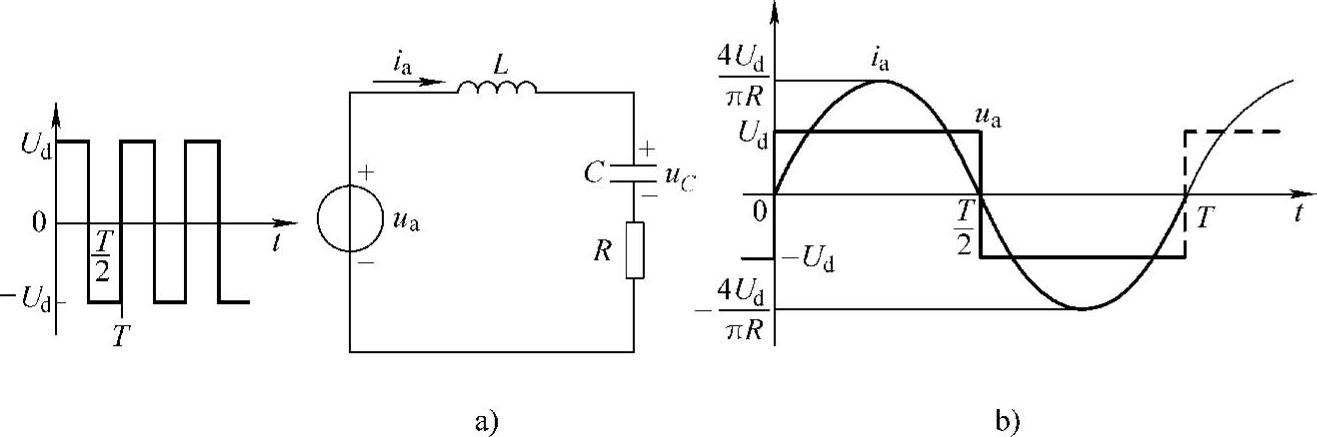
图2-7输入为方波电压的串联谐振电路及其波形
a)电路 b)波形
当电压源频率大于谐振频率,即ω>ω0时,LC作用相当于一个电感(LE),即

其中,β=ω/ω0>1。在这种情况下,谐振电路的阻抗等值于LR电路,如图2-8a所示,于是输入电源的基波电压ua1就加在LER上。若假定滤波器能将高次谐波滤除,使得ia≈ia1则有
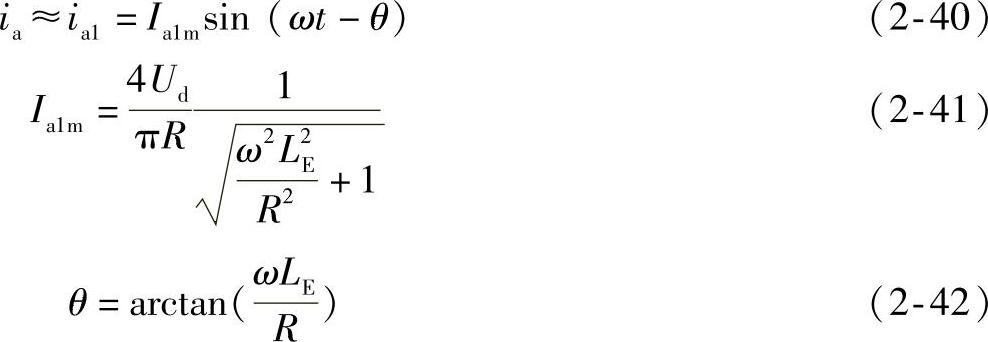
显然,在ω>ω0时,ia的幅值比ω=ω0时的小。其波形示于图2-8b。
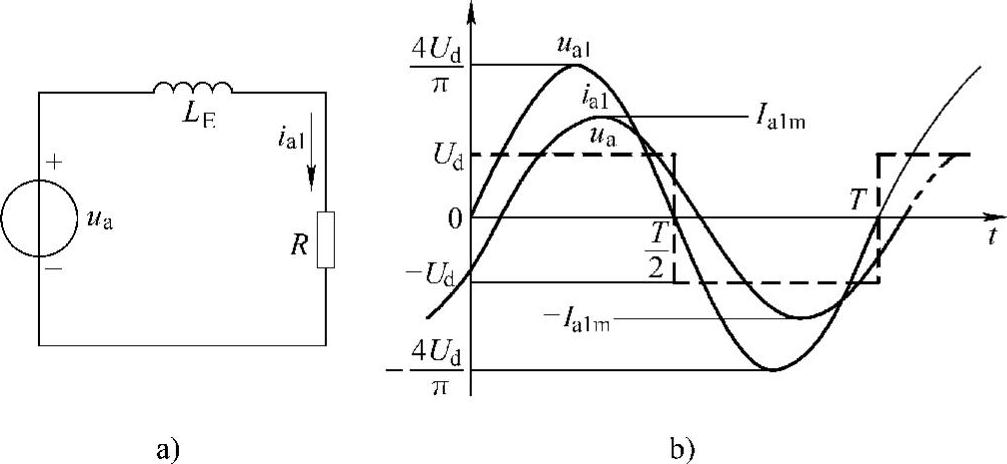
图2-8 ω>ω0时的等值电路及其波形
a)等效电路 b)波形
当ω<ω0时,LC的作用相当于一个电容(CE)即

其中,r=ω/ω0<1。此时的谐振电路阻抗等于RC网络,只要ω不是比ω0低得太多,仍足以使ia≈ia1,则有
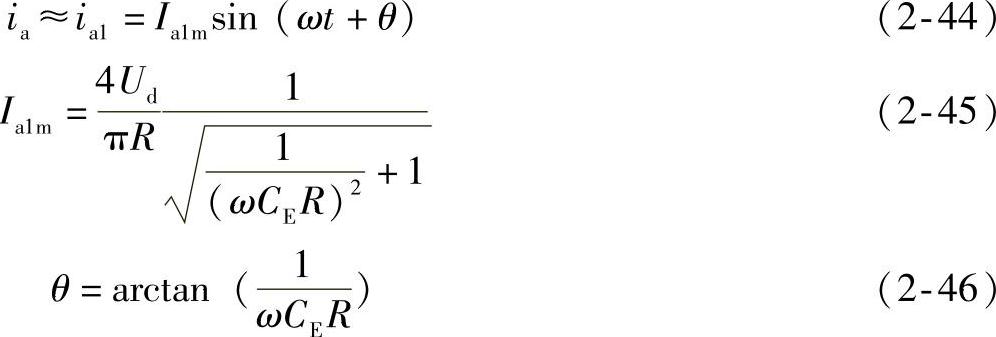
同理,ω<ω0时的ia幅值比ω=ω0时的小。其波形示于图2-9b。
从上面分析可知,只要电源频率(ω)偏离槽路的谐振频率(ω0),在附加阻抗上就引起了电压降落,因此负载(R)上的电压就要减少。当槽路的Q值比较大,这种偏离将会引起负载上电压大的变化。也就是说,可以通过改变逆变器的工作频率来改变负载上的电压和功率,即所谓调频调压和调频调功。
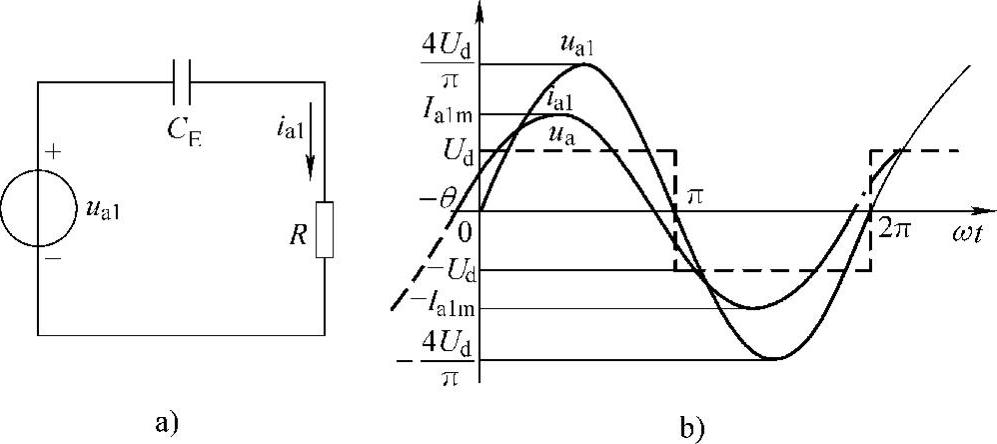
图2-9 ω<ω0时的等值电路及其波形
a)等效电路 b)波形
电压型串联谐振式逆变电路如图2-10所示,利用该电路,使VI1和VI2轮流工作半个逆变周期,则在串联谐振槽路的端口获得交流方波电压。
当逆变电路工作在谐振频率(ω0)时,开关器件的状态转换总是发生在开关器件电流过零的时刻,因而降低了器件的开关损耗(见图2-7b)。在这种情况下,所有反并联二极管始终不通过电流。
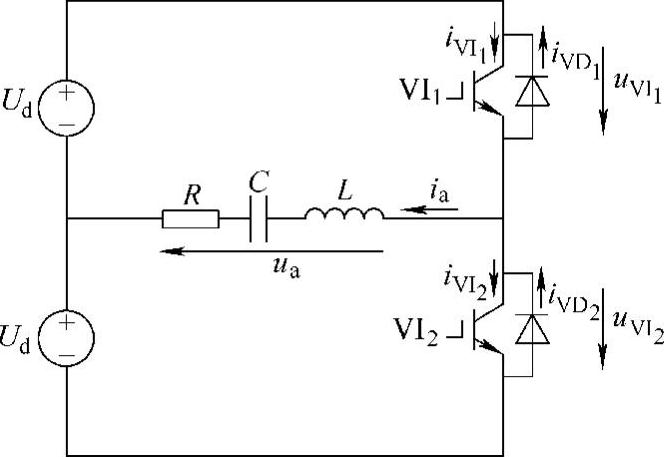
图2-10 电压型串联谐振式逆变电路(半桥)
当逆变电路的工作频率大于谐振频率,即ω>ω0,且ω≈ω0时,电路工作于感性负载条件下,负载电流ia滞后于槽路端口电压ua,如图2-11a所示。
当逆变电路的工作频率小于谐振频率,即ω<ω0,且ω≈ω0,谐振槽路呈现容性,所以负载电流ia超前于槽路端口电压ua,如图2-11b所示。(www.daowen.com)
2.电流型并联谐振逆变电路
并联谐振槽路示于图2-12a,其中,ia为正弦波。其导纳可表示为
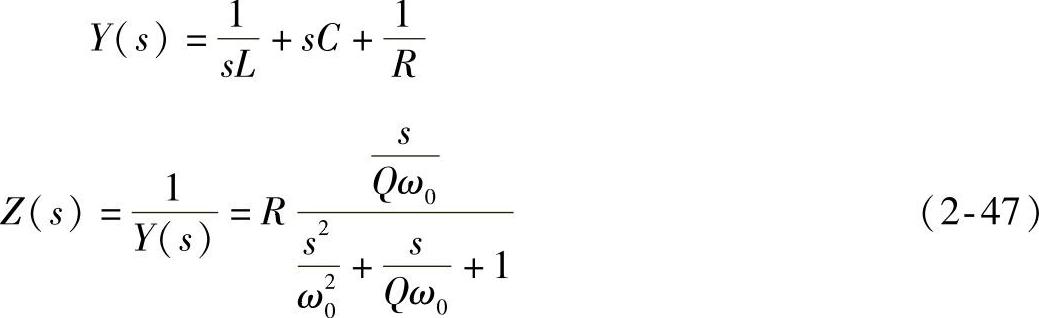
式中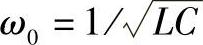 ,令
,令
Q=ω0RC(2-48)
比较式(2-47)和式(2-32)可知,二者形式相近,只是系数不同,因此它们的幅频特性曲线的形状是一样的。图2-12b给出了并联谐振槽路的对数幅频特性。同串联谐振一样,其半宽度为2α,可用以表征曲线的陡峭程度。
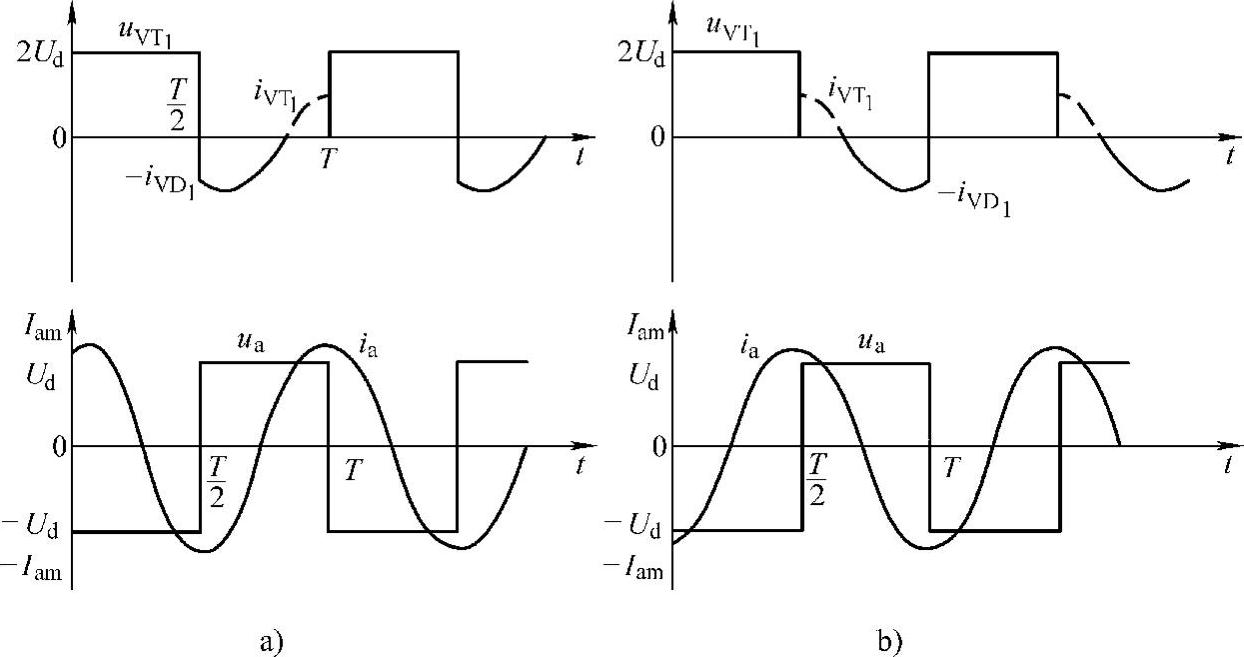
图2-11 电压型串联谐振式逆变电路工作波形
a)ω>ω0 b)ω<ω0
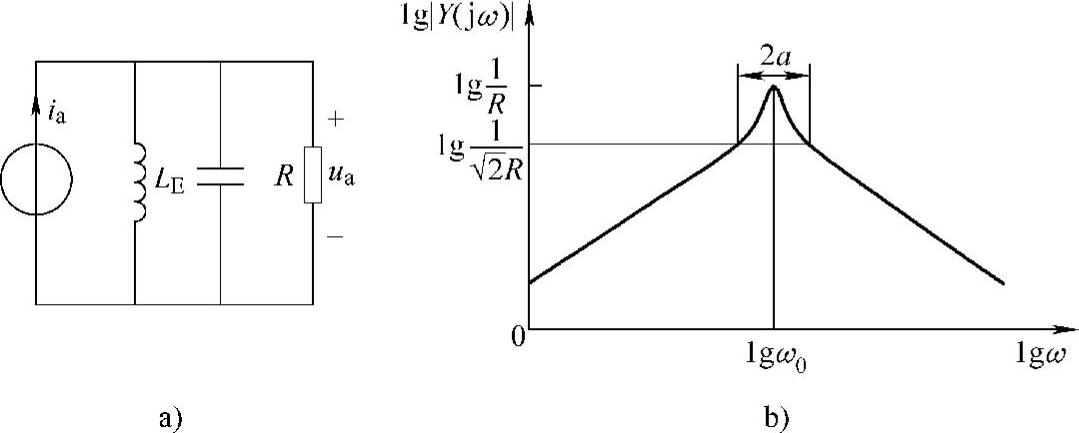
图2-12 并联谐振槽路及其频域响应
a)并联谐振槽路 b)对数幅频特性
谐振时的特点:
(1)当s=jω时,Z(s0)=R。也就是说,谐振时负载R中的电流就等于电流源的电流ia=Iasinωt,LC并联槽路相当于开路,但L和C中都流过很大的电流。这时,整个并联槽路的阻抗为纯阻性质。
(2)通过电容和电感的电流为电流源电流的Q倍。谐振时,槽路的电压为
所以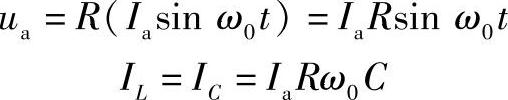
即
前面讨论的是电流源为正弦波的情形。方波电流输入的并联谐振槽路示于图2-13a,并分下述几种情况加以讨论。
1)在ω=ω0,即电流源频率(ω)等于谐振频率(ω0)时,只要Q值足够大,槽路电压ua中所含的谐波很低,则可以认为
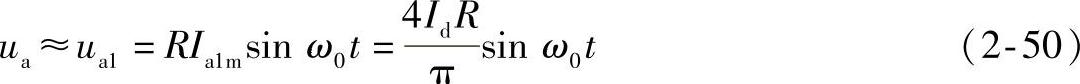
其波形示于图2-13b。负载电压ua同输入电流ia同相,槽路显示电阻性。
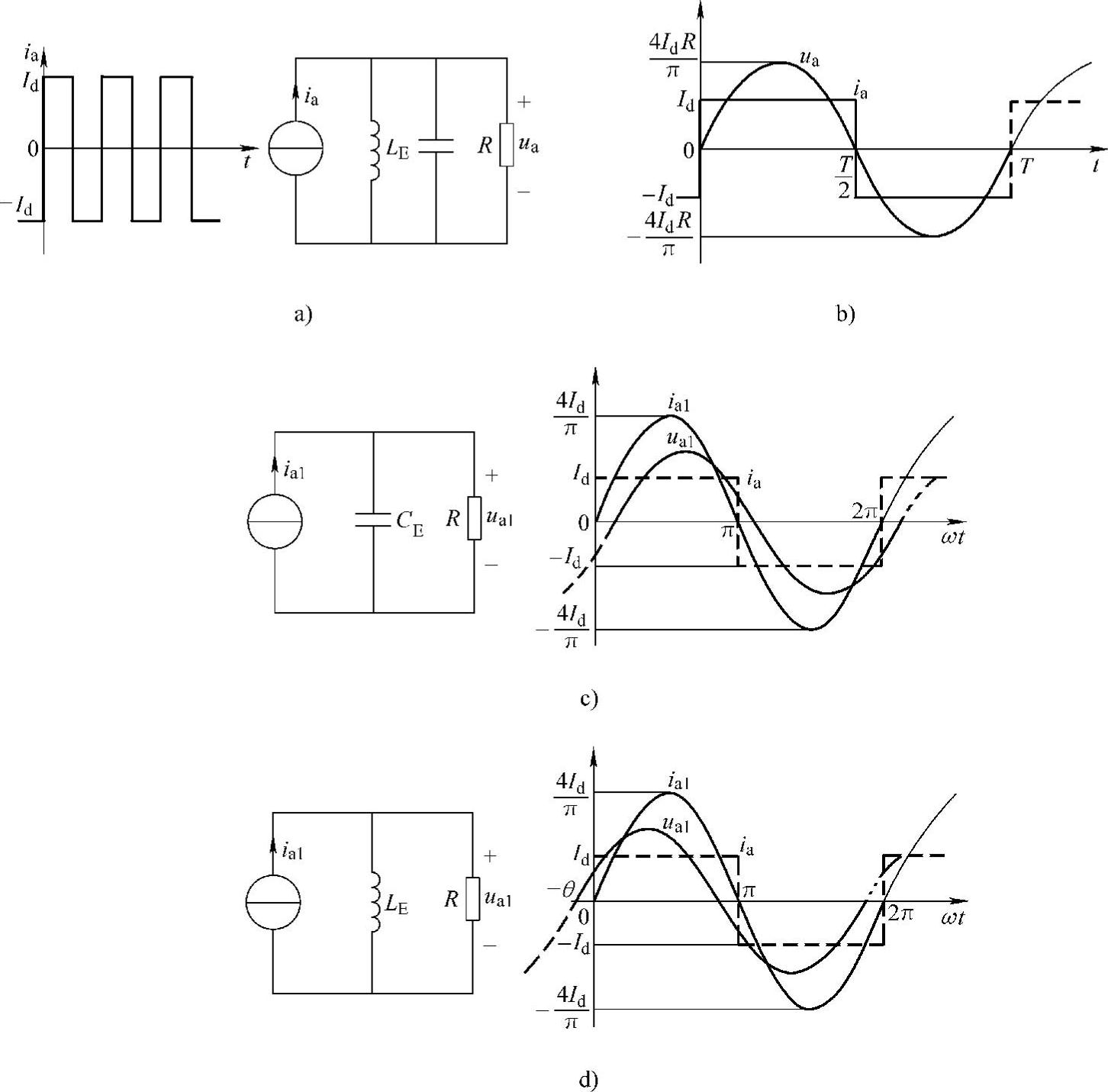
图2-13 方波电流输入的并联谐振槽路及其波形
a)电路 b)ω=ω0的波形 c)ω>ω0的波形 d)ω<ω0的波形
2)当ω>ω0时,LC槽路的作用相当一个电容CE,它同负载电阻R相并联,起分流作用(见图2-13c)。这样一来,流过R的电流减少,槽路电压ua1也降低。因整个槽路显容性,槽路电压ua1滞后于ia,其波形如图2-13c所示。
3)当ω<ω0时,LC槽路的作用相当一个电感LE,它也是同电阻R并联,也起分流作用。因此,流过R的电流也减少,槽路电压ua1也同样降低。因整个槽路呈感性,槽路电压超前于ia,其波形如图2-13d所示。
很显然,同串联谐振一样,通过改变输入频率可以改变并联槽路的电压,从而也就改变了负载的功率。当然,实际应用时,频率改变范围受下面三个因素的限制:器件开关频率、元件的电流容量以及最低次谐波频率不得接近槽路的谐振频率。
电流型并联谐振式逆变电路示于图2-14。利用该电路,使VI1、VI4同VI2、VI3轮流工作半个逆变周期,则可在并联谐振槽路端口获得交流方波电流。
当逆变电路工作在谐振频率(ω0)时,同串联谐振电路类似,开关器件的状态转变总是发生在器件电压过零时刻(见图2-13b),从而降低了器件的开关损耗。
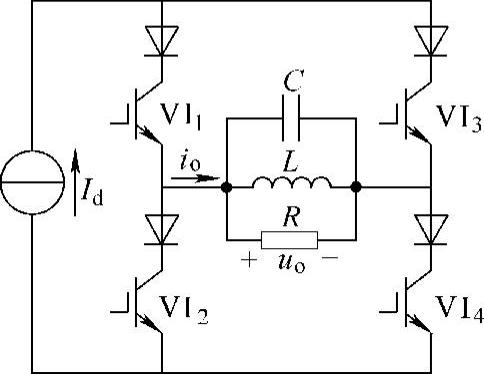
图2-14 电流型并联谐振式逆变电路
由图2-13c可知,当ω>ω0且ω≈ω0时,电路工作于容性负载条件下,负载的电压ua1滞后于ia。
当ω<ω0且ω≈ω0时,电路工作于感性负载条件下,负载的电压ua1领先于ia(见图2-13d)。在这种条件下,当一对开关管导通时,另一对开关管就立刻加上正向电压。对于IGBT开关来说,可将需关闭的那对器件的触发信号置低,让其关断后,再触发需要导通的那一对器件。
3.串并联复合型谐振逆变电路
串并联复合型谐振全桥逆变器如图2-15所示,谐振电路的输入电压uDS2是幅值为Ud的交流方波:
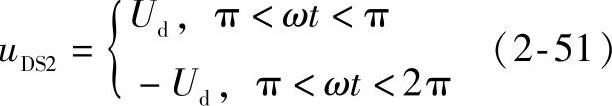
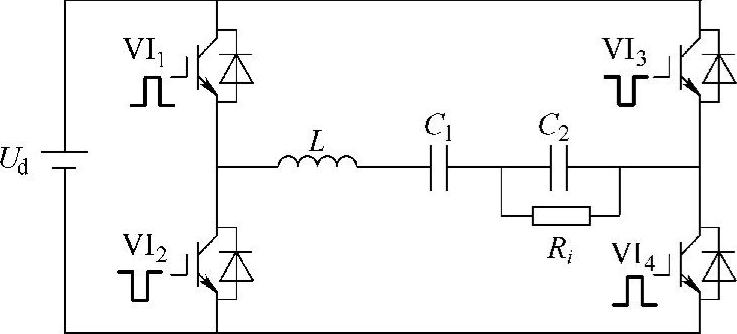
图2-15 全桥串并联谐振逆变器
其基波成分为ui1=Umsinωt,这里,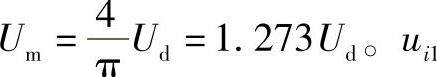 的有效值为
的有效值为
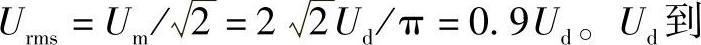
谐振电路输入基波分量的传递关系为
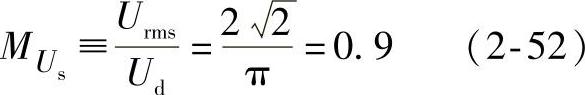
由于串并联谐振环节的传递函数为
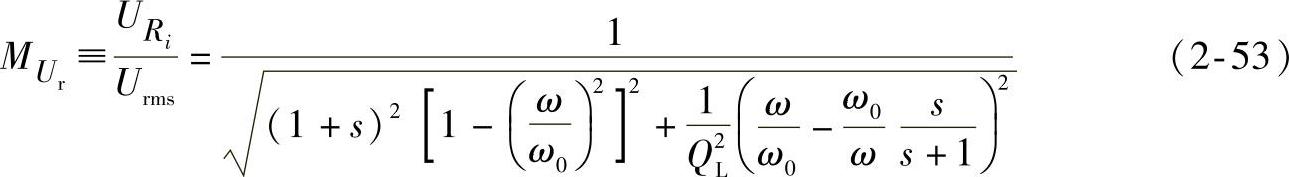
式中,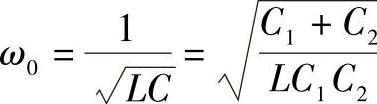 ,
,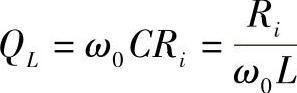 ;则由式(2-52)和式(2-53)得串并联谐振逆变器幅值传递函数为
;则由式(2-52)和式(2-53)得串并联谐振逆变器幅值传递函数为
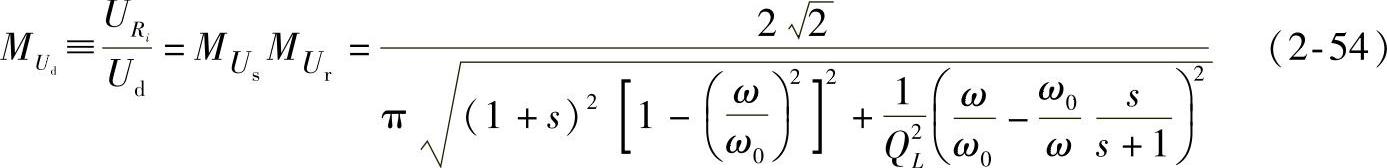
电感L的电流为i=Imsin(ωt-ψ),谐振槽的输入阻抗:
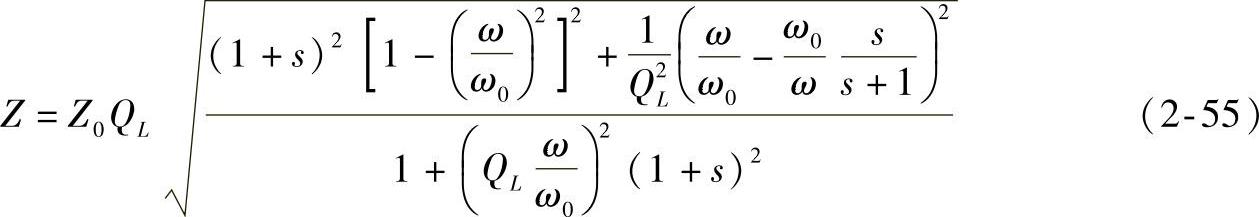
其中,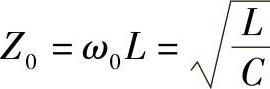 ,则电感电流为
,则电感电流为
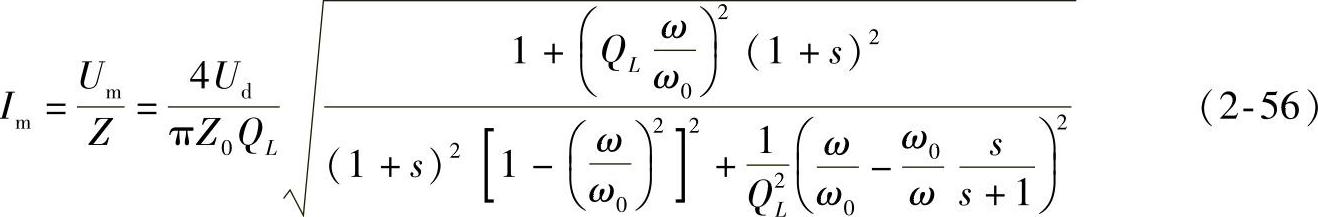
谐振电感两端电压为
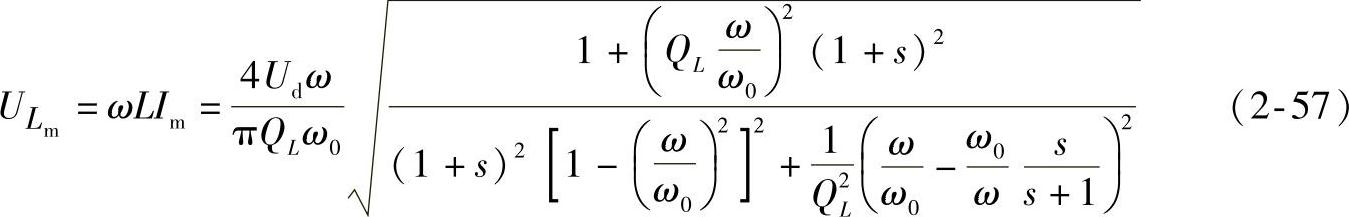
谐振电容C1的电压为
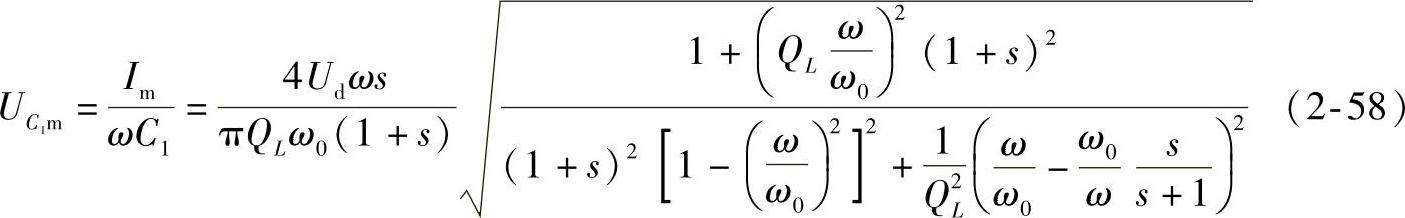
谐振电容C2的电压与逆变器输出电压相同:
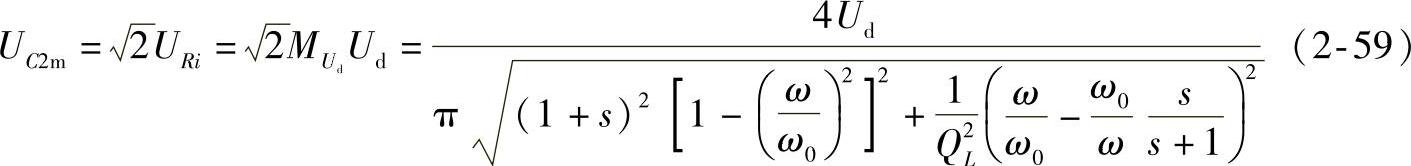
逆变器输出电流幅值为
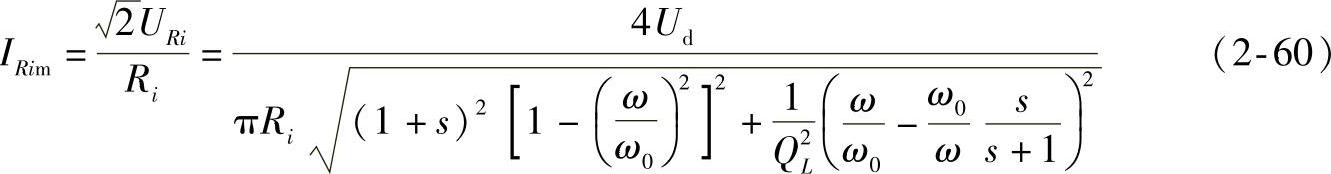
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





