1.基本假定
(1)构成逆变电路的功率开关器件均为具有理想特性的器件:无惯性、无内耗、开关状态的切换可在瞬间完成。
(2)向逆变电路供电的直流电源无内阻,直流侧并联电容值足够大,直流电压无纹波,且不受负载影响。
(3)逆变电路具有理想负载,变压器和电抗器无直流内阻、铁心无饱和;电路无分布电感和寄生电容;负载电容无内部损耗。
2.基本电路
电压型单相半桥式逆变电路如图2-1a所示,而单相全桥式逆变电路则如图2-1b所示。单相方波逆变是指逆变电路输出电压为交变方波,且脉宽τ=πrad,如图2-1d所示。由图可见,若加到全桥电路各桥臂可控器件VI1~VI4的控制极信号波形如图2-1c所示,即ug1和ug3、ug2和ug4同相;而ug1和ug4、ug2和ug3的相位互补,根据上述假定,电路输出电压uo波形为一交变方波,其脉宽τ=π。
按以上分析,逆变电路输出电压的重复频率,受控于控制极信号ug的重复频率f,输出电压uo的脉宽τ为π,脉冲幅值为Ud,如图2-1d所示。将uo用傅立叶级数展开,得
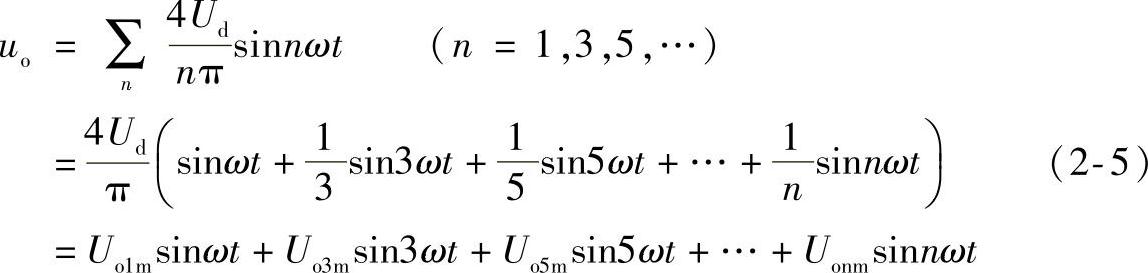
式中 ω=2πf。
Uo1m——输出电压基波幅值

Uo1——输出电压基波有效值

AV——输出基波电压增益

通过以上分析,可以看出方波逆变电路输出电压具有以下特点:
(1)输出电压uo的波形与负载无关,恒为交变方波,这是所有电压型逆变电路的共同特点;但输出电流io的波形则与负载性质和参数有关,例如在无源线性感性负载下,其基波分量io1滞后于基波电压uo1,其相位差ϕ1=arctanωLo/Ro。
(2)uo除包含基波分量uo1外,还包含奇次谐波,其幅值随谐波次数的增加而递减。令
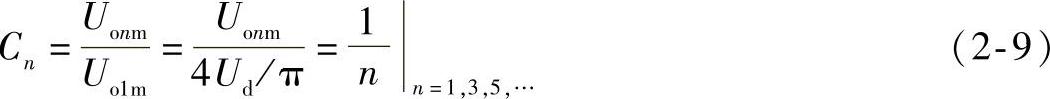
式中 Uonm——n次谐波幅值;
Cn——各次谐波的相对幅值。
显然,Cn越高,则表示uo的谐波含量越高。uo的总谐波畸变率(Total Harmonic Dis- tortion Factor,THD)定义为
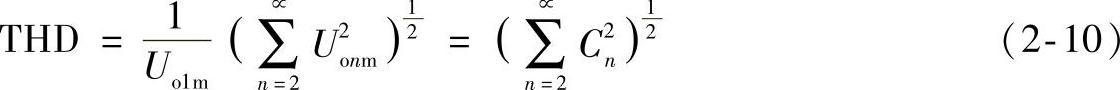 (https://www.daowen.com)
(https://www.daowen.com)
上式表明,THD也反映uo的谐波含量,若uo无谐波,则THD=0;逆变电路THD的容许值与负载有关,例如,计算机用不间断电源(UPS)的THD≤5%,这显然低于以交流电动机为负载的变频电源。
(3)电压增益AV表示输出基波幅值Uo1m与直流电压Ud之比,AV值越高,表示单位直流电压获得的交流电压Uo1m也越大,故AV又称为直流电压利用率。
由图2-1g可见,当VI1、VI3或VI2、VI4导通时,输出电压uo和输出电流io同向,电源向负载提供能量;当VD1、VD3和VD2、VD4导通时,输出电压uo和输出电流io异向,负载中能量反馈到Cd中,反并联二极管和Cd为无功电流提供通路。根据上述工作状态,逆变电路具有以下两种不同的换流方式。
(1)臂内换流:指电流在同一导电桥臂内器件间的转移。例如在图2-1e中,ωt=θ1时,iVD1=0,VD1截止,由于ug1>0,VI1相继导通,负载电流反向,并从VD1中转移至VI2(同理在另一桥臂中,有VD3移至VI3)。这种电流转移产生于电流过零时刻,换流过程只涉及桥臂内器件的更迭,并不改变导电回路,物理过程相对简单,故也称为自然换流方式;
(2)臂间换流:指电流在桥臂间转移。例如在ωt=θ2时,有ug1=0,VI1关断,由于iVI1=io>0,为了维持电流的原来的流向,尽管此时有ug2>0,但只有VD2正偏导通(由于VD2导通,VI2反偏阻断)。这种换流是在上下导电臂间进行,涉及导电回路的更迭,而且换流时退出导通的器件中的电流并无自然过零的性质,因而换流过程相对复杂,也称为强制换流。
必须指出,上述臂内换流和臂间换流方式也同样存在于容性负载,但臂内换流程序改为由VI→VD;臂间换流程序相应地为VD→VI,与上述感性负载过程相反,读者可自行分析。
根据图2-1d、e,逆变输出功率的瞬时值po为
po=uoio(2-11)由图可见,在0<ωt<ϕ1区间,po<0,说明在该区间电路工作于整流状态,负载端交流电能通过反并联二极管反馈到直流电源,于是在非纯阻性负载条件下,在一个工作周期内,逆变和整流工作状态交替出现,当ϕ1<π/2时,逆变状态的持续时间将较整流状态的长,负载端基波瞬时功率为
po1=uo1io1(2-12)按图2-1d所选的时间坐标,有
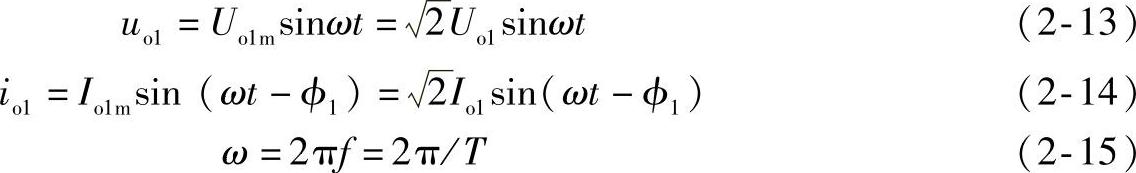
式中 Uo1、Io1——输出电压和电流的基波有效值。
将式(2-13)、式(2-14)代入式(2-12)有:
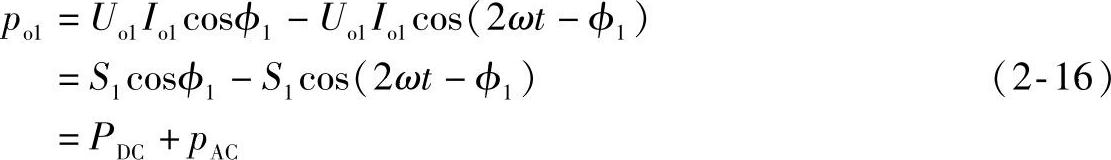
式中
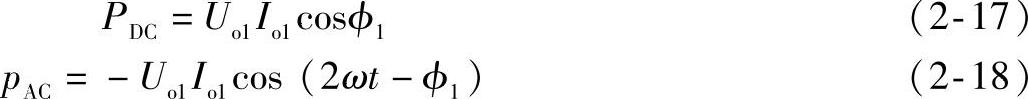
式(2-16)表明,基波功率瞬时值包含直流分量PDC和交流分量pAC,pAC以两倍基波频率规律变化,其平均值为零,因而基波平均功率为
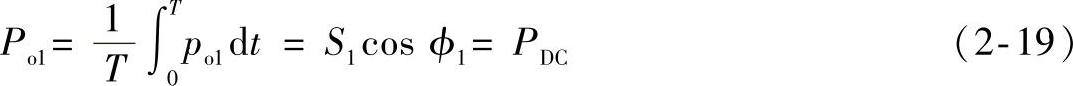
上式表明,逆变电路基波有功功率与平均功率相等。
全桥电流型逆变电路与电压型逆变电路呈对偶结构,如图2-3所示。输入由直流电流源Id构成,两个桥臂的开关器件用全控型开关器件和截止二极管串联构成单向开关VI1取代电压型逆变电路中并联续流二极管的双向开关;负载Z上承受电流方波,其电压值由负载自身决定。
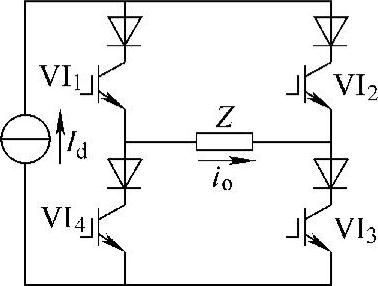
图2-3 全桥电流型逆变电路
值得注意的是,电流型逆变电路在换流过程中与电压型逆变器的臂内换流方式不同,采用的是臂间换流的方式,同一桥臂上的两个开关的驱动信号之间加入的也并非死区区间,而是重叠区间,目的是使被控对象——电流量能够安全换流。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






