根据被加工零件图样，按照已经确定的加工工艺路线和允许的编程误差，计算数控系统所需要输入的数据，称为数学处理。对零件图进行数学处理是编程前的主要准备工作之一，而且即便采用计算机进行自动编程，也经常需要先对工件的轮廓形状进行数学预处理，才能对有关几何元素进行定义。

图形的数学处理一般包括两个方面：一方面根据零件图给出的形状、尺寸和公差等直接通过数学方法（如三角、几何与解析几何法等）计算出编程时所需要的有关节点或基点坐标值，例如圆弧插补所需要的圆弧圆心相对起点的坐标增量I、J、K；另一方面是按照零件图给出的条件还不能直接计算出编程时所需要的节点坐标值，也不能按照零件图给出的条件直接进行工件轮廓几何元素的定义进行自动编程，那么就必须根据所采用的具体工艺方法、工艺装备等加工条件，对零件原图形及有关尺寸进行必要的数学预处理或改动，才可进行节点的坐标计算和进行正常的编程工作。

1.数值计算

编程原点设定后，可以采用以下两种方法求出具体数值：

（1）手工数值处理 利用代数、三角函数、几何与解析几何等数学工具、再加上计算器等求出具体数值。例如：图3-5中的各点坐标值计算如下：

A[-10×cos30，30+10×sin30]=A（-8.66，35）；

B[10×cos30，30+10×sin30]=B（8.66，35）；

C[30×cos30+10×cos30，-30×sin30+10×sin30]=C（34.641，-10）；

D[30×cos30，-30×sin30-10]=D（25.981，-25）；

E[-30×cos30，-30×sin30-10]=E（-25.981，-25）；

F[-30×cos30-10×cos30，-30×sin30+10×sin30]=F（-34.641，-10）。

（2）利用AutoCAD等CAD软件来求具体坐标数值 如图3-6所示，先画出图形来，再利用尺寸标注，把每一个节点相对于工件坐标系原点的坐标标注出来，就可以得到节点的具体坐标值。对于图3-5所示的零件，可以用AutoCAD软件来进行坐标值计算，根据图中的尺寸标注可以得出图中各点的坐标值如下：A（-8.66，35）；B（8.66，35）；C（34.641，-10）；D（25.981，-25）；E（-25.981，-25）；F（-34.641，-10）。

这里指的是用手工编程的方法进行数值计算，如果采用自动编程，就不必这样了。(www.daowen.com)

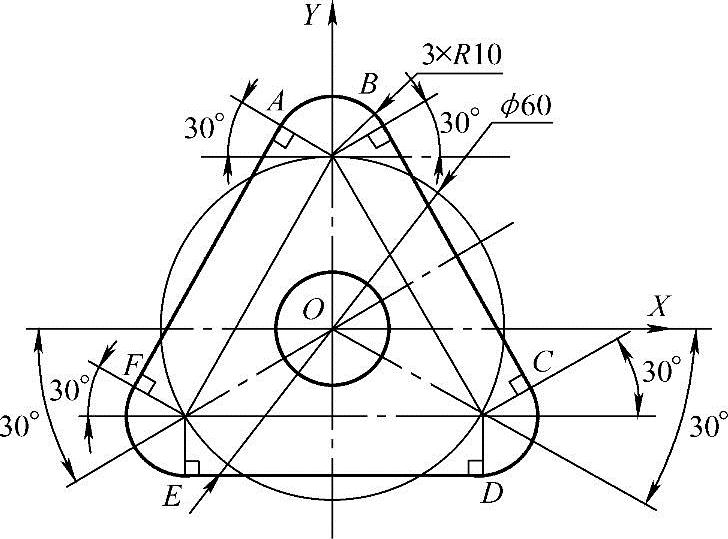
图3-5 利用代数、三角函数、几何与解析 几何等数学工具进行手工数值处理

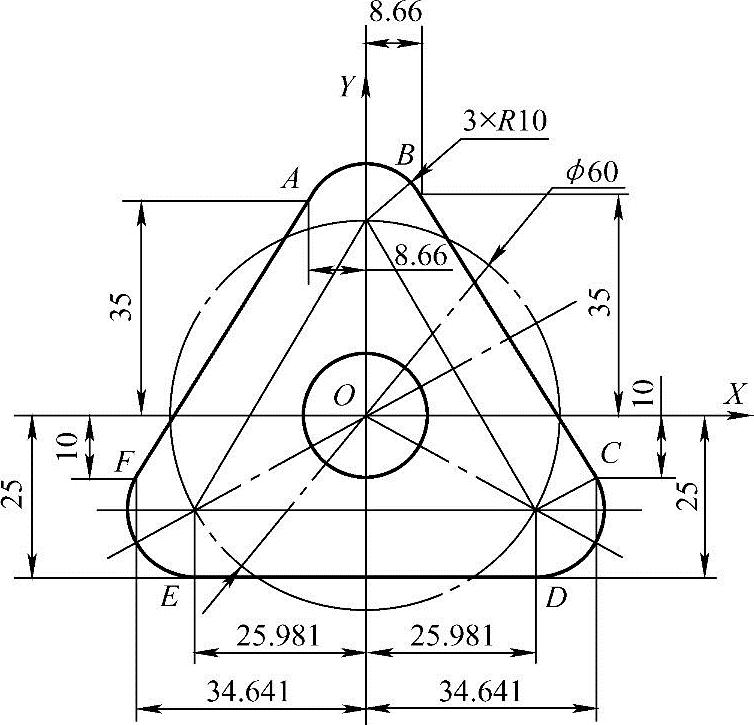
图3-6 利用AutoCAD软件来求具体坐标数值

2.基点与节点

（1）基点 零件的轮廓复杂多样，是由许多不同的几何元素所组成，例如直线、圆弧、二次曲线以及列表曲线等。各几何元素之间的连接点称为基点，例如两条直线的交点、直线与圆弧或圆弧与圆弧的交点或切点、圆弧与二次曲线的交点或切点等。目前，数控系统都具有直线、圆弧插补功能，对于由直线与直线或直线与圆弧构成的平面轮廓零件，数值计算比较简单，主要是计算出各基点坐标及圆弧的圆心点坐标。

（2）节点 当被加工零件轮廓形状是由直线段或圆弧之外的其他曲线构成，例如椭圆、双曲线、抛物线或用一系列坐标点表示的列表曲线，而数控系统又不具备该曲线的插补功能时，可用若干直线段或圆弧去逼近被加工曲线，逼近线段与被加工曲线的交点或切点称为节点，如图3-7所示。

在编程时，要计算出节点的坐标，并按节点划分程序段时，逼近线段的近似区间越大，则节点数目越少，相应的程序段数目也越少，但逼近线段的误差δ应小于或等于编程允许误差δ_允，即δ≤δ_允。考虑到工艺系统及计算误差的影响，δ_允一般取零件公差的1/5～1/10。为了编程方便，一般都采用直线段逼近已知的曲线，这种方法称为直线逼近或线性插补。节点拟合计算的难度及工作量都较大，故宜通过计算机完成，有时也可由人工计算完成。

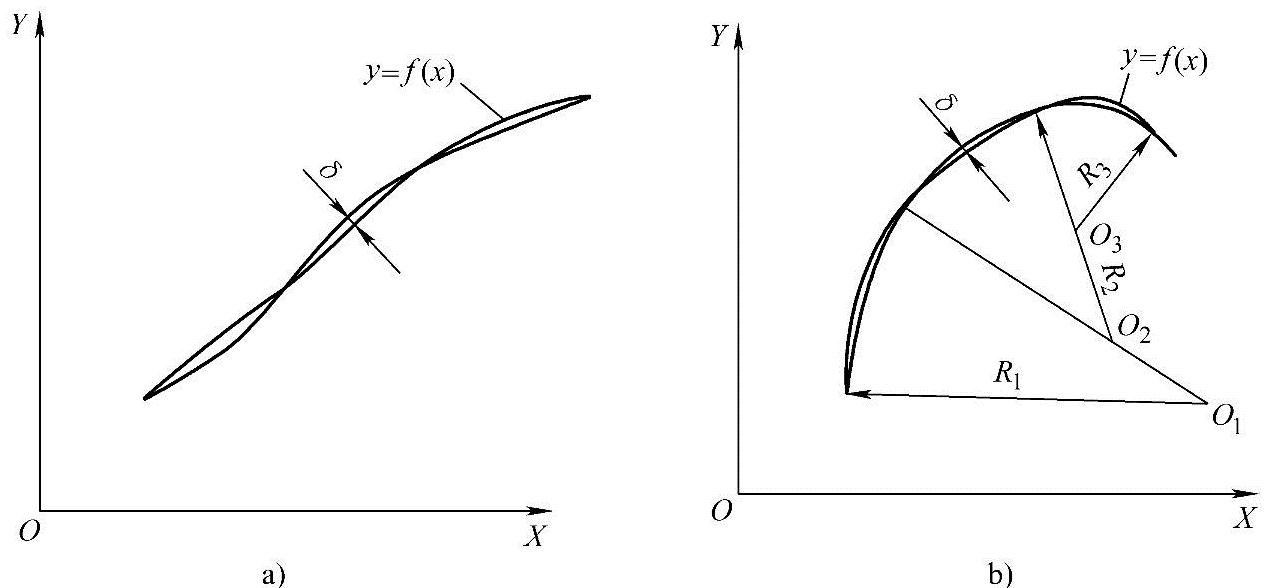
图3-7 非圆曲线的逼近

a）用直线段逼近非圆曲线 b）用圆弧段逼近非圆曲线