（1）模型建立。基于灌浆过程中渗流-应力耦合原理，分析研究区域内的工程地质与水文地质条件，概化水文地质模型，运用数值模拟方法建立耦合数学模型，其中研究区域为100m×100m，含水层为6m，泥岩为24m，粉砂岩为10m。导水断层切割顶板，导致顶板出水。地下工程建设中洞室断面为80m2（图8.2.1-1）。

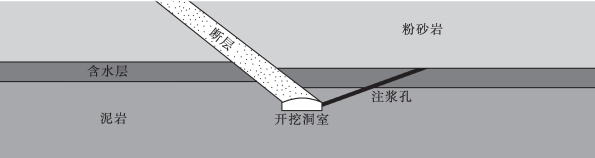
图8.2.1-1　模型建立

（2）网格划分。整个几何区域进行整体细化分网格，其中对灌浆周边围岩进行局域自定义超细划分网格。以增加模型收敛性和求解精度。网格属性：三角形单元总计6417个，边单元495个，端点单元24个。共有38096个计算自由度。最小单元质量为0.4433，平均单元质量0.9588，其中最大单元尺寸为2.22，最小单元尺寸为0.0075，曲率解析度为0.25，最大单元生长率为1.25。网格划分如图8.2.1-2所示。

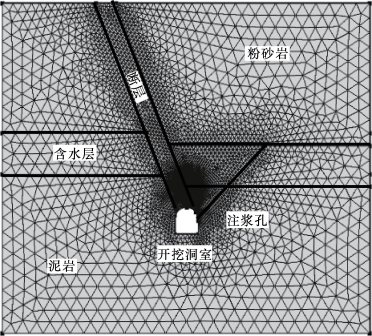
图8.2.1-2　网格划分

（3）参数选择。通过现场取样进行室内岩石力学实验，测得岩石物理力学特性。如弹性模量、泊松比及岩石比重。现场进行钻孔压水试验获得岩体渗透率，具体物理力学参数见表8.2.1-1。

表8.2.1-1　地层物理力学参数

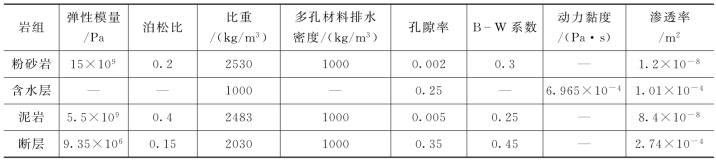
（4）初始条件及边界条件。初始孔隙水压力为1MPa，含水层为承压水，水压为3MPa，其中断层切割含水层导致顶板涌水，涌水处设置压力为零（与大气相通），对于含水层与粉砂岩、泥岩之间设置透水层边界，并且模型周边为不流动流体，考虑流体自重因素影响。对于应力边界，模型周边为固定，不存在位移，由于灌浆过程中围岩变形均作用在开挖断面周边。体积力设置为岩体自重，不考虑地层运动引起构造应力重分布。

灌浆压力加载与灌浆孔端部，其中模拟灌浆时间为4h，围岩变形监测为20h。对选取的20号、15号、16号、11号点分别进行围岩变形监测。

（5）岩体破坏准则。灌浆过程中围岩发生弹塑性变形，甚至发生破坏，其中工程岩体在灌浆荷载作用下表现出来的复杂破坏，归结为拉伸和剪切破坏两种机制；将影响岩体强度的复杂因素，集中包含在准则引用的两个经验参数m（岩石软硬程度）、s（岩体破坏程度）之中。采用Hoek-Brown经验强度准则评判灌浆过程中围岩变形及破坏情况。即为Hoek-Brown强度准则，也称为狭义Hoek-Brown强度准则。其表达式为

(www.daowen.com)

式中：σ1、σ3分别为岩体破坏时的最大、最小主应力，MPa；σc为岩体块单轴抗压强度，MPa，由单轴压力试验和点荷载试验测定；m、s均为经验参数，m反映岩石的软硬程度，其取值范围在0.0000001～25之间，对严重扰动岩体取0.0000001；对完整的坚硬岩体取25；s反映岩体破碎程度，其取值范围在0～1之间，对破碎岩体取0，完整岩体取1。

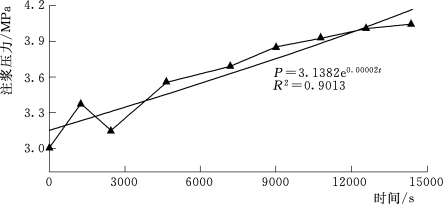
图8.2.1-3　灌浆压力4MPa变化曲线

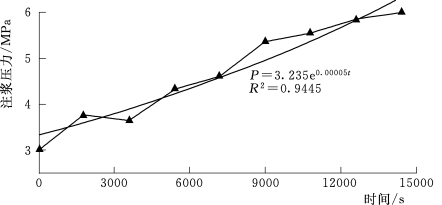
图8.2.1-4　灌浆压力6MPa变化曲线

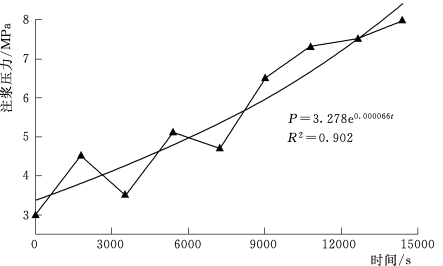
图8.2.1-5　灌浆压力8 MPa变化曲线

基于地下水渗流理论与应力变形相互影响、相互作用，以有限元为基础，采用COMSOL数值模拟方法，通过偏微分方程组进行流固耦合研究灌浆压力下围岩变形规律。其中含水层水压为3MPa，灌浆材料为水泥浆液，水灰比为1∶1，灌浆终压分别为4MPa、6MPa、8MPa，依据大量的现场实验数据，选取典型工程，进行灌浆压力-时间曲线（P-t曲线），如图8.2.1-3～图8.2.1-5所示。围岩变形影响因素具有多因素多水平特点，选用正交试验法进行研究。对灌浆终压、围岩等级、孔口管长度三个可控因素，进行三因素三位级研究。划分九个不同工况研究各因素条件下对围岩变形影响（表8.2.1-2）。隧道断面选取四个关键点进行围岩变形监测，分别为20号、11号、15号、16号（图8.2.1-6）。

表8.2.1-2　围岩变形正交试验

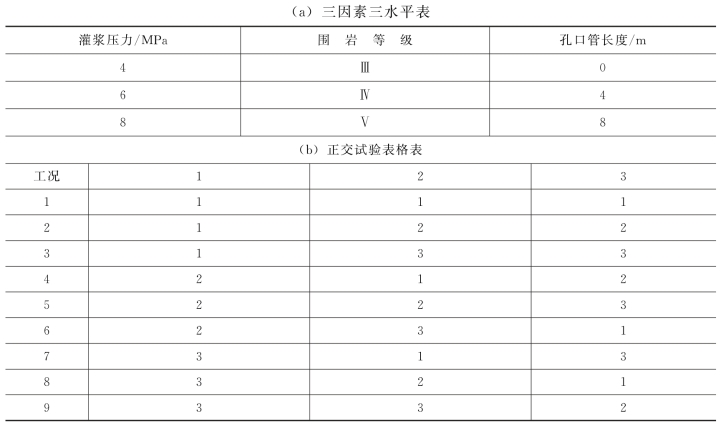
注　正交试验中任两列不存在交互作用。

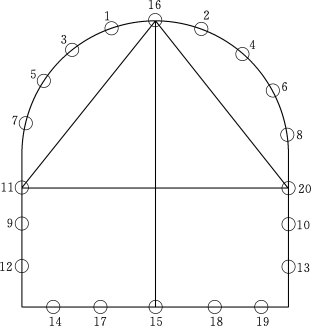
图8.2.1-6　围岩变形监测点示意图