单液水泥浆液是灌浆工程中应用最为广泛的浆材，能够满足大多数静水灌浆工况的要求；而在动水灌浆工程中，水泥浆液存在着易跑浆、难留存等缺陷，单液水泥浆扩散及封堵规律认识不足，亟待进行深入理论研究。

大量灌浆模型试验研究表明，动水条件下单液水泥浆扩散遵循一个重要规律，即平面裂隙动水条件下，不同类型和不同参数的水泥单液浆进入稳定扩散状态后，在不受外力干扰或灌浆参数保持不变的条件下，其扩散区域是稳定不变的，扩散迹线呈现标准的U形，称之为U形扩散规律，如图3.1.1-1所示。

图3.1.1-1　动水条件下单液水泥浆稳定扩散状态（山东大学）

为便于研究和准确刻画浆液稳定扩散形态，建立了以灌浆孔圆心为坐标原点、动水流场方向为x轴正方向、裂隙平面内垂直于x轴为y轴的二维笛卡尔坐标系（图3.1.1-2）。定义浆液稳定扩散状态中，x轴上最小坐标值为浆液逆水扩散距离，用符号N表示，定义y轴方向的稳定宽度为扩散开度，用符号L表示。显然，L和N决定着浆液的扩散范围，同时，L和N也是灌浆参数和流场参数的函数。通过扩散形态轮廓线描绘，总结出平面裂隙动水条件下浆液扩散规律如下：

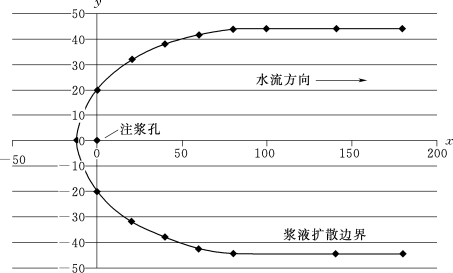
图3.1.1-2　浆液动水扩散形态素描图（单位：cm）

1）浆液扩散形态固定，呈标准U形扩散，并且满足动水灌浆扩散公式（3.1.1-1）；

2）浆液扩散范围只取决于N和L，L和N由灌浆参数和相关流场参数决定；

3）当x＞L-N时，浆液的扩散为等开度扩散；

在以灌浆孔圆心为坐标原点的平面裂隙浆液扩散模型中（图3.1.1-3），有如下关系式：

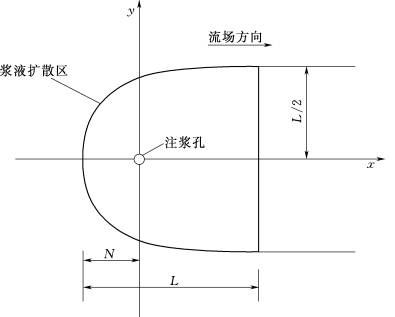
图3.1.1-3　浆液U形扩散模型

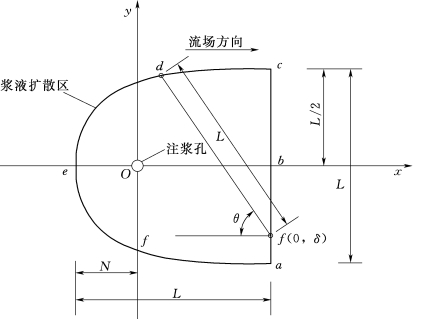
当-N＜x＜L-N时，浆液的扩散形状较为特殊，通过对多组扩散试验的稳定扩散轮廓素描图进行研究，找出了该区段的扩散规律，并研究了一个可以准确刻画该段浆液扩散规律的方法，建立了动水灌浆浆液扩散数学模型，如图3.1.1-4所示。模型中，在x∈[-N，L-N]取值范围内，浆液在y轴方向的扩散宽度随x坐标的增大而增加，同时，在x=L-N处达到最大值，即扩散开度L。

我们注意到，在扩散模型中，ac段和be段长度均为L，在e点，

(www.daowen.com)

图3.1.1-4　动水灌浆浆液扩散数学模型

扩散边界的切线与y轴平行，同时在a、c两点，其切线与x轴平行。

为了准确刻画曲线aec的轨迹，假定有一根长度为L的杆df，其中f端沿线段ac由a点向c点运动，则f点的坐标定义为（L-N，δ），与此同时，d点沿着弧线aec做逆时针转动，当f端由a点运动至b点时，运动距离为L/2，同时d端则由c点转动至e点，转动角度为π/2。定义d点坐标为（x，y），则有如下关系：

式（3.1.1-2）和式（3.1.1-3）中的θ和δ均为计算模型中构建出来的两个参数，定义θ在x轴上方时为正，在x轴下方时为负，由此可以得到θ的取值范围为[-π/2，π/2]，δ的取值范围为[-L/2，L/2]。同时由浆液扩散数学模型可知，δ与θ的边界为：δ=-L/2，θ=π/2；δ=L/2，θ=-π/2；用几何测量的方法对试验扩散边界（L=83cm）进行统计记录，θ和δ试验量测值见表3.1.1-1。

表3.1.1-1　θ和δ试验量测值

根据试验结论，绘制θ和δ的关系对应曲线（图3.1.1-5），得到δ=f（θ）是一个非线性反对称奇函数。并且其关系满足正弦定律。

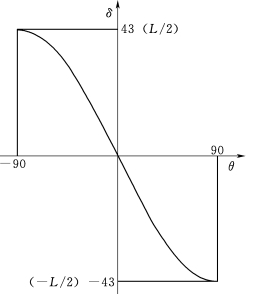
图3.1.1-5　θ和δ关系对应曲线

将式（3.1.1-4）分别代入式（3.1.1-2）和式（3.1.1-3）中，联立便可得到浆液的扩散公式如下：

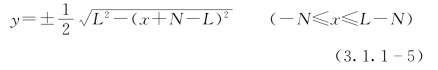
式（3.1.1-5）联立式（3.1.1-1）可以得到浆液扩散区域的计算公式：

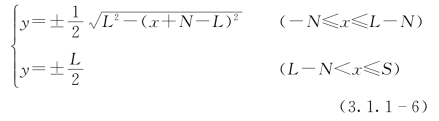
式中：L为扩散开度；N为逆水扩散距离；S为顺水的扩散距离。