【例7-7】死区非线性的输入和输出特性实例。在Simulink中，利用幅值为1的正弦信号直接作用于限幅为0．5的死区非线性模块，试求其输出，并与输入信号进行比较。

解:具体步骤如下:

(1)在Simulink的library窗口中选择【File】｜　【New】命令，建立一个新的Simulink工作平台。

(2)分别将信号源库、输出方式库、信号路线和非线性环节库中的Sine、Scope、Mux和Dead Zone各功能模块拖至工作平台。

(3)按系统要求将各模块加以连接，如图7-25所示，并对模块进行参数设置，如设置死区非线性模块的“Start of dead zone”为－0．5，“End of dead zone”为0．5；

(4)执行仿真，结果如图7-26所示。

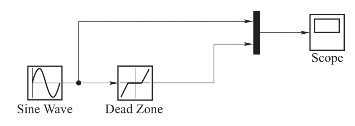
图7-25　Simulink仿真模型

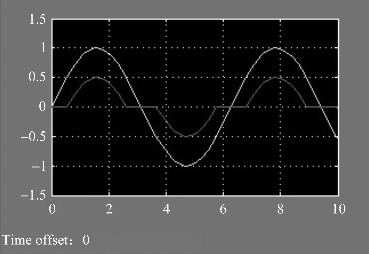
图7-26　仿真结果

【例7-8】设系统如图7-27所示，试分别用描述函数分析法和相平面分析法判断系统的稳定性，并画出系统c(0)＝0、c(0)＝3的相轨迹和相应的时间响应曲线。

解:(1)描述函数分析法。非线性环节的描述函数为

在复平面内分别绘制线性环节的G(jω)曲线和负倒数描述函数－1/N(A)曲线，利用奈氏判据，若G(jω)曲线不包围－1/N(A)曲线，则非线性系统是稳定的；反之，非线性系统不稳定。

图7-27　饱和非线性系统

MATLAB程序如下:

在MATLAB中运行上述M文件，作出G(jω)曲线和负倒数描述函数－1/N(A)曲线，如图7－28所示。图中G(jω)曲线不包围－1/N(A)曲线，根据非线性稳定判据，该非线性系统稳定。

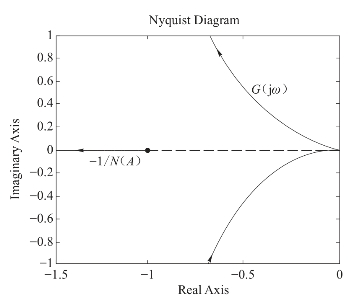
图7-28　描述函数分析法

(2)相平面分析法。描述该系统的微分方程为在相平面上绘制c与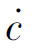的关系曲线，需要首先确定上述系统微分方程在一定初始条件下的解，完成这一求解步骤一般非常困难，借助于MATLAB软件，求解过程可以大大简化。通过分析相轨迹的运动形式，直观地判断非线性系统的稳定性。

MATLAB程序如下:

图7-29　相轨迹

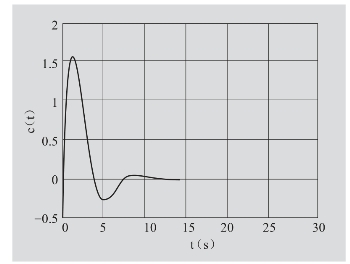
图7-30　时间响应曲线(www.daowen.com)

在MATLAB中运行上述M文件后，得系统相轨迹和相应的时间响应曲线，分别如图7-29和图7-30所示。由图可见，系统振荡收敛。系统的奇点为稳定焦点。

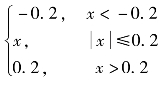【例7-9】已知一个非线性系统如图7-31所示，输入为零初始条件的线性环节G(s)＝，其中，T＝1，K＝4，N为理想饱和非线性y(x)＝，系统的初始状态为0，要求:

(1)在e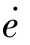－平面上画出相轨迹；

(2)给出e(t)、c(t)的时间响应波形。

解:取状态变量e(t)和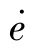(t)。

首先利用Simulink搭建模型，如图7-32所示。

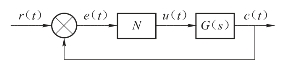
图7-31　例7-9图

图7-32　Simulink仿真模型

要在XY Graph上绘出相轨迹，关键是得到e、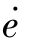的信号。e直接取自比较器的输出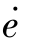，可在e后面加一阶微分环节实现，然后把两个信号接到XY Graph便可画出相轨迹。

取“Fixed Step”和“Solver”为0．05，“Stop time”为40。

运行Simulink，XY Graph绘出的相轨迹如图7-33所示。

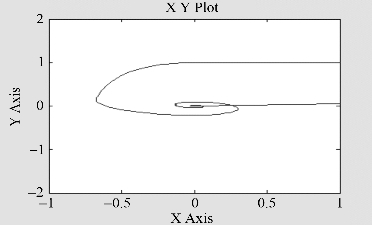
图7-33　仿真结果

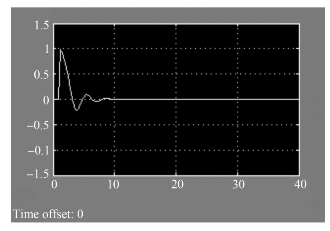
图7-34　e(t)的时间响应波形

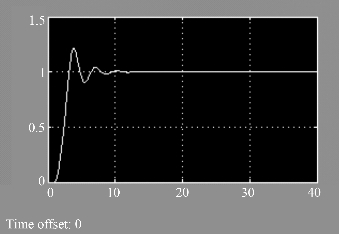
图7-35　c(t)的时间响应波形

双击比较环节连接的单踪示波器，会看到e(t)的时间响应波形，如图7-34所示；双击系统输出连接的单踪示波器，会看到c(t)的时间响应波形，如图7-35所示。

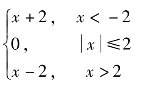【例7-10】设非线性控制系统如图7-36所示，其中，G1(s)＝5，G2(s)＝　，G3(s)＝，非线性环节为死区非线性y(x)＝，使用Simulink分析系统单位阶跃响应，并绘制响应曲线。

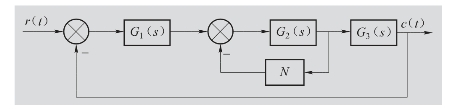
图7-36　例7-10图

解:系统仿真模型如图7-37所示，系统阶跃响应曲线如图7-38所示。

图7-37　Simulink模型

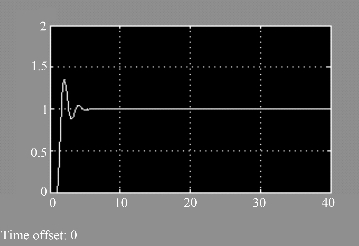
图7-38　仿真结果