非线性特性在进行谐波线性化之后，仿照线性系统幅相频率特性的定义，可建立非线性特性的等效幅相特性，即描述函数。

含有本质非线性环节的控制系统其结构图一般如图7-21所示。

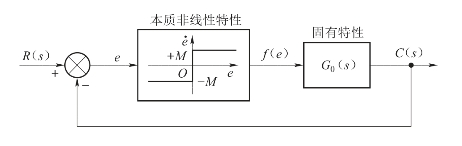
图7-21　含有本质非线性环节的控制系统

图7-21中，G0(s)为控制系统的固有特性，其频率特性为G0(jω)。一般情况下，G0(jω)具有低通特性，也就是说，信号中的高频分量受到不同程度的衰减，可以近似认为高频分量不能传递到输出端。那么非线性环节对于输入信号的基本频率分量的传递能力就可以提供系统关于自持振荡的基本信息。

因此，描述函数定义如下:

设非线性环节的输入－输出关系为

y＝f(x)

(7-29)

当非线性环节的输入信号为正弦信号

x(t)＝Xsinωt

(7-30)

式中，X是正弦信号的幅值，ω是正弦信号的频率。则输出信号y(t)为周期非正弦信号，可以展开为傅氏级数为

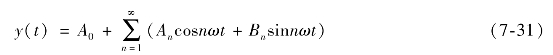
式中，A0为直流分量。如果y(t)为奇函数，则有(www.daowen.com)

A0＝0

(7-32)

An、Bn为傅里叶系数，则正、余弦谐波分量的幅值分别为

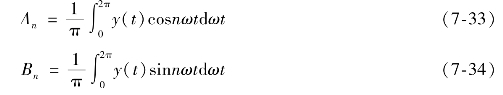
n等于1时的一次谐波分量也称为基波分量。在傅氏级数中谐波阶次n越大，谐波分量频率越高，系数An、Bn越小，若此时系统又满足G0(jω)具有低通特性，则高次谐波分量又进一步充分衰减，故可近似认为非线性环节的稳态输出只含有基波分量，于是式(7-31)可简化为

式中，

仿照线性系统中频率特性的定义，把非线性元件稳态输出的基波分量与输入正弦信号的复数比定义为非线性元件的等效幅相特性，即描述函数，用N(A)来表示，即

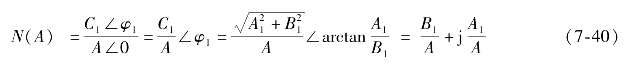
－1/N(A)称为描述函数的负倒数特性。

由非线性环节的描述函数定义可以看出:

(1)通过描述函数可以将一个非线性元件近似看作一个线性元件，非线性系统的描述函数类似于线性系统的频率特性。

(2)描述函数表示的是非线性元件对基波正弦量的传递能力，略去了高频分量的传递，因此不同于线性系统的频率特性。

线性系统的频率特性反映的是在正弦信号作用下，系统稳态输出中与输入同频率的分量的幅值和相位相对于输入信号的变化；而非线性环节的描述函数则反映的是非线性系统正弦响应中一次谐波分量的幅值和相位相对于输入信号的变化。后者忽略高次谐波分量，仅考虑基波分量，非线性环节的描述函数表示为复数增益的放大器。