作出系统的相平面图，就可以利用相平面图进行系统分析了。尤其是对于那些具有间断特性的非线性系统，利用相平面图进行分析更为方便，如继电特性、死区特性等。

相平面图分析的一般步骤如下:

首先需要作出系统在相平面上运动的相轨迹。对于上述具有间断特性的非线性系统，其输入作用一般表示为数学上的分区作用，因此，在相平面上的相轨迹也是分区作出的。

其次，分析系统的稳定性。由分区穿越的各段构成的相轨迹最终是收敛还是发散，可知非线性系统相轨迹的敛散性，也就确定了该非线性系统的稳定性。

再次，分析系统是否具有极限环。极限环是非线性系统独有的特征，因此，通过极限环是否存在、是否是稳定极限环、极限环运动区域的大小等，也就确定了该非线性系统有关自持振荡的主要信息。

最后，可以参考线性系统的性能指标来考虑该非线性系统的调节时间与超调量等。

在相平面分析时，通常将输入作用下系统的运动化为系统的自由运动来考虑。这样，x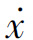－相平面就化为e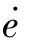－相平面。一般情况下，参考平衡点在坐标变换下转移到原点。系统误差的各阶导数为

因此有

将上述各式代入原方程即可得到以误差e(t)为运动变量的微分方程了，从而对应的平面为e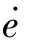－　平面。

【例7-5】非线性系统的描述方程为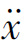＋0．5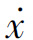＝－2x－x2，采用相平面分析法分析该系统奇点的稳定性。

解:由奇点的定义，令

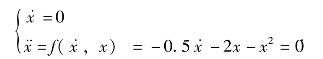
由此求得系统的奇点有两个，分别为x1＝(0，0)和x2＝(－2，0)。

对于奇点x1，在其邻域进行泰勒级数展开，得到系统在x1邻域附近的线性化方程为

求解该方程得到系统的特征根为λ1，2＝－0．25±j1．39，由此可见，奇点x1＝(0，0)是稳定焦点。

类似地，得到系统在x2邻域附近的线性化方程为

令y＝x＋2，代入上式，得到(www.daowen.com)

该方程的根分别为1．19和－1．69。由此可见，奇点x2＝(－2，0)是鞍点。

从图7-18所示的非线性系统相轨迹可看出，进入鞍点(－2．0)的两条相轨迹还是分隔线，它们将相平面划分成两个不同的区域。若系统初始状态位于图中的阴影区城内，则相轨迹将收敛于坐标原点，系统是稳定的:反之，若系统初始状态位于图中的阴影区域外，则相轨迹将趋于无穷远，系统是不稳定的。

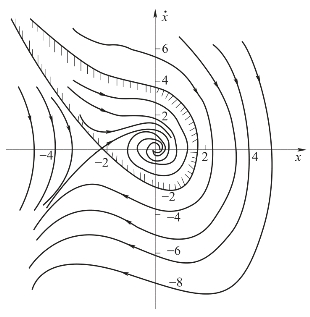
图7-18　例7-5中非线性系统的相轨迹

【例7-6】带有饱和特性的非线性系统如图7-19所示，试用相平面分析法做系统分析。

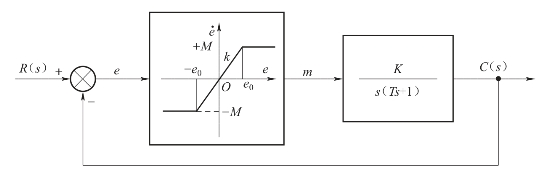
图7-19　带有饱和特性的非线性控制系统

解:系统线性部分运动方程为

非线性部分为

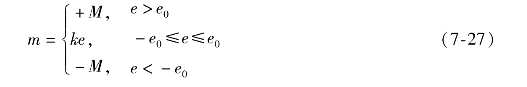
此处m为饱和特性的输出，代入线性部分运动方程即得到三个运动方程为

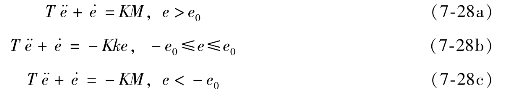
这三个运动方程分别表达了系统在三个分区中的运动特性。

式(7-28a)、式(7-28c)的相轨迹与继电特性的相轨迹相同，但是由饱和点所决定，切换位置提前，式(7-28b)的相轨迹为线性系统的运动特性。由于式(7-28b)的奇点性质为稳定焦点，所以最后一次进入Ⅱ区后，相轨迹不再进入其他工作区，在Ⅱ区内经有限次振荡后，最终收敛于原点，如图7-20所示。

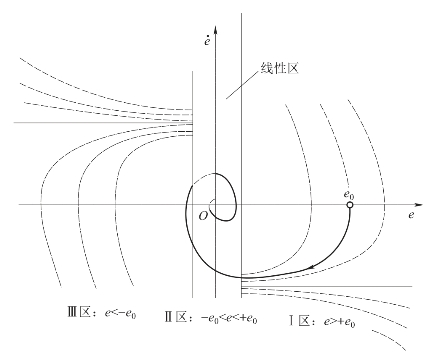
图7-20　饱和非线性系统的相轨迹

从饱和特性的相平面分析可以看到:

(1)如果系统的固有部分具有良好的阻尼特性，系统最后进入Ⅱ区后，在超调量、调节时间、振荡次数等方面均呈现良好的动态特性，而且不产生自持振荡。

(2)饱和点的大小可以决定分区切换次数的多少。饱和点的值大，则线性工作区大，分区切换次数少，非线性振荡次数少，饱和非线性对系统的影响小；饱和点的值小，则线性工作范围小，分区切换次数增加，非线性振荡次数增多，饱和非线性对系统的影响就不可忽视。