系统相轨迹在相平面上的运动有一定规律，了解相轨迹的运动特性可以使得相平面作图简化。

1.相轨迹的运动方向

在上半相平面，因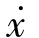＞0，故上半平面相轨迹的走向是沿着x的增加方向，即由左至右。在下半相平面，因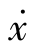＜0，故下半平面相轨迹的走向是沿着x的减小方向，即由右至左。

在实轴上，由于有速度变量　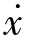＝0，由相轨迹斜率方程

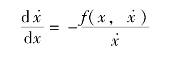
可得相轨迹斜率为正负无穷。

上述相轨迹的运动方向可归结为:

(1)上半平面的相轨迹右行；

(2)下半平面的相轨迹左行；

(3)穿过实轴的相轨迹斜率为±∞。

相轨迹的基本运动方向如图7-13所示。

2.相轨迹的对称性

某些系统的相轨迹在相平面上满足某种对称条件，相轨迹的对称性可以由对称点上相轨迹斜率来判断。因此依据对称条件，相轨迹曲线可以对称画出。

(1)x轴的对称条件(上下对称)。

图7-13　相轨迹的运动方向

若相轨迹关于x轴对称，则在对称点(x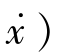，和(x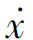，　－)上，相轨迹斜率大小相等，符号相反。

因为相轨迹斜率方程为

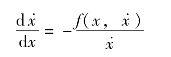
所以当满足

时，相轨迹关于x轴对称。

(2)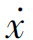轴的对称条件(左右对称)。

若相轨迹关于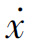轴对称，则在对称点(x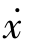，　)和(－x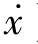，)上，相轨迹斜率大小相等，符号相反。

即当满足

时，相轨迹关于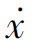轴对称。

(3)原点对称条件(中心对称)。

若相轨迹关于原点对称，则在对称点(x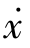，)和(－x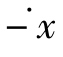，)上，相轨迹斜率相同。

即当满足

时，相轨迹是关于原点对称的。

相轨迹的对称如图7-14所示。

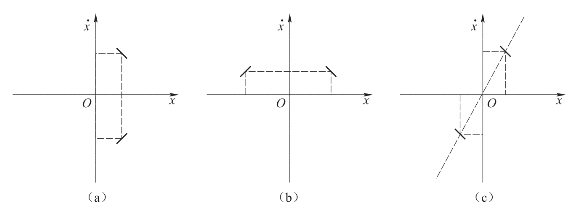
图7-14　相轨迹的对称

(a)x轴对称；(b)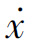轴对称；(c)原点对称

3．相轨迹的时间信息

相轨迹反映了系统的运动情况。相轨迹上任一点代表了系统在某一时刻的状态，而在相平面图上，时间变量t为隐含变量。因此，不能直接从相平面图上得到相变量x、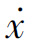与时间变量t的直接关系。(www.daowen.com)

当需要从相平面图上得到相变量与时间的函数关系曲线x(t)、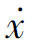(t)时，可以采用增量法逐步求解得到。

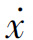由于，当dx、dt分别取增量Δx、Δt时，就是增量段的平均速度，所以由增量式可以写出

增量Δx与平均速度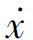可以从相平面图上读到，因此也就得到了对应增量段上的时间信息。将增量信息Δt、Δx、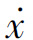表示在x－t平面或者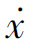－t平面上，便可以得到相变量与时间的函数关系曲线x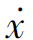(t)、(t)。

图7-15(a)所示即为相平面图上时间信息的几何说明，图7-15(b)为根据时间信息得到的时间关系曲线x(t)。

图7-15　相平面图上的时间信息

(a)相平面图的增量；(b)时间关系曲线

4．相轨迹的奇点

用相平面分析法分析系统的要点之一是确定奇点及奇点的类型，从而可以确定系统相轨迹在奇点附近的分布，判断系统的工作状态。

二阶系统为

相轨迹的斜率方程为

将相平面上同时满足

的点定义为相轨迹的奇点。

奇点是相平面上的一类特殊点。所谓奇点，指的是相平面上满足d/dx＝0，dx/dt＝0的点。显然，在奇点处，相变量的各阶导数均为零，这表示系统处于平衡状态，因此奇点也称为平衡点。

在奇点处，相轨迹斜率d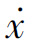/dt＝为不定值，也就意味着从奇点处可以引出无穷多条相轨迹。

以二阶线性定长系统为例，

方程的特征根为

显然，该系统的奇点是相平面的奇点。由于奇点的特性和奇点附近相轨迹的行为主要取决于系统的特征根λ1、λ2在s平面上的分布情况，因此根据线性化方程特征根λ1、λ2在s平面上的分布情况，奇点可分为稳定节点、不稳定节点、稳定焦点、不稳定焦点、鞍点和中心点等6类，如表7-1所示。

表7-1　二阶线性定常系统奇点的性质

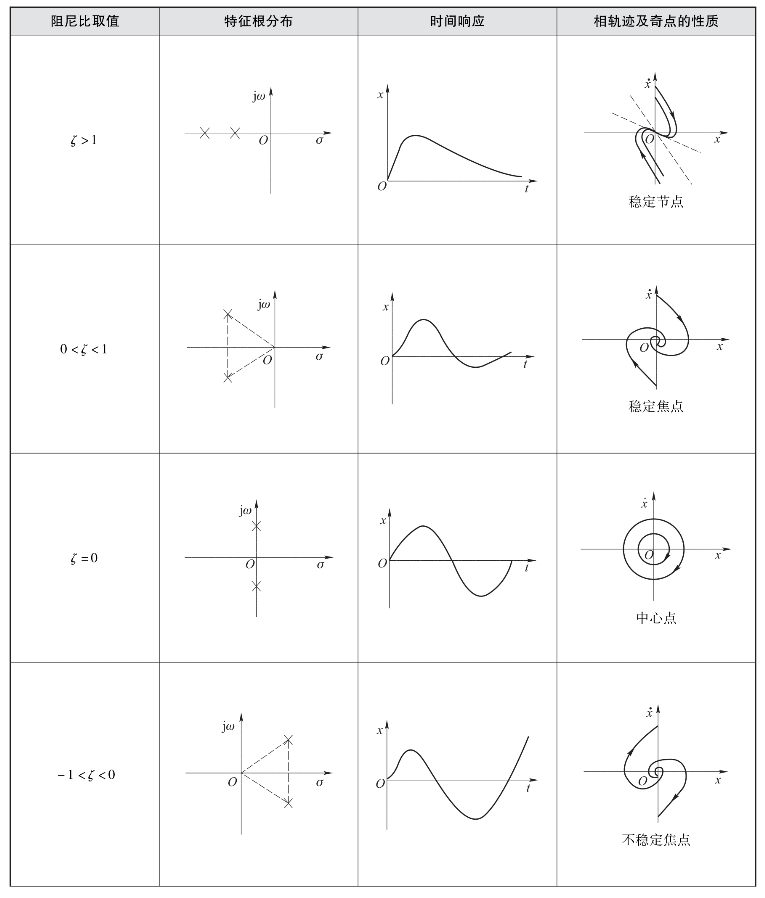
续表

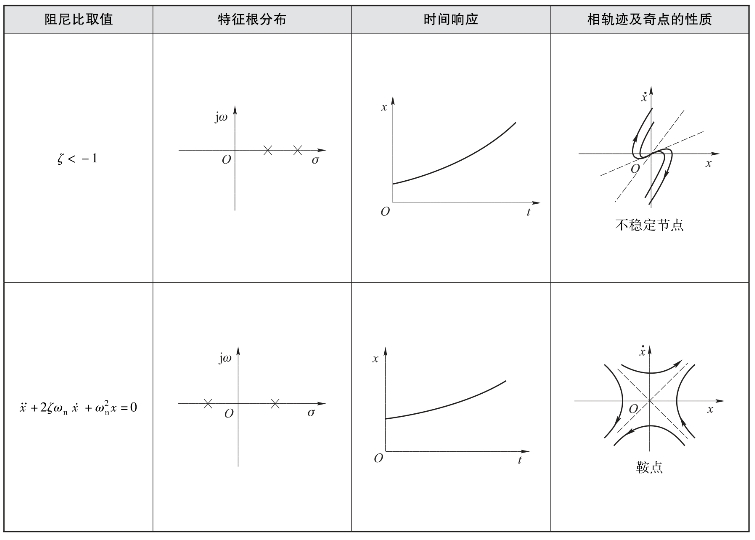
5．极限环

若非线性系统的相轨迹在相平面图上表现为一个孤立的封闭曲线，所有附近的相轨迹都渐近地趋向或离开这个封闭的曲线，则这个封闭的相轨迹称为极限环。

非线性系统中的自持振荡状态在相平面图上的表现就是一个极限环，在相平面上成为闭合的相轨迹，如图7-16所示。

图7-16　几种极限环的自持振荡情况

在极限环邻域，相轨迹的运动如果趋向于极限环而形成自持振荡，则称为稳定极限环，否则称为不稳定极限环，如图7-17所示。

一般情况下，控制系统中不希望有极限环产生，即使不能做到把它完全消除时，也要设法将其振荡的幅值限制在工程允许的范围之内。

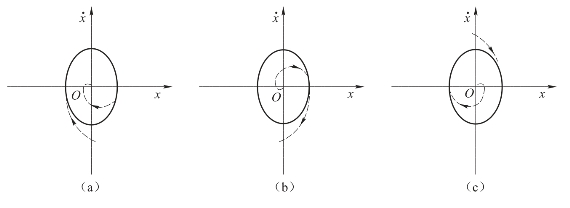
图7-17　极限环稳定与不稳定

(a)原点稳定；(b)不稳定极限环；(c)稳定极限环