由于非线性特性的存在，非线性系统与线性系统相比，具有下述的主要特征。

(1)叠加原理不适用于非线性控制系统，即几个输入信号作用于非线性控制系统所引起的输出，不再等于每一个输入信号所引起的输出之和。

(2)对于线性控制系统，当系统处于稳定的临界状态时，会产生等幅振荡，但其振幅随初始条件的不同而不同，而且只要系统参数有微小变化，就会造成虚轴上的极点的移动，等幅振荡就会消失。而在非线性控制系统中，常常产生自激振荡现象。所谓自激振荡是指在没有外界周期变化信号的作用时，系统内产生的具有固定周期和幅值的稳定振荡过程，简称自振。这是非线性系统的又一个重要特征。

(3)在线性控制系统中，当输入为正弦信号时，其输出为同频率的正弦信号，可以用频率特性来描述。但在非线性系统中，输入是正弦信号时，输出通常是非正弦周期函数，甚至还会出现谐波振荡或跳跃谐振等现象。

(4)对于线性控制系统，其稳定性与输入信号的大小及初始条件无关，只取决于系统的结构和参数。而对于非线性控制系统，其稳定性不仅与系统的结构和参数有关，与输入信号大小和初始条件也有关。

例如，考虑下述非线性一阶系统

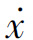＝x2－x

令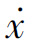＝0，可知该系统存在两个平衡状态x＝0和x＝1。为了分析各个平衡状态的稳定性，需要求解上述方程式。设t＝0时，系统的初始状态为x0，可得

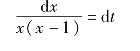(www.daowen.com)

积分得到

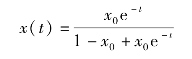
相应的时间响应随初始条件而变。当x0＞1，t＜ln时，x(t)随t增大，x(t)递增；t＝ln时，x(t)为无穷大；当x0＜1时，x(t)递减并趋于0。不同初始条件下时间响应曲线如图7-7所示。

考虑上述平衡状态受小扰动的影响，故平衡状态x＝1是不稳定的，因为稍有偏离，系统就不能恢复至原平衡状态；而平衡状态x＝0在一定范围的扰动下(x＜1)是稳定的。

由上例可知，非线性系统可能存在多个平衡状态，各平衡状态可能是稳定的，也可能是不稳定的。初始条件不同，自由运动的稳定性亦不同。更重要的是，平衡状态的稳定性不仅与系统结构和参数有关，而且与系统的初始条件有直接关系。

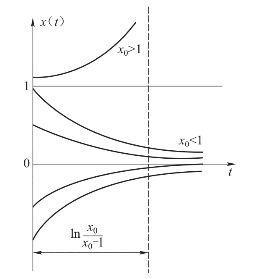
图7-7　非线性一阶系统的时间响应曲线

由此可见，非线性系统要比线性系统复杂很多，可能存在多种运动状态。上述现象均不能用线性理论进行解释或分析，必须应用非线性理论来研究。