利用MATLAB对控制系统进行校正时，可以免去手工计算相关的性能指标，直接利用计算机求解，特别是幅值裕度和相位穿越频率可以通过调用函数精确求出；并且通过仿真曲线判断校正后的系统是否满足设计要求。

MATLAB中绘制波德图及阶跃响应曲线的常用命令及函数在系统分析中已经有所介绍，本节将通过例6-7、例6-8介绍MATLAB在系统校正中的应用。

【例6-7】某单位负反馈系统的开环传递函数为G0(s)＝，要求系统达到性能指标为:最大超调量σp%≤5%；调节时间ts≤1 s；已知串联校正装置的传递函数为Gc(s)＝；校正后的系统的开环传递函数为Gk(s)＝　。试利用MATLAB比较系统校正前后的性能，并求出开环频域指标和单位阶跃曲线。

解:(1)求校正前系统的开环频域指标和单位阶跃曲线，MATLAB程序如下:

求得校正前开环频域指标为:

校正前，系统的幅值裕量为无穷大，相位裕量为11．4°；相位穿越频率为无穷大，幅值穿越频率为0．99 rad/s。系统的开环波德图如图6-43所示，闭环系统的单位阶跃响应曲线如图6-44所示，通过鼠标点击曲线最大峰值，则可得到最大超调量σp%＝73%，调节时间ts＝44．1 s。这与控制性能的要求相比相去甚远。

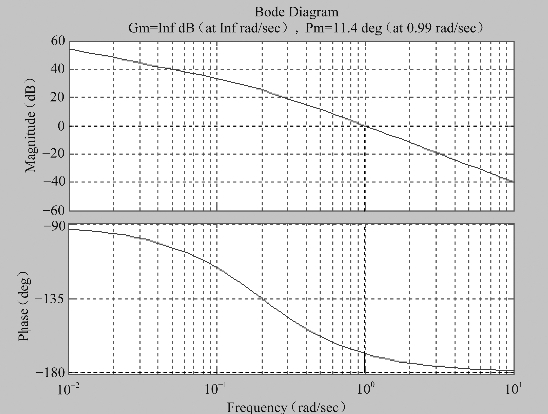
图6-43　系统校正前开环波德图

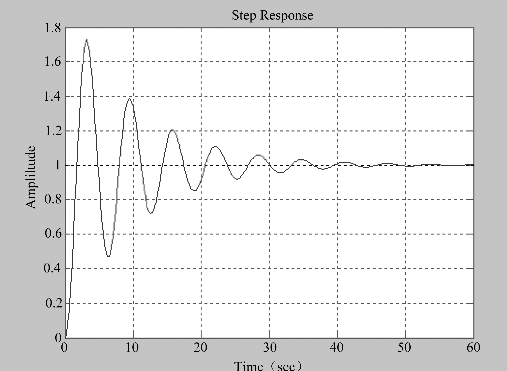
图6-44　系统校正前单位阶跃响应曲线

(2)通过串联校正后，得到的传递函数为Gk(s)＝；只需要在MATLAB的程序中修改数值，即可得到校正后系统的开环频域特性和单位阶跃响应曲线。修改后的MATLAB程序如下

求得校正后开环频域指标为:

图6-45和图6-46为校正后系统的开环波德图及闭环阶跃响应曲线。从图中可以看到，校正后系统的相位裕度为65．5°，幅值穿越频率为9．1 rad/s，单位阶跃响应的最大超调量σp%＝4%，调节时间ts＝0．5 s左右，满足了本题的要求。

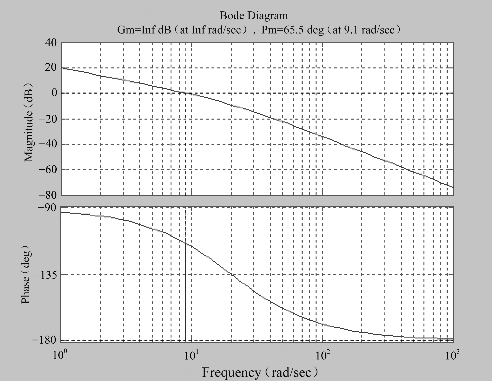
图6-45　系统校正后开环波德图

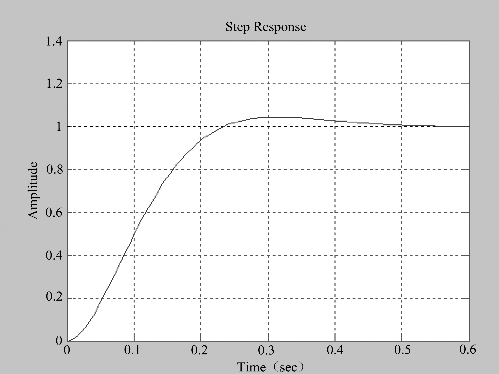
图6-46　系统校正后单位阶跃响应曲线

【例6-8】已知单位反馈开环传递函数为Gk(s)＝，试设计系统的相位超前校正装置，使系统:

(1)在斜坡信号r(t)＝t作用下，系统的稳态误差ess≤0．001v0(v0为斜坡函数系数)。

(2)校正系统的相位稳定裕度γ满足43°＜γ＜48°。

解:(1)求K0。

在斜坡信号作用下，系统的稳态误差为

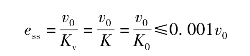
可得Kv＝K＝K0≥1 000 s－1，取K0＝1 000 s－1，则被控对象的传递函数为

(www.daowen.com)

(2)作原系统的波德图与阶跃响应曲线，如图6-47所示，检查是否满足题目要求。

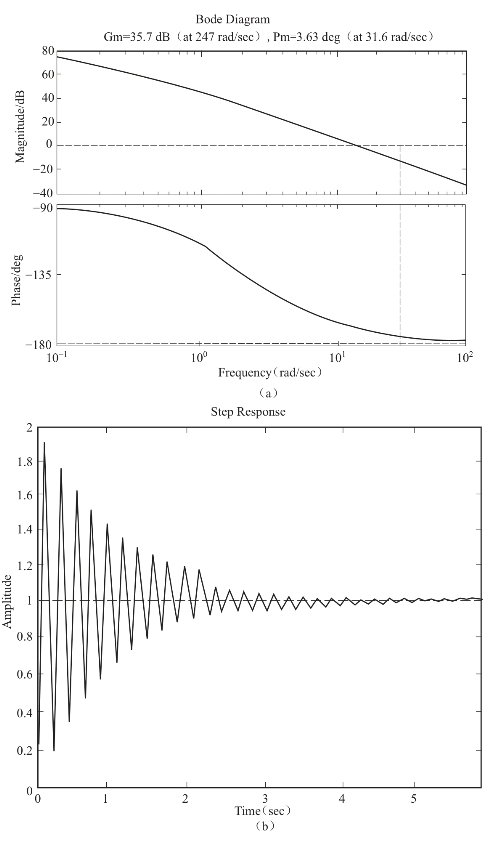
图6-47　未校正系统的波德图及阶跃响应曲线

(a)未校正系统的波德图；(b)未校正系统的阶跃响应曲线

MATLAB程序如下:

由图6-47可知，系统的幅值稳定裕度Gm＝35．7 dB，相位稳定裕度Pm＝3．63°，满足题目中43°＜γ＜48°的要求，此外，系统阶跃响应曲线虽然衰减，但振荡较剧烈，同样不符合要求。

①求超前校正器的传递函数。

根据相位稳定裕度43°＜γ＜48°的要求，取γ＝45°。根据以下程序，计算超前校正传递函数:

MATLAB程序如下:

运行结果:

即校正装

置传递函数为

②检验系统校正后是否满足要求。

根据校正后系统的结构与参数，给出以下MATLAB程序:

如图6-48所示，稳定裕度为Gm＝97．9 dB，Pm＝47．2°。

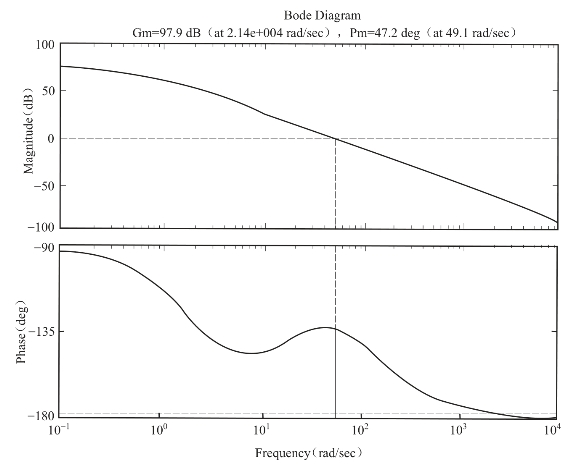
图6-48　校正后系统的波德图

③计算系统校正后阶跃响应及其性能指标。

校正系统响应曲线及性能指标的MATLAB

程序如下:

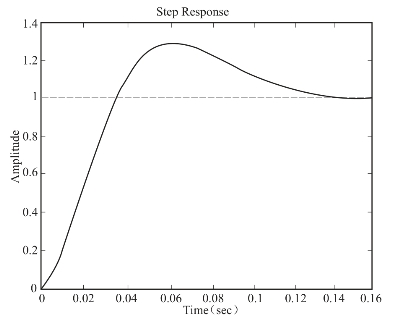
图6-49　校正后系统的阶跃响应曲线

校正后系统阶跃响应曲线如图6-49所示，系统性能指标如下:

σ＝0．295 7，tp＝0．058 7，ts＝0．113 6