为了提高系统的稳态精度，当增大系统的开环增益及提高系统的型别，即增加积分环节的数目时，反而会降低系统的相对稳定性，有时甚至是不稳的。为了解决这对矛盾，应采用复合校正的方法。此种校正方法在高精度的控制系统中得到了广泛的应用。

复合校正中前馈装置是按不变性原理进行设计的，可分为按扰动补偿和按输入补偿两种方式。

1.按扰动补偿的复合校正

按扰动补偿的复合控制系统如图6-39所示。图中，N(s)为可测量的扰动，G0(s)为系统固有特性，Gc(s)为校正装置，Gn(s)为扰动补偿器。Gn(s)的设计原则是，使扰动N(s)经过Gn(s)对系统输出产生补偿作用，以抵消扰动N(s)通过G0(s)对系统输出的影响。我们曾推导过，若选择前馈补偿装置的传递函数

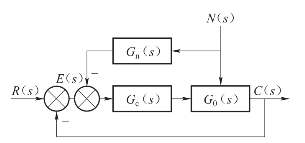
图6-39　按扰动补偿的复合控制系统

则有En(s)＝0。因此，式(6-26)称为对扰动引起误差的全补偿条件。

具体设计时，可以选择Gc(s)的形式与参数，使系统获得满意的动态性能和稳态性能。然后按式(6-26)确定前馈补偿装置的传递函数Gn(s)，使系统完全不受可测量扰动的影响。然而，误差全补偿条件式(6-26)在物理上往往无法准确实现，因为对由物理装置实现的Gc(s)来说，其分母多项式幂次总是大于或等于分子多项式的幂次。因此，在实际使用时，更多地在对系统性能起主要影响的频段内采用近似全补偿，或者采用稳态全补偿，以使前馈补偿装置易于物理上的实现。

从补偿原理看，由于前馈补偿实际上是采用开环控制方式去补偿可测量的扰动信号，因此前馈补偿并不改变反馈控制系统的特性。从抑制扰动的角度来看，前馈控制可以减轻反馈控制的负担，所以反馈控制系统的增益可以取得小一些，有利于系统的稳定性。所有这些都是用复合校正方法设计控制系统的有利因素。

【例6-5】设按扰动补偿的复合校正随动系统如图6-40所示。图中K1为综合放大器的增益，1/(T1s＋1)为滤波器的传递函数，Km/[s(Tms＋1)]为何服电动机的传递函数，N(s)为负载转矩扰动，试设计前馈补偿装置Gn(s)，使系统输出不受扰动影响。

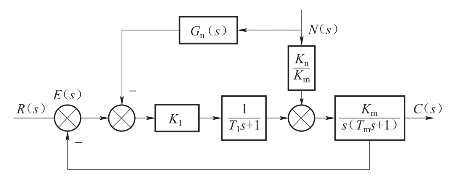
图6-40　带前馈补偿的随动系统

解:由图6-40，可计算出扰动作用下的输出为

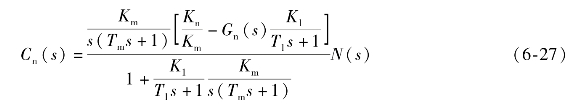
为了使系统输出不受负载转矩扰动的影响，应取Gn(s)为

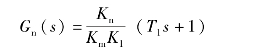
但是，由于Gn(s)的分子幂次高于分母幂次，故不便于物理实现，若令

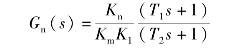
满足T1＞＞T2(类似超前网络在中频段的微分特性(斜率为＋20 dB/deo))，则Gn(s)在物理上是可实现的，且达到近似全补偿要求，即在扰动信号作用的主要频段内进行了全补偿。此外，若取

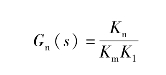
将上式代入式(6-27)，可得(www.daowen.com)

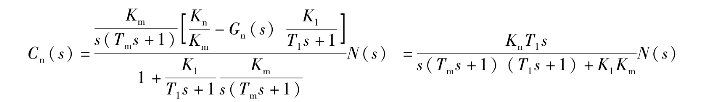
由上式可见，在阶跃扰动下，稳态时系统输出完全不受扰动的影响，这就是所谓稳态全补偿，它在物理上更容易实现。

由上述分析可知，采用前馈控制补偿扰动信号对系统输出的影响，是提高系统控制准确度的有效措施，但是如果用前馈补偿，首先要求扰动信号是可测量的，其次要求前馈补偿量在物理上是可实现的，并力求简单。在实际应用中，多采用近似全补偿或稳态全补偿方案。一般来说，主要扰动引起的误差，由前馈控制进行全部或部分补偿；次要扰动引起的误差，由反馈控制予以抑制。这样，在不提高开环增益的情况下，各种扰动引起的误差均可得到补偿，从而有利于同时兼顾提高系统稳定裕度和减小系统稳态误差的要求。此外，由于前馈控制是一种开环控制，因此要求构成前馈补偿装置的元部件具有较高的参数稳定性，否则将削弱补偿效果，并给系统输出造成新的误差。

2.按输入补偿的复合校正

设按输入补偿的复合控制系统如图6-41所示。图中G0(s)为系统固有特性，Gc(s)为前向校正装置传递函数，Gr(s)为输入补偿器。我们曾推导过，若选择前馈补偿装置的传递函数为

则C(s)＝R(s)，E(s)＝0。表明在式(6-28)成立的条件下，系统输出在任何时刻都完全无误地复现输入，这时系统具有理想的时间响应特性，同时系统在任何时刻的误差都等于零。

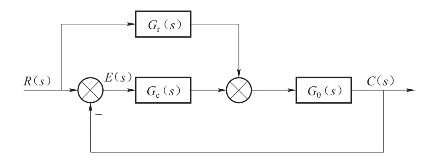
图6-41　按输入补偿的复合控制系统

为了说明前馈补偿装置能够完全消除误差的物理意义，观察图6-41，由于前馈补偿装置的存在，相当于在系统中增加了一个输入信号Gr(s)R(s)，其产生的误差信号与原补偿装置信号R(s)产生的误差信号大小相等符号相反，故称式(6-28)为对输入信号的误差全补偿条件。

由于G0(s)一般具有比较复杂的形式，故全补偿条件的物理实现相当困难。在工程实践中，大多采用满足跟踪精度要求的部分补偿条件，或者在对系统性能起主要影响的频段内实现近似补偿，以使Gr(s)的形式简单并易于实现。

【例6-6】设复合校正的随动系统如图6-42所示。试选择前馈补偿方案和参数进行误差分析。

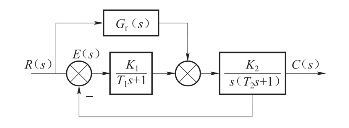
图6-42　按输入补偿的随动系统

解:当Gr(s)＝0时，系统为Ⅰ型，在斜坡输入信号下的稳态误差为常值。系统的误差传递函数为

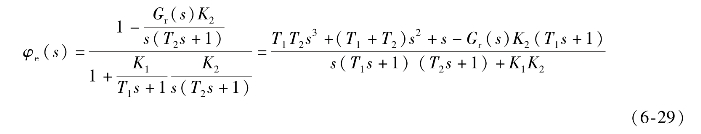
若要求系统在任何输入信号下的误差为零，则需要满足全补偿条件，即

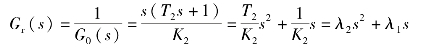
可以看出全补偿的传递函数由输入信号的一阶微分和二阶微分构成。如果取λ1＝1/K2，λ2＝T2/K2，将其代入式(6-29)，可得E(s)＝0。如果λ2＝0，λ1＝1/K2，将其代入式(6-29)可得

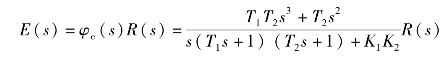
在斜坡输入信号下的稳态误差为零，相当于使系统由Ⅰ型提高为Ⅱ型。