在控制系统的校正中，除了采用串联校正方案外，反馈校正也是常用的校正方式之一。反馈校正除了与串联校正一样，可改善系统的性能以外，还可抑制反馈环内不利因素对系统的影响。常见的有被控量的速度、加速度反馈，执行机构的输出及其速度的反馈，复杂对象的中间变量反馈等，如图6-30所示。

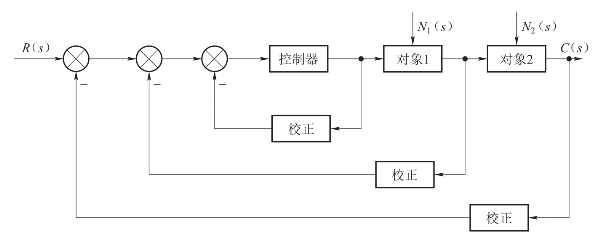
图6-30　反馈校正的连接方式

在随动系统和调速系统中，转速、加速度、电枢电流等都可以作为反馈信号，而具体的反馈元件实际上是一些传感器，如测速发电机、电压加速度传感器、电流互感器等。

选用反馈校正能有效地提高系统的控制精度。下面分几种情况说明。

(1)比例负反馈可以减弱被反馈包围部分的惯性，从而扩展其频带。

比例负反馈包围惯性环节，如图6-31所示，其闭环传递函数为

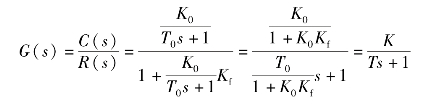
其中

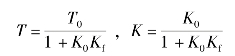
从闭环传递函数的形式看，此种情况仍是惯性环节。因为K0Kf＋1＞1，则T＜T0。即采用比例负反馈的惯性环节，其惯性将有所减弱，减弱程度大致与反馈系数Kf成反比，从而使调节时间ts缩短，提高了系统或环节的快速性。从频域角度看，比例负反馈可使环节或系统的频带得到展宽，其展宽的倍数基本上与反馈系数Kf成正比。然而其增益也将因负反馈而降低，即K＜K0，这是不希望的，可通过提高放大环节的增益得到补偿，即可变为图6-32。只要适当地提高K1的数值即可解决增益减小的问题。

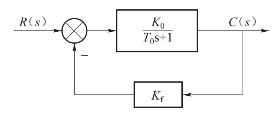
图6-31　比例负反馈(包围惯性环节)

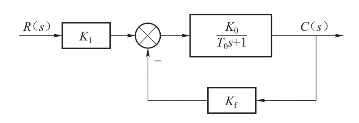
图6-32　系统结构变换图

(2)速度反馈包围振荡环节，可增加环节的阻尼，有效地减弱阻尼环节的不利影响。

图6-33所示系统的闭环传递函数为

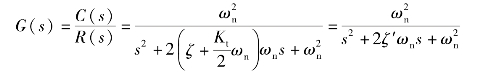
式中，ζ′＝ζ＋ωn，因此ζ′＞ζ，增加了相对阻尼比，改善了系统或环节的平稳性。

速度反馈一般可采用测速发电机来实现，也可采用微分网络来实现。一般情况下得不到纯微分环节，实际上都是存在着小惯性环节的影响，即Kts/(T1s＋1)。只要T1足够小(10－4～10－2)，可认为是纯微分环节，增大阻尼的效果是较显著的。

(3)反馈校正可以减弱参数变化对系统性能的影响。

在控制系统中，为了减弱系统对参数变化的敏感度，一般多采用负反馈校正，如图6-34所示，比较有反馈和无反馈时系统输出对参数变化的敏感程度。

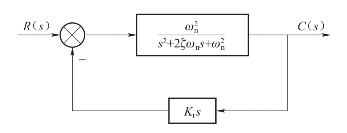
图6-33　速度反馈(包围振荡环节)

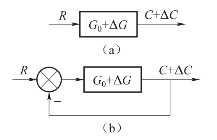
图6-34　系统结构图

(a)无反馈；(b)有反馈

由于元部件参数变化而引起G0(s)的变化为ΔG(s)，相应的输出变化为ΔC(s)。对于开环系统，有

即

就是说，对于开环系统，由于参数变化引起输出的变化量与传递函数的变化量ΔG(s)成正比。(www.daowen.com)

而对于负反馈包围的局部系统，有

一般情况下，，于是近似有

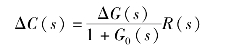
由于负反馈的包围，参数变化引起输出变化量ΔC(s)约是开环系统的。在系统工作的主要频段内，通常的值远大于1，因此负反馈能明显地减弱参数变化对控制系统性能的影响。

用负反馈包围局部元部件的校正方法在电液伺服系统中经常被采用。

(4)负反馈校正取代局部结构，消除系统不可变部分中不希望有的特性。图6-35所示的局部回路的传递函数为

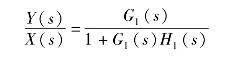
频率特性为

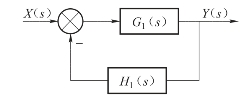
图6-35　系统结构图

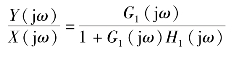
如果在常用的频段内选取

则在此频段内

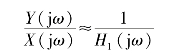
该式说明，如果在满足＞＞1的频段内，G1(jω)是不希望的，那么就可以选择H1(jω)组成的特性，利用这种“置换”办法可以改善系统的性能。

【例6-4】利用二阶微分环节包围电液伺服系统的局部环节来改善系统性能，如图6-36所示。

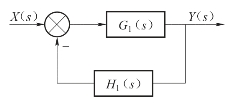
图6-36　例6-4系统结构图

解:把图6-36等效变换为图6-37。适当地选取τ1和ζ1，最好能使ζ1＝0．707。若原系统中的ζ1较小且变化，大致绘出Y(s)/R(s)的根轨迹如图6-38所示。

图6-37　系统结构变换图

当此时根轨迹增益选取较大时，s1、s2靠近z1、z2而成为偶极子，主导极点变为s2、s3远离虚轴，则｜s3｜＞＞1，这时，Y(s)/R(s)成为小惯性环节，即

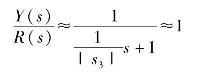
则系统变为

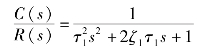
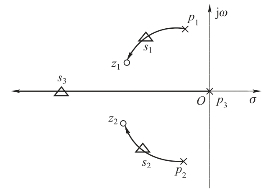
图6-38　系统根轨迹图

成为最佳二阶系统模型，使系统的动态性能得到很大改善。原系统中所不希望的结构由反馈传递函数的倒数所取代。

在大功率的电液伺服系统中，以及一些变载荷及测试系统中，都经常采用局部反馈校正的方法。