利用波德图的叠加特性，可以比较方便地在原系统波德图上，添加超前校正网络的波德图。其设计步骤如下:

(1)绘制未校正系统的波德图，计算相位裕度，判定是否满足要求，是否需要引入合适的超前校正网络Gc(s)。

(2)确定所需的最大超前相角φm。

(3)利用sinφm＝计算α。

(4)计算10lgα，在未校正系统的幅值增益曲线上，确定一个与－10lgα对应的频率。当ω＝ωc＝ωm时，超前校正网络能提供10lgα(dB)的幅值增量，因此，经过校正后，原有幅值增益为－10lgα的点将变成新的0 dB线的交点，对应频率就是新的转折频率ωc＝ωm。

(5)计算极点频率｜p｜＝ωm和零点频率｜z｜＝｜p｜/α＝ωm/。

(6)绘制校正后的闭环系统波德图，检查系统是否满足要求。若不满足要求，则重新设计。

(7)确定系统的增益，以保证系统的稳态精度，抵消由超前校正网络带来的衰减1/α。

【例6-1】考虑开环传递函数为G0(s)＝　

的系统，希望稳态误差系数Kv≥100 s－1，相位裕度γ≥30°，且穿越频率ωc≥45 rad/s。解:由于该系统为Ⅰ型，因此选择

K＝Kv＝100 s－1

具体步骤如下:

(1)如图6-22所示，绘制未校正系统的波德图。

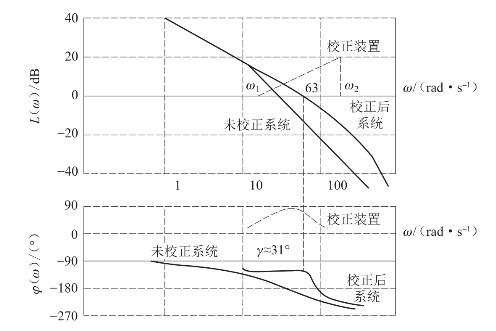
图6-22　例6-1的波德图

(2)在本例中，校正后的穿越频率应当满足响应速度的要求。如果选择ωc＝50 rad/s，则G0(jω)在该频率处的相角为

∠G0(jω)ω＝50＝－90°－arctan(0．1×50)－arctan(0．01×50)＝－195°

(3)因为希望相位裕度γ≥30°，所以，所需的超前相角至少为(www.daowen.com)

30°－(180°－195°)＝45°

在留有余地的情况下，选择由校正装置提供的超前相角为φm＝55°。

(4)可求α值为

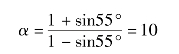
得超前校正网络的两个转折频率为

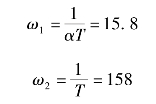
因此，校正装置的传递函数为

(5)校正装置和校正后系统的波德图如图6-22所示。

(6)由

而由图6-22则有

这样校正后实际的穿越频率大于ωm＝50 rad/s，由图6-22可看到合适的校正后穿越频率为

因此，最终的相位裕度为

γ＝180°＋∠G0(jω′c)＋∠Gc(jω′c)＝180°－203．2°＋54．3°＝31．1°

最终的相位裕度大于相位裕度的期望值。