常用的串联校正网络的传递函数一般形式为:

于是，校正装置的设计转化为网络的零极点的配置问题。当校正网络为1阶时，传递函数为

Gc(s)的设计问题变成了参数K、z、p的取值问题。当时，称校正网络为相角超前校正网络，简称超前校正网络，它在s平面的零极点分布如图6-17(b)所示。

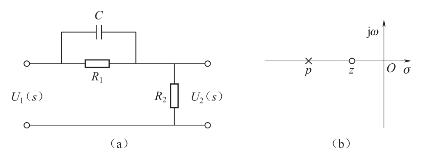
图6-17　超前校正网络

(a)电路图；(b)零极点分布

超前校正网络的频率特性函数为

其中，τ＝1/，p＝αz，K1＝K/α，

超前校正网络对应的相频特性曲线为

φ(ω)＝arctan(αωτ)－arctan(ωτ)

(6-15)

图6-18给出了超前校正网络K1＝1的波德图。从图中可看出，在零点频段附近，超前校正网络的相角为正，幅值增益渐近线斜率为20 dB/dec，表明超前校正网络能为原系统提供附加超前相角。

超前校正网络的典型电路如图6-17(a)所示，该电路的传递函数为

图6-18　超前校正网络的波德图

令τ＝，则

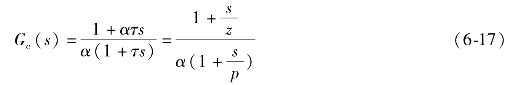
没有增益参数K。(www.daowen.com)

设ωm为极点p＝1/τ和零点z＝1/(ατ)的几何平均数，即在对数尺度的频率轴上，最大超前相角出现在极点频率和零点频率的中点处，有

由式(6-15)可得超前校正网络的相角值为

将式(6-18)代入式(6-19)，得

或

这是最大超前相角计算公式，在设计过程中，如果知道了预期的最大超前相角，就可以利用上式计算所需的网络参数α。图6-19给出了φm与α的关系曲线，从中可看出φm不会超过70°。另外，由于α＝(R1＋R2)/R2，所以α也存在着实际电阻值的限制。因此，实际上一阶超前校正网络的φm值不会超过70°。

另一种常用的串联校正网络是相角滞后校正网络(或称滞后校正网络)，它为原有系统带来滞后相角。滞后校正网络典型电路如图6-20(a)所示，零极点分布如图6-20(b)所示。其传递函数为

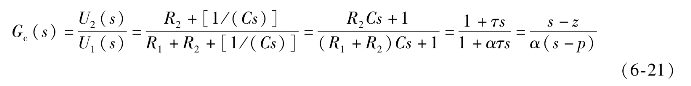
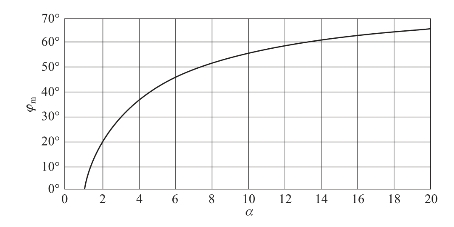
图6-19　一阶超前校正网络的最大超前角φm与α的关系

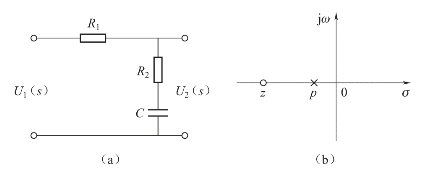
图6-20　滞后校正网络及其零极点图

其中

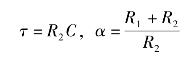
滞后校正网络的频率特性为Gc(jω)＝，对应的波德图如图6-21所示。

图6-21　滞后校正网络的波德图

从图6-21可看出，相角为负，幅值增益随频率增大而衰减。最大滞后相角的对应频率为ωm＝。

在控制系统设计中，接入串联校正网络可以使闭环系统有期望的频率响应。超前校正网络的主要作用是提供一个超前相角，从而增大闭环系统的相位裕度，工程上主要用于改善控制系统的稳定性和快速性。滞后校正网络的主要作用不是引入一个滞后相角，而是要幅值增益适当衰减，工程上可用来提高系统的稳态精度和稳定性，但缺点是降低了系统的快速性。