基于频域稳定性判据在波德图上的描述，可以在波德图上定义两个性能指标，称为稳定裕度，或稳定余度、稳定余量、稳定裕量等。开环系统的波德图上有两个稳定裕度，一个称为幅值裕度Lg，另一个称为相位裕度γc，下面分别进行介绍。

1.幅值裕度h(Lg)

如图5-42和图5-43所示，令幅相曲线穿越－180°相位线所对应的频率为ωg，这个频率称为相角穿越频率，此频率所对应的幅值为A(ωg)。把相角穿越频率对应的幅频特性A(ωg)的倒数称为幅值稳定裕度，简称幅值裕度，即

h＝1/A(ωg)　或　h×A(ωg)＝1

(5-80)

图5-42　极坐标图上稳定裕度示意图

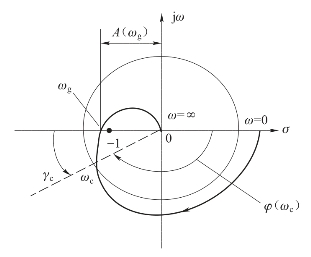
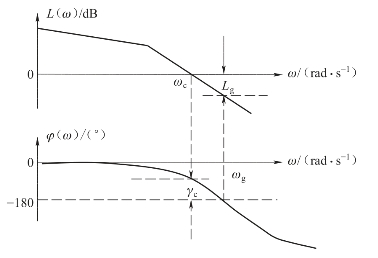
图5-43　波德图上的稳定裕度示意图

在对数坐标图上，采用Lg表示h的分贝值，即

Lg＝20lgh＝20lg[1/A(ωg)]＝－20lgA(ωg)dB

(5-81)

幅值裕度的物理意义:对于稳定的系统，若系统的开环放大倍数再增大为原来的h倍(或对数幅频特性曲线向上移动Lg分贝)，则系统就将变为临界稳定状态；若开环放大倍数再进一步增大，则系统将变为不稳定；反之亦然。

2.相位裕度γc

令幅相曲线穿越单位圆或对数幅频特性趋向穿过0 dB线所对应的频率为ωc，这个频率称为幅值穿越频率，此频率所对应的相位为φ(ωc)。把幅值穿越频率ωc对应的相频特性φ(ωc)与－180°之差称为相位稳定裕度，简称相位裕度，即

γc＝φ(ωc)－(－180°)＝180°＋φ(ωc)

(5-82)

相位裕度的物理意义:如果系统是稳定的，若相频特性φ(ωc)再滞后γc角度(或对数相频特性φ(ω)再下移γc角度)，则闭环系统将变为临界稳定状态；若对数相频特性φ(ω)再进一步减小，则系统将变为不稳定；反之亦然。

3.利用稳定裕度判别系统稳定性

对于最小相位系统来说，Lg＞0和γc＞0总是同时发生或同时不发生，因此工程上常只用相位稳定裕度γc来表示。显然，系统稳定时，必有Lg＞0和γc＞0。

【例5-12】已知单位反馈的最小相位系统，其开环对数幅频特性如图5-44所示，试求开环传递函数，并计算系统的稳定裕度。

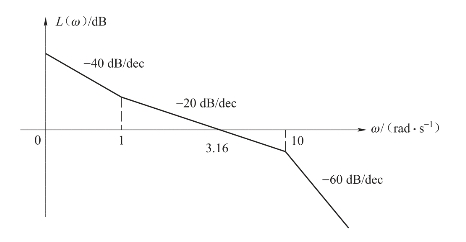
图5-44　例5-12开环对数幅频特性曲线

解:(1)由给定的对数幅频特性可以求得开环传递函数为(www.daowen.com)

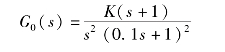
(2)计算放大倍数K:

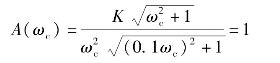
考虑到ωc＝3．16＞1，所以1，(0．1ωc)2＜＜1，于是，上式可以简化为

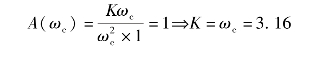
或

(3)计算稳定裕度。

①相位裕度:

γc＝180°＋φ(ωc)＝180°＋arctanωc－2×90°－2×arctan0．1ωc

＝180°＋arctan3．16－2×90°－2×arctan(0．1×3．16)

＝180°＋72．40°－180°－2×17．5°

＝37．4°

②幅值裕度:

由φ(ωg)＝－180°可得

arctanωg－2×90°－2×arctan0．1ωg＝－180°

化简得到arctanωg＝2×arctan0．1ωg。令φ＝arctan0．1ωg，则:

tan(arctanωg)＝tan(2×arctan0．1ωg)＝tan2φ

由三角公式可得

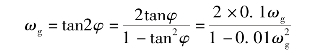
解得ωg＝8．94(rad/s)。于是幅值稳定裕度为

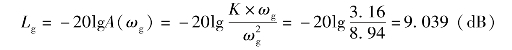
显然，由于Lg＞0，γc＞0所以闭环系统稳定。