由式(5-55)可知,该式包括比例因子、一阶因子和二阶共轭复数因子,都是基本环节,所以G0(jω)的一般表达式可以写为基本因子的乘积,即
![]()
采用模、相角表达式可表示为
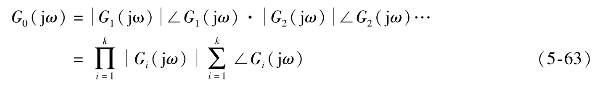
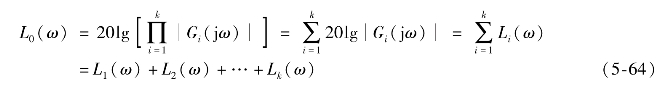
开环对数相频特性为
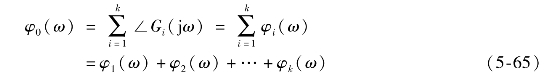
式(5-64)和式(5-65)说明了L0(ω)和φ0(ω)分别都是各典型环节的叠加。
通过以上的分析,可以采用典型环节叠加作图和转折渐近作图两种方法来绘制控制系统的开环对数频率特性图。典型环节叠加作图方法是分别作出各基本环节的Li(ω),在图上叠加得到L0(ω),以及分别作出各基本环节的φi(ω),在图上叠加得到φ0(ω)。而转折渐近作图主要是依照转折渐近表作出L0(ω),而开环对数相频特性φ0(ω)仍然要依照叠加方法作图。但是从后面的分析可以看到,在许多情况下,可以省略φ0(ω)的作图。这样,转折渐近作图就又快又方便了。因此,通常使用更多的还是转折渐近作图方法。
转折渐近作图具体步骤可归纳如下:
(1)将开环传递函数写成尾一型标准形式;
(2)根据比例环节,求出20lgK0;
(3)过ω=1,L(ω)=20lgK0,即(1,20lgK0)作一条斜率为-20ν dB/dec的斜线(ν是积分环节的个数);
(4)计算各典型环节的转折频率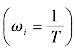 ,并按ωi由小到大的顺序,依次改变各对应频段的斜率,并依次叠加,即得出最后的对数幅频特性。
,并按ωi由小到大的顺序,依次改变各对应频段的斜率,并依次叠加,即得出最后的对数幅频特性。
(5)作各环节对数相频特性,并依次叠加得到最后的对数相频特性。
【例5-3】系统开环传递函数为G0(s)= ![]() ,试绘制系统对数幅频特性曲线的渐近线。
,试绘制系统对数幅频特性曲线的渐近线。
解:(1)由于该系统为I型系统,低频段延长线与实轴交点为K0=4;
(2)过(4,0)作斜率为-20 dB/dec的斜线;
(3)求各转折频率并作表:

(4)依次作图,得到曲线如图5-26所示。(www.daowen.com)
【例5-4】已知单位负反馈系统的开环传递函数为G0(s)=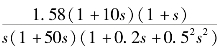 ,试作出该系统的对数开环频率特性曲线。
,试作出该系统的对数开环频率特性曲线。
解:(1)首先,把开环传递函数化为尾一型标准形式,其次,求20lgK0=20lg1.58=3.97 dB;
(2)过(1,3.97)作斜率为-20ν dB/dec=-20 dB/dec的斜线;
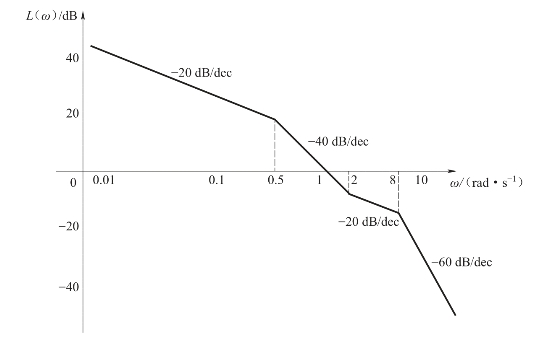
图5-26 例5-3系统的对数幅频特性曲线
(3)求各转折频率并作表:

(4)依次作图,得到曲线如图5-27所示。
另外,由于二阶振荡因子的阻尼比为ζ=0.2,在谐振频率ωr=![]() =1.918处,谐振峰值为
=1.918处,谐振峰值为
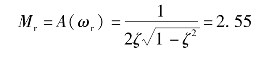
对数峰值为
20lg2.55=8.13 dB≈8 dB
在图上作谐振峰值修正曲线如图5-27所示。
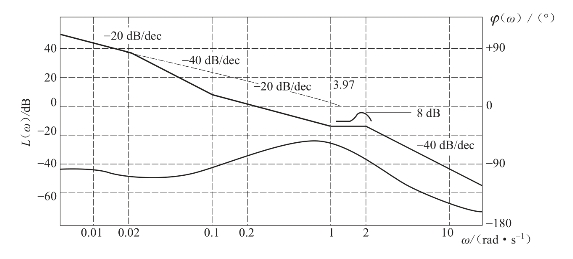
图5-27 例5-4系统的波德图
【例5-5】已知系统的开环对数幅频特性如图5-28所示,试确定系统的开环传递函数。
解:由图5-28可见,低频段的斜率为-20 dB/dec,所以开环传递函数有一个积分环节。由于在低频段ω=1时,L(ω)=15 dB,所以系统的开环放大倍数为满足20lgK=15,从而求得K=1015/20=100.75=5.6。
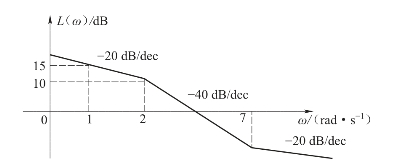
图5-28 例5-5系统的开环对数幅频特性曲线
由此可以写出系统的开环传递函数为
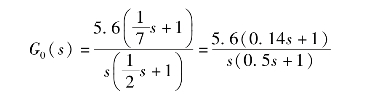
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






