根据系统开环频率特性G0(jω)的表达式，可以通过取点、计算来绘制系统极坐标图，用于进行系统的定性分析，这里结合工程需要，着重介绍绘制概略极坐标图的方法。

由于线性定常系统分子多项式与分母多项式均为常数，可将开环传递函数G0(jω)的分子多项式和分母多项式做因式分解如下:

1.极坐标图的起点

极坐标图的起点是ω→0时G0(j0＋)在复平面上的位置。当前向通路积分环节的个数ν

大于0且ω→0时有

幅值大小为

相角大小为

所以极坐标图的起点位置与前向通路积分环节的个数ν有关。ν为不同值时，极坐标图的起点位置如图5-21所示。

2.极坐标图的终点

极坐标图的终点是ω→＋∞时G0(＋j∞)在复平面上的位置，当ω→＋∞时有

幅值大小为

相角大小为

所以极坐标图终点的入射角度是不同的，入射角度的大小由分母多项式的次数与分子多项式次数之差n－m来决定。各种趋近情况如图5-22所示。

3.坐标轴穿越点与单位圆穿越点

坐标轴穿越点与单位圆穿越点如图5-23所示。这两类穿越除了要确定穿越位置之外，还需要做如下考虑。

在坐标轴穿越点邻域需要确定的是ω＝ωx时，G0(jωx)是以角度增加方式还是以角度减少的方式穿越坐标轴。

在单位圆穿越点邻域需要确定的是ω＝ωy时，G0(jωy)是以幅值增加方式还是以幅值减少的方式穿越单位圆。

(www.daowen.com)

图5-21　极坐标图的起点

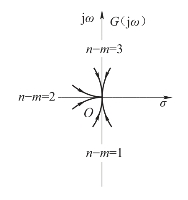
图5-22　极坐标图的终点图

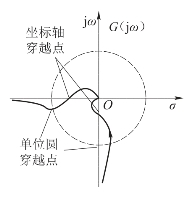
图5-23　极坐标图的穿越点

在不需要准确地作图时，根据上述三条，可以定性地作出开环频率特性G0(jω)的极坐标草图。

【例5-1】已知单位负反馈开环传递函数为G0(s)＝　，试作其极坐标草图。

解:由于ν＝1，有，所以起点位于负虚轴无穷远处。

由于n－m＝2，有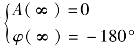，所以曲线以相角－180°趋于原点。相角为φ(ω)＝－90°－∠(1＋jω)，当ω增加时，φ(ω)是单调减的。由以上定性分析，可以作出极坐标草图，如图5-24(a)所示。

当然，该系统比较简单，可以写出它的实部函数与虚部函数表达式来比较准确地描点作图。

图5-24　例5-1的极坐标图

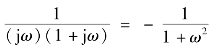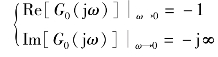由于G0(jω)＝　－j　，所以有和

当ω→0时，实部函数有渐近线为－1，可以先作出渐近线，然后描点将极坐标图作出，如图5-24(b)所示。图5-24中的两图看上去差别较大，但是应用该图作系统分析时，从定性分析的观点来看差别不大，也就是说图5-24(a)趋势作图的粗略性，基本不影响该图在系统分析时的应用。

【例5-2】已知单位反馈控制系统的开环传递函数为Gk(s)＝　，试概略绘制系统开环幅相曲线。

解:由于N＝2为Ⅱ型系统，根据极点－零点分布图(见图5-25)，显然

(1)起点Gk(j0)＝∞∠－180°；

(2)终点Gk(j∞)＝0∠－270°；

(3)与坐标轴的交点

当ω2x＝0．5，即ωx＝0．707时，极坐标图与实轴有一交点，交点坐标为

Re(ωx)＝－2．67K

因为Re(ω)＜0，当ω＜ωx时，Im(ω)＜0；当ω＞ωx，时，Im(ω)＞0，所以极坐标图应在第Ⅲ象限和第Ⅱ象限，开环概略极坐标图如图5-25所示。把ω＝0．707这点的概率也称为相角穿越频率，常记作ωg，此时φk(ωg)＝－180°。

图5-25　例5-2极点－零点分布图和幅相曲线