采用根轨迹法分析或设计线性控制系统时，了解闭环零点和实数主导极点对系统性能指标的影响，是非常重要的。

1.闭环零点对系统性能的影响

例如某一控制系统，由于闭环零点的存在，将使系统的峰值时间提前，这相当于减小闭环系统的阻尼，从而使超调量加大，当闭环零点接近坐标原点时，这种作用尤甚。对于具有一个闭环实数零点的振荡二阶系统，不同零点位置与超调量之间的关系曲线，如图4-16所示。一般来说，闭环零点对调节时间的影响是不定的。

2.闭环实数主导极点对系统性能的影响

闭环实数主导极点的作用，相当于增大系统的阻尼，使峰值时间滞后，超调量下降。如果实数极点比共轭复数极点更接近坐标原点，甚至可以使振荡过程变为非振荡过程。闭环实数极点的这种作用，可以用下面的物理浅释来说明:显然，无零点三阶系统相当于欠阻尼二阶系统与一个滞后的平滑滤波器的串联，因此欠阻尼二阶系统的时间响应经过平滑滤波器后，其峰值时间被滞后，超调量被削弱，过渡过程趋于平缓。实数极点越接近坐标原点，意味着滤波器的时间常数越大，上述这种作用越强。

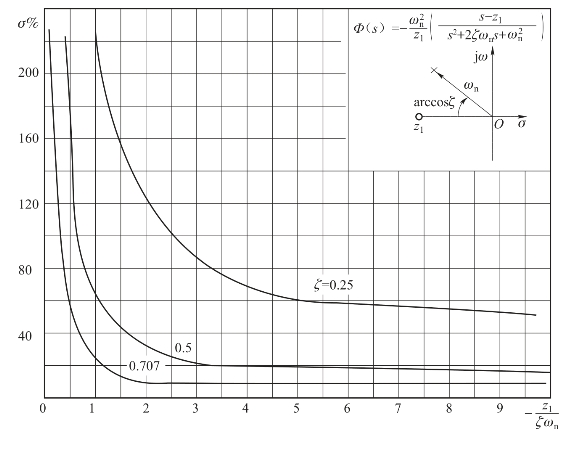
图4-16　零点相对位置与超调量的关系曲线

闭环系统零、极点位置对时间响应性能的影响，可以归纳为以下几点:(www.daowen.com)

(1)稳定性。如果闭环极点全部位于s左半平面，则系统一定是稳定的，即稳定性只与闭环极点位置有关，而与闭环零点位置无关。

(2)运动形式。如果闭环系统无零点，且闭环极点均为实数极点，则时间响应一定是单调的；如果闭环极点均为复数极点，则时间响应一般是振荡的。

(3)超调量。超调量主要取决于闭环复数主导极点的衰减率为闭环复数主导极点的实部绝对值)，并与其他闭环零、极点接近坐标原点的程度有关。

(4)调节时间。调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值σ1＝ζωn，σ1越大，调节时间越短。如果实数极点距虚轴最近，并且它附近没有实数零点，则调节时间主要取决于该实数极点的幅值。

(5)实数零、极点影响。零点减小系统阻尼，使峰值时间提前，超调量增大；极点增大系统阻尼，使峰值时间滞后，超调量减小。它们的作用，随着其本身接近坐标原点的程度而加强。

(6)偶极子及其处理。如果零、极点之间的距离比它们本身的幅值小一个数量级，则它们就构成了偶极子。远离原点的偶极子，其影响可略；接近原点的偶极子，其影响必须考虑。

(7)主导极点。在s平面上，最靠近虚轴而附近又无闭环零点的一些闭环极点，对系统性能影响最大，称为主导极点。凡比主导极点的实部大6倍以上的其他闭环零、极点，其影响均可忽略。