如果研究的系统的根轨迹方程的右侧不是“－1”而是“＋1”，这时根轨迹方程的幅值方程不变，而相角方程右侧不再是“(2k＋1)π”，而是“2kπ”，因此这种根轨迹称为零度根轨迹。这种情况主要来源于正反馈系统和某些非最小相位系统，关于非最小相位系统的概念在下一章介绍。

零度根轨迹的绘制法则与常规根轨迹绘制法则略有不同。以正反馈系统为例:设某复杂控制系统如图4-15所示，其中内回路采用正反馈。为了分析整个控制系统的性能，需要求出内回路的闭环零、极点。可以用根轨迹的方法，这样就要绘制正反馈系统的根轨迹。

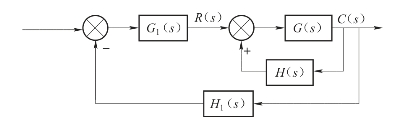
图4-15　复杂控制系统

系统中正反馈回路的闭环传递函数为

正反馈回路的特征方程为

D(s)＝1－G(s)H(s)

(4-31)

正反馈回路的根轨迹方程为

G(s)H(s)＝1

(4-32)(www.daowen.com)

将式(4-32)写成相角方程和幅值方程的形式，相角方程为

幅值方程为

将式(4-33)和式(4-34)与常规根轨迹方程式(4-11)和式(4-12)相比，显然幅值方程相同，而相角方程不同。因此，使用常规根轨迹法绘制零度根轨迹时，对于与相角方程有关的某些法则要进行修改，应修改的法则如下:

【法则3】实轴上某一区域，若其右方开环实数零、极点个数之和为偶数，则该区域必是根轨迹的一部分。

【法则4】根轨迹的渐近线与实轴的夹角和交点为

σα计算公式不变

【法则6】根轨迹的出射角与入射角:

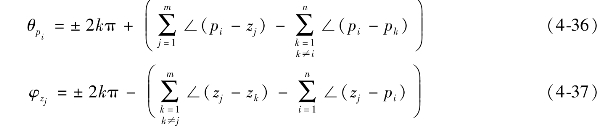
除上述三个法则外，其他法则不变。