【法则1】根轨迹的分支数、起点和终点:有n个开环极点、m个开环零点的系统

(n≥m)，根轨迹的分支有n条，它们分别起始于n个开环极点，有m条终止于开环零点，尚有n－m条终止于无穷远处的零点。

注:若特征方程中，m≥n，则方程的阶数与m、n中大者m相同，则根轨迹的分支数也与m相同，根轨迹起始于n个开环极点和(n－m)个无穷远处的极点，而终止于m个开环零点。

【法则2】根轨迹的连续性和对称性:根轨迹连续且关于实轴对称。

由于根轨迹增益kg由0→∞的变化是连续的，所以系统闭环特征方程的根也是连续变化的，即s平面上的根轨迹是连续的。

由于线性定常系统闭环特征方程的系数全部是实数，其根必为实数或共轭复数，所以s平面上的根轨迹图是实轴对称的。

【法则3】实轴上的根轨迹:实轴上的根轨迹完全由实轴上的开环极点和零点所确定。若某段实轴右侧的实极点数与实零点数之和是奇数，则这段实轴就是根轨迹的一部分；若某段实轴右侧的实极点数和实零点数之和为偶数，则它不是系统的根轨迹。

设某一系统的开环零、极点分布如图4-4所示，若实轴上某一点是根轨迹上的点，它必满足相角方程式(4-12)。在实轴上任取一实验点s1，由图4-4可见，在复平面上任何一对共轭复数极点(或零点)到s1处向量的相角之和为零，如图4-4上∠(s1＋p2)＋∠(s1＋p3)＝0。而实验点s1左侧实轴上的开环零、极点到s1处向量的相角也为零，所以它们都不影响相角方程的成立。只需考虑实验点s1右侧实轴上开环零、极点到s1点处向量的相角，每个相角都为π。将上述关系代入相角方程式(4-12)中，则

＝∠(s1＋z1)＋∠(s1＋z2)－∠(s1＋p1)

＝π＋π－π

＝π

＝(2k＋1)π　　(k＝0)

所以相角方程成立，即s1是根轨迹上的点。而且s1右侧有两个开环零点，一个开环极点，则它们数目之和为奇数。一般情况，设实验点右侧有l个开环零点，h个开环极点，则有关系式

图4-4　实轴上的根轨迹

若满足相角条件，必有关系式

(l－h)π＝(2k＋1)π

【例4-2】设一单位负反馈系统的开环传递函数为G0(s)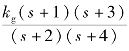＝，求kg＝0→∞时闭环系统根轨迹。

解:系统开环传递函数有两个开环零点，z1＝－1，z1＝－3；两个开环极点，p2＝－2，p1＝－4。开环传递函数分子的阶数m＝2，分母的阶数n＝2。首先将开环零、极点布置在s平面上，如图4-5(a)所示，然后按绘制根轨迹的基本法则逐步画出根轨迹。

(1)由法则1可知有两条根轨迹，分别起始于开环极点－2、　－4，终止于有限零点－1、　－3。

(2)依据法则2，两条根轨迹对称于实轴且连续。

(3)依据法则3，在负实轴上，　－4到－3之间和－2到－1之间是根轨迹。最后绘制出的根轨迹如图4-5(b)所示。

图4-5　例4-2系统的根轨迹图

【法则4】根轨迹的渐近线:根轨迹的渐近线与实轴的夹角φα和与实轴的交点σα由下式确定

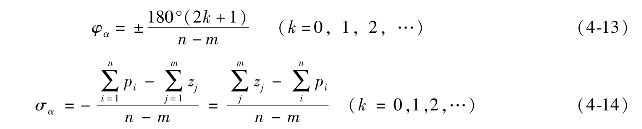
证明:假设在无穷远处有特征根sk，则s平面上所有开环有限零点zj和极点pi到sk的矢量相角相等，即

∠(sk－zj)＝∠(sk－pi)＝φα

代入相角条件

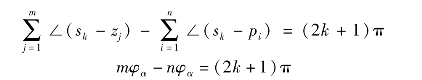
π与－π是等同的，因此

考虑到s平面上所有开环有限零、极点到无穷远处特征根sk的矢量长度都相等，于是，对于sk而言，所有开环有限零、极点都汇集在一起，其位置为实轴上一点σα，得

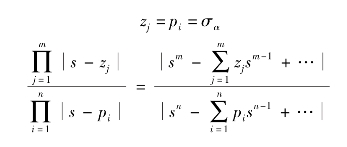
即

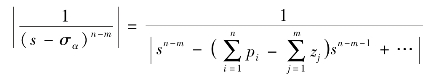
令上式中sn－m－1项系数相等，得

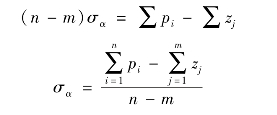
【例4-3】已知控制系统的开环传递函数为G0(s)＝　，试确定根轨迹的分支数、起点和终点。若终点在无穷远处，试确定渐近线与实轴的交点及渐近线的倾斜角。

解:由于n＝3，所以有3条根轨迹，起点分别在p1＝0，p2＝－1和p3＝－2。由于m＝0，开环传递函数没有有限值零点，所以三条根轨迹的终点都在无穷远处，其渐近线与实轴的交点σα及倾斜角φα分别为

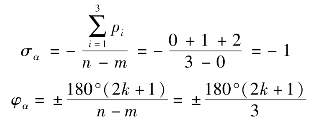
当k＝0时，φα＝±60°；当k＝1时，φα＝±180°；根轨迹的起点和三条渐近线如图4-6所示。

【法则5】根轨迹的分离点:两条或两条以上的根轨迹分支在s平面上相遇又立即分开的点，称为根轨迹的分离点。分离点的坐标是下列方程的解:式中，zj为各开环零点的数值；pi为各开环极点的数值；d为分离点坐标。

式(4-15)采用的试探法求解。之外，还可用重根法等求取分离点，关于公式的证明可以参阅其他参考教材。

根轨迹的分离点或位于实轴上，或以共轭形式成对出现在复平面中。如果根轨迹位于实轴上两个相邻的开环极点之间，则在这两个极点之间至少存在一个分离点；同样，如果根轨迹位于实轴上两个相邻的开环零点(有限零点或无穷零点)之间，则在这两个零点之间至少存在一个分离点。

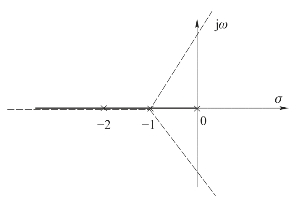
图4-6　根轨迹渐近线图

如图4-7所示为某系统的根轨迹图，实轴上有两个交点A和B，分别称为根轨迹在实轴上的分离点。

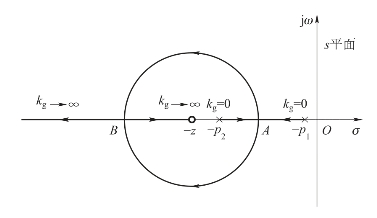
图4-7　根轨迹上的分离点

在分离点上，根轨迹的切线和实轴的夹角称为分离角。分离角θd与相分离的根轨迹的分支数k有关，即

例如，实轴上两支根轨迹的分离角为±90°。三支根轨迹的分离角为0°、　±60°、　±180°。式(4-16)的分离角公式可以由相角条件公式证得。

图4-8绘出了四支根轨迹在实轴上分离的情况。图4-9绘出了在复平面上有分离点的情况，复平面上的分离点是关于实轴对称的。

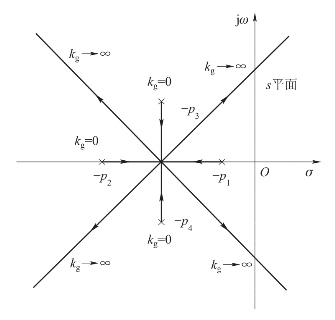
图4-8　四重根的分离点

图4-9　复平面上分离点

【例4-4】设控制系统结构图与开环零、极点分布如图4-10所示，试绘制其概略根轨迹。

解:由法则1可知，系统有3条根轨迹分支，分别起始于(0，j0)、(－2，j0)、(－3，j0)点，一条终止于(－1，j0)点，另外两条止于无穷远处。

由法则2可知，根轨迹连续且关于实轴对称。

由法则3可知，实轴上区域[0，　－1]和[－2，　－3]是根轨迹，在图4-10中以粗实线表示。

图4-10　例4-4系统的结构图及其根轨迹图

(a)结构图；(b)根轨迹图

由法则4可知，两条终止于无穷的根轨迹的渐近线与实轴的夹角和交点坐标为

由法则5可知，实轴上[－3，－2]必有一个分离点，满足下列分离点方程:

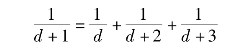
初步试探，设d＝－2．5，上式中左边＝－0．67，右边＝－0．4，因方程两边不等，所以d＝－2．5不是分离点。现在重取d＝－2．47，上式中左边＝－0．68，右边＝－0．65，方程两边近似相等，故本例d≈－2．47。最后画出的系统概略根轨迹如图4-10(b)所示。

【法则6】根轨迹的出射角和入射角:当系统的开环极点和零点位于复平面上时，根轨迹离开共轭复数极点的角称为根轨迹的出射角，根轨迹趋于共轭复数零点的角称为根轨迹的入射角。根轨迹的出射角和入射角可用如下公式确定:

(www.daowen.com)

证明:在十分靠近待求起始角的复数极点pi的根轨迹上，取一点s1。由于s1无限接近复数极点pi，因此，除pi外，s1点到其他所有开环零、极点矢量相角都可以用pi到它们的矢量相角来代替，而s1点到pi的矢量相角即为起始角θpi。根据s1必满足相角条件，应有

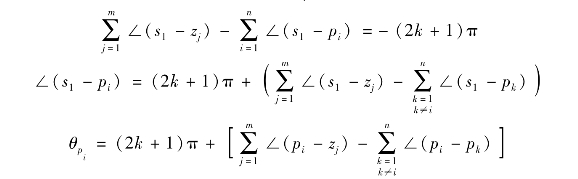
同理，可证明式(4-18)。应当指出，在根轨迹的相角条件中，(2k＋1)π与－(2k＋1)π是等价的，所以为了便于计算，上式右端用了－(2k＋1)π表示。

【例4-5】设系统开环传递函数为G0(s)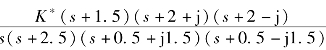＝　，试绘制该系统概略根轨迹。

解:将开环零、极点画在图4-11中。按如下步骤绘制根轨迹:

(1)定实轴上的根轨迹。本例实轴上区域[0，　－1．5]和[－2．5，　－∞]为根轨迹。

(2)确定根轨迹的渐近线。本例n＝4，m＝3，故只有一条趋于180°的渐近线，它正好与实轴上的根轨迹区域[－2．5，　－∞]重合，所以在n－m＝1的情况下，不必再去确定根轨迹的渐近线。

(3)确定分离点。一般来说，如果根轨迹位于实轴上一个开环极点和一个开环零点(有限零点或无限零点)之间，则在这两个相邻的零、极点之间，或者不存在任何分离点，或者同时存在离开实轴和进入实轴的两个分离点。本例无分离点。

(4)确定出射角与入射角。本例概略根轨迹如图4-11所示，为了比较准确地画出这一根轨迹图，应当确定根轨迹的出射角和入射角的数值。先求出射角。作各开环零、极点对(－0．5＋j1．5)的向量，并算出相应角度，如图4-12(a)所示。按式(4-17)算出根轨迹在极点(－0．5＋j1．5)处的出射角为

θp2＝180°＋(φ1＋φ2＋φ3)－(θ1＋θ3＋θ4)＝79°

根据对称性，根轨迹在极点(－0．5－j1．5)处的出射角为－79°。

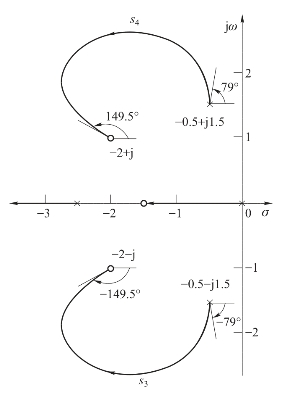
图4-11　例4-5系统的概略根轨迹图

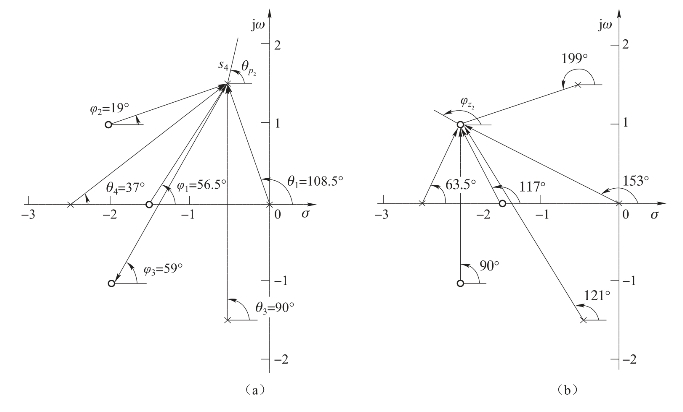
图4-12　例4-5根轨迹的出射角和入射角

(a)出射角；(b)入射角

用类似方法可算出根轨迹在复数零点(－2＋j)处的入射角为149．5°。各开环零、极点到(－2－j)的矢量相角如图4-12(b)所示。

【法则7】根轨迹与虚轴的交点:根轨迹与虚轴相交，对应于系统闭环处于临界稳定状态，根轨迹与虚轴的交点可用劳斯判据求得，也可将s＝jω带入闭环特征方程，得到实部和虚部均为零的两个方程，将两个方程联立求解，即得根轨迹与虚轴交点的增益kg值与频率ω值。

如将s＝jω代入闭环特征方程，得到

1＋G(jω)H(jω)＝0

(4-19)

令上述方程的实部和虚部分别为零，有

Re[1＋G(jω)H(jω)]＝0

(4-20)

Im[1＋G(jω)H(jω)]＝0

(4-21)

利用这种实部方程和虚部方程，不难解出根轨迹与虚轴交点处的kg值和ω值。

【例4-6】设单位负反馈系统开环传递函数为G0(s)＝，试求根轨迹和虚轴的交点，并计算临界增益。

解:闭环系统特征方程为

s(s＋1)(s＋2)＋kg＝0

即

s3＋3s2＋2s＋kg＝0?

当kg＝kgp时，根轨迹和虚轴相交，令s＝jω代入，则特征方程为

(jω)3＋3(jω)2＋2(jω)＋kgp＝0kgp－3ω2＝0 2ω＋ω3＝0

将上式分解为实部和虚部，并分别等于零，即

解得

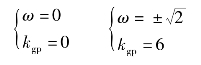
kgp＝0时，为根轨迹起点。kgp＝6时，根轨迹和虚轴相交，交点坐标为±kgp＝6为临界根轨迹增益。由此可以计算出临界开环增益为

也可利用劳斯判据确定kgp和ω值，可列出劳斯阵列表为

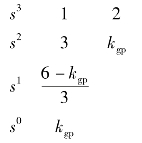
当劳斯阵列表中s1行等于0时，特征方程出现共轭虚根。令s1行等于0，则得

共轭虚根值可由s2行的辅助方程求得

即

【例4-7】已知单位负反馈系统开环传递函数为G0(s)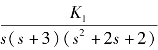＝　，试画出K1＝0→∞时的闭环系统的概略根轨迹。解:根据根轨迹绘制的基本法则，按步骤计算出各个有关参数，然后绘制根轨迹草图。

(1)n＝4，m＝0，有4条根轨迹。

(2)起始于开环极点p1＝0，p2＝－3，p3＝－1＋j，p4＝－1－j，终止于无穷远处。

(3)实轴上根轨迹为[－3，0]。

(4)n－m＝4，则有4条根轨迹趋于无穷远，它们的渐近线与实轴的交点和夹角为

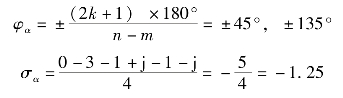
(5)分离点坐标d:

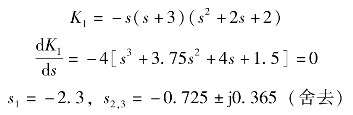
(6)根轨迹的出射角。由于开环传递函数没有零点，则只需计算出射角

θp3＝180°－∠(p3－p1)－∠(p3－p2)－∠(p3－p4)

＝180°－135°－26．6°－90°

＝－71．6°

根据对称性可得

θp4＝71．6°

(7)根轨迹与虚轴的交点。根据渐近线与实轴的夹角可知，一定有两条根轨迹通过虚轴。根据特征方程，用劳斯判据或令s＝jω的方法，可以求出与虚轴相交处的K1与ω值。系统特征方程为

s4＋5s3＋8s2＋6s＋K1＝0

列出相应的劳斯阵列表为1

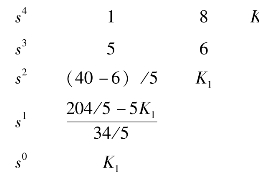
当劳斯阵列表中s1行等于0时，特征方程出现共轭虚根。令s1行等于0，则得

K1＝8．16

共轭虚根值可由s2行的辅助方程＋K1＝0求得

ω＝±1．1

即

s＝±j1．1

综上可得该系统的根轨迹如图4-13所示。

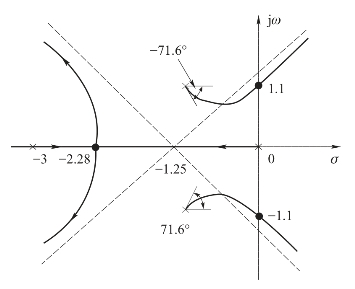
图4-13　例4-7的根轨迹图