一般控制系统的结构如图4-3所示。开环传递函数为

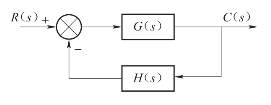
图4-3　一般控制系统结构图

G0(s)＝G(s)H(s)

(4-1)

闭环传递函数为

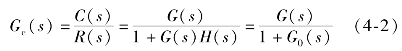
系统的开环传递函数以开环零、极点来表示时可以写为

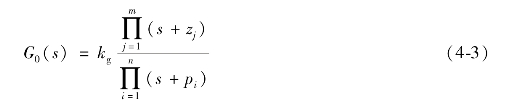
式中，s＝－zj，j＝1，2，…，m，为系统的开环零点；s＝－pi，i＝1，2，…，n，为系统的开环极点；kg为根轨迹增益，它与系统开环增益k0的关系为

根轨迹增益kg对应的开环传递函数，即式(4-3)称为首一型传递函数，而开环增益k0对应的开环传递函数

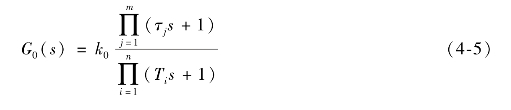
则称为尾一型传递函数。

由式(4-2)可得系统的闭环特征方程为

1＋G0(s)＝0(www.daowen.com)

(4-6)

用系统的开环传递函数G0(s)来表示，则有根轨迹方程

G0(s)＝－1

(4-7)

或

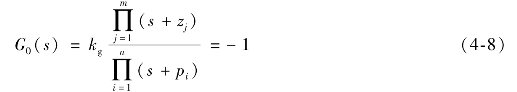
通过根轨迹的概念可知根轨迹上的每个点都满足闭环特征方程G0(s)＝－1的条件；反之，方程G0(s)＝－1的根必定在根轨迹上，所以把G0(s)＝－1叫作根轨迹的条件方程。

由于开环传递函数G0(s)是复变函数，分别要满足如下的幅值方程与相角方程

和

用零点和极点表示分别为

和

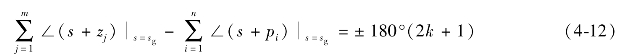
式(4-9)与式(4-10)的幅值方程与相角方程称为根轨迹的条件方程。也就是说，s平面上的任意点s＝sg如果满足根轨迹的幅值方程和相角方程，则该点在根轨迹上；复平面上的任意点s＝sg如果不满足根轨迹的幅值方程和相角方程，则复平面上的根轨迹不通过s＝sg。应当指出，幅值方程和相角方程是根轨迹上的点应该同时满足的两个条件，而相角条件是确定s平面上根轨迹的充分必要条件，也就是说，绘制根轨迹时，只需使用相角条件即可，当需要确定根轨迹上各点的kg值时才用幅值条件。