在MATLAB中，提供了求取连续系统的单位阶跃响应函数step，单位冲激响应函数impulse，零输入响应函数initial及任意输入下的仿真函数lsim。

【例3-12】已知典型二阶系统的传递函数为G(s)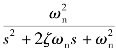＝　，其中ωn＝6，绘制系统在ζ＝0．1，0．3，0．5，0．7，0．9，1．0，2．0时的单位阶跃响应。

解:可执行如下程序

程序中利用step函数计算系统的阶跃响应，该程序执行后单位阶跃响应曲线如图3-20所示。从图中可以看出，在过阻尼和临界阻尼曲线中，临界阻尼响应具有最短的上升时间，响应速度最快；在欠阻尼的响应曲线中，阻尼系数越小，超调量越大，上升时间越短，通常取ζ＝0．4～0．8为宜。

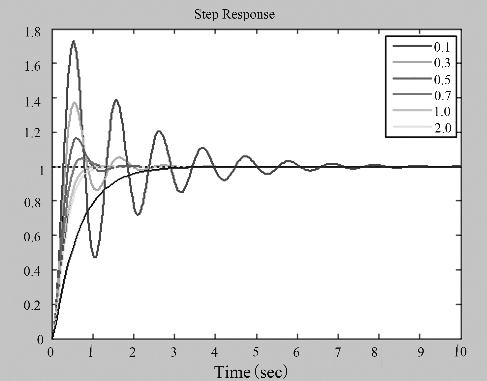
图3-20　例3-12系统的单位阶跃响应曲线

【例3-13】已知三阶系统的传递函数为G(s)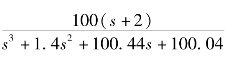＝　，试绘制系统的单位阶跃响应和单位脉冲响应曲线。(www.daowen.com)

解:可执行如下程序

运行结果如图3-21所示。

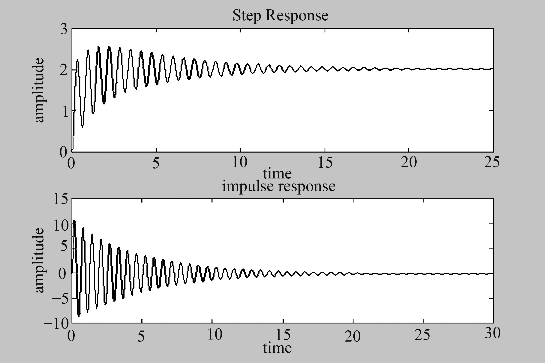
图3-21　例3-13系统的单位阶跃响应和单位脉冲响应曲线

【例3-14】如图3-22所示的Simulink的仿真框图可演示系统对典型信号的时间响应曲线，图中给出了阶跃响应曲线。

图3-22　Simulink的仿真框图和阶跃响应曲线