系统除有给定输入信号外，还承受扰动信号的作用。扰动信号破坏了系统输出和给定输入间的关系，因此干扰对输出的影响反映了系统的抗干扰能力。

以图3-16所示的典型恒值控制系统为例，系统总的稳态误差由两部分组成，一部分是给定量R(s)引起的误差，另一部分是扰动N(s)作用下的误差。即

E(s)＝ER(s)＋EN(s)

(3-66)

所以可以看出，扰动作用下系统的稳态误差就是系统在扰动作用下输出的负值，其表达式为

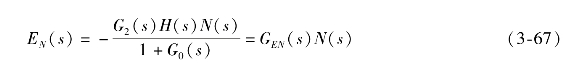
式中，G0(s)为系统开环传递函数。

扰动作用下系统的误差传递函数为

根据拉氏变换终值定理，求得扰动作用下的稳态误差为

由上式可知，系统扰动误差决定于系统的误差传递函数和扰动量。

【例3-10】如图3-18所示是典型工业过程控制系统的动态结构图。设被控对象的传递函数为Gp(s)＝　。求当采用比例调节器和比例－积分调节器时系统的稳态误差。(www.daowen.com)

图3-18　典型工业过程控制系统

解:(1)若采用比例调节器，即Gc(s)＝Kp。

由图3-18可以看出，系统对给定输入来说为Ⅰ型系统，令扰动N(s)＝0，给定输入R(s)＝R/s，则系统对阶跃给定输入的稳态误差为零。

若令R(s)＝0，N(s)＝N/s，则系统对阶跃扰动输入的稳态误差为

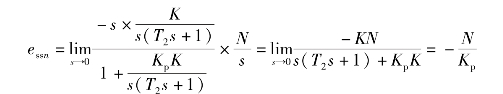
可见，阶跃扰动输入下系统的稳态误差为常值，它与阶跃信号的幅值成正比，与控制器比例系数Kp成反比。

(2)若采用比例－积分调节器，即Gc(s)＝Kp，这时控制系统对给定输入来说是Ⅱ型系统，因此给定输入为阶跃信号、斜率信号时，系统的稳定误差为零。

设R(s)＝0，N(s)＝N/s时

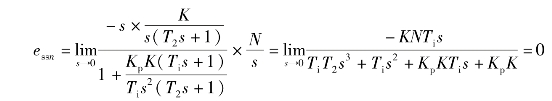
当R(s)＝0，N(s)＝N/s2时

可见，采用比例－积分调节器后，能够消除阶跃扰动作用下的稳态误差。其物理意义在于:因为调节器中包含积分环节，只要稳态误差不为零，调节器的输出必然继续增加，并力图减小这个误差。只有当稳态误差为零时，才能使调节器的输出与扰动信号大小相等而方向相反。这时，系统才进入新的平衡状态。在斜坡扰动作用下，由于扰动为斜坡函数，因此调节器必须有一个反向斜坡输出与之平衡，这样只有调节输入的误差信号为负常值才行。