控制系统的稳态性能一般是以阶跃、斜坡和抛物线信号作用在系统上产生的稳态误差来表征。下面分别讨论这三种不同输入信号作用于不同类型的系统时产生的稳态误差。
1.单位阶跃函数输入
当R(s)=1/s时,由式(3-58)得到稳态误差为
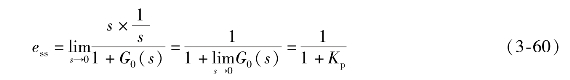
式中,![]() ,称为稳态位置误差系数,则
,称为稳态位置误差系数,则
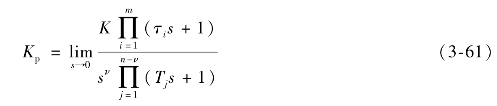
对0型系统,ν=0,Kp=K,ess=![]() ;
;
对Ⅰ型系统及Ⅰ型以上的系统,ν=1,2,…,∞,Kp=∞,ess=0。
由此可见,对于单位阶跃输入,只有0型系统有稳态误差,其大小与系统的开环增益成反比。而Ⅰ型和Ⅰ型以上的系统稳态位置误差系数均为无穷大,稳态误差均为零。
2.单位斜坡函数输入
当R(s)=1/s2时,系统稳态误差为
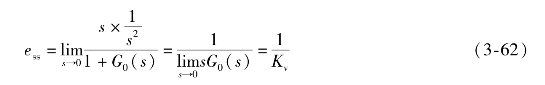
式中,Kv=![]() ,称为稳态速度误差系数。则
,称为稳态速度误差系数。则
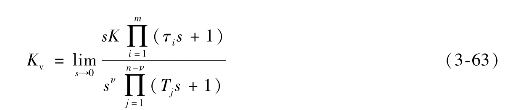
对0型系统,ν=0,Kv=0,ess=∞;
对Ⅰ型系统,ν=1,Kv=K,ess=![]() ;
;
对Ⅱ型或高于Ⅱ型系统,ν=2,3,…,∞,Kv=∞,ess=0。
由此可见,对于单位斜坡输入,0型系统稳态误差为无穷大;Ⅰ型系统可以跟踪输入信号,但有稳态误差,该误差与系统的开环增益成反比;Ⅱ型或高于Ⅱ型系统,稳态误差为零。
3.单位抛物线函数输入
当R(s)=1/s3时,系统的稳态误差为
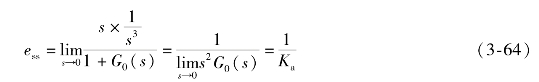
式中,Ka=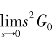 (s),称为稳态加速度误差系数。则
(s),称为稳态加速度误差系数。则
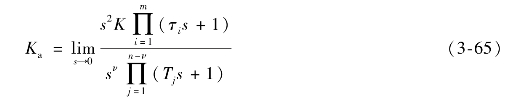 (www.daowen.com)
(www.daowen.com)
对0型系统,ν=0,Ka=0,ess=∞;
对Ⅰ型系统,ν=1,Ka=0,ess=∞;
对Ⅱ型系统,ν=2,Ka=K,ess=![]() ;
;
对Ⅲ型或高于Ⅲ型系统,ν=3,4,…,∞,Ka=∞,ess=0。
由此可知,0型及Ⅰ型系统都不能跟踪抛物线输入;Ⅱ型系统可以跟踪抛物线输入,但存在一定的误差,该误差与系统的开环增益成反比;只有Ⅲ型或高于Ⅲ型的系统,才能准确跟踪抛物线输入信号。
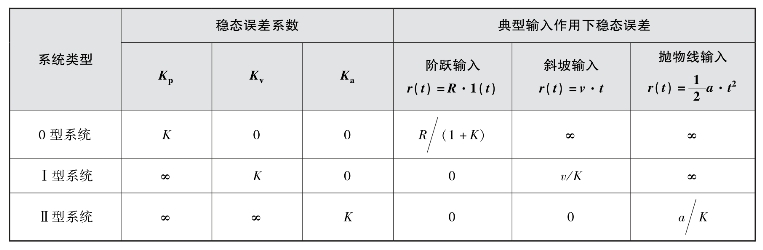
表3-1列出了不同类型的系统在不同参考输入下的稳态误差。
表3-1 稳态误差系数和稳态误差
【例3-9】已知单位反馈系统结构图如图3-17所示,输入信号r(t)=4+6t+3t2时,试求系统在r(t)作用下的稳态误差。
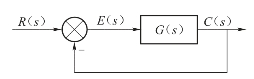
图3-17 例3-9系统结构图
(1)G(s)=![]() ;
;
(2)G(s)=![]() 。
。
解:(1)分析系统的开环结果,该系统为Ⅰ型系统,由于输入信号r(t)中含有加速度分量3t2,则要求系统至少Ⅱ型才能达到输出稳态响应与输入同步。故可直接得出结果,即ess=∞。
(2)按无差度写出开环传递函数的标准形式:
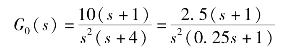
系统型号N=2,开环增益K=2.5。
计算静态误差:
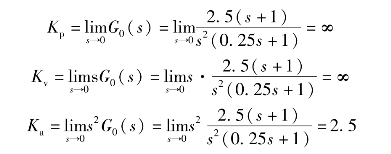
输入信号按单位典型输入关系写出,即
![]()
应用线性叠加原理得
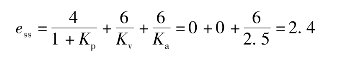
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








