设控制系统的典型动态结构如图3-16所示。

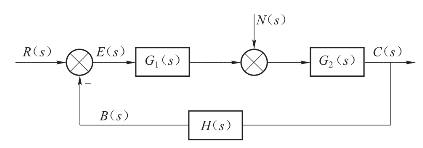
图3-16　控制系统的典型动态结构

设给定信号为r(t)，主反馈信号为b(t)，一般定义其差值e(t)为误差信号，即

e(t)＝r(t)－b(t)

(3-53)

当时间t→∞时，此值就是稳态误差，用ess表示，即

这种稳态误差的定义是从系统输入端定义的。这个误差在实际系统是可以测量的，因而具有一定的物理意义。

另一种定义误差的方法是由系统的输出端定义，系统输出量的实际值与期望值之差为稳态误差，这种方法定义的误差在实际系统中有时无法测量，因而只有数学上的意义。(www.daowen.com)

对于单位反馈系统，这两种定义是相同的。对于图3-16所示的系统，两种定义有如下的简单关系:

E(s)为从系统输入端定义的稳态误差，E′(s)为从系统输出端定义的稳态误差。本书以下均采用从系统输入端定义的稳态误差。

根据前一种定义，由图3-16可得系统的误差传递函数为

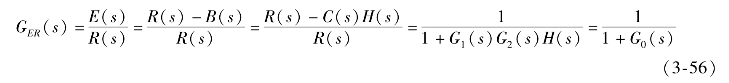
式中，G0(s)＝G1(s)G2(s)H(s)为系统开环传递函数。由此，误差的拉氏变换为

给定稳态误差为

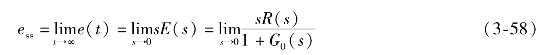
由此可见，有两个因素决定稳态误差，即系统的开环传递函数G0(s)和输入信号R(s)。系统的结构和参数不同，输入信号的形式和大小有差异，都会引起系统稳态误差的变化。下面就讨论这两个因素对稳态误差的影响。