由上述分析可知,二阶系统的单位阶跃响应,要达到既有充分的快速性,又有足够的阻尼使系统平稳,比较理想的选择是欠阻尼系统。因此,在工程实际中人们常常调整参数,使系统工作在欠阻尼状态。下面来进一步定量计算欠阻尼系统各项动态指标。
1.上升时间tr
根据定义,当t=tr时,c(tr)=1。由式(3-19),得

则
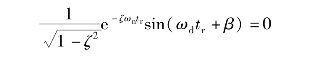
由于
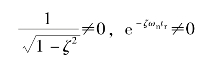
所以有
ωdtr+β=kπ, (k=1,2,…)
于是当k=1时,得上升时间
tr=(π-β)/ωd
(3-30)
显然,增大ωn或减小ζ,均能减小tr,从而加快系统的初始响应速度。
2.峰值时间tp
将式(3-19)对时间t求导,并令其为零,可求得峰值时间tp,即
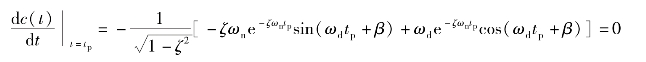
则
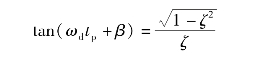
因为
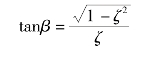
从而得
ωdtp=kπ (k=1,2,…)
按峰值时间定义,它对应最大超调量,即c(t)第一次出现峰值所对应的时间,所以tp应取

式(3-31)表明,峰值时间等于阻尼振荡周期(2π/ωd)的一半。当阻尼比ζ不变时,极点离实轴的距离越远,系统的峰值时间tp越短,或者说,极点离坐标原点的距离越远,系统的峰值时间越短。
3.超调量σ%
当t=tp时,c(t)有最大值c(t)max,即c(t)max=c(tp)。对于单位阶跃输入,系统的稳态值c(∞)=1,将峰值时间表达式(3-31)代入式(3-19),得最大输出为
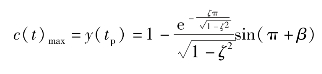
因为
![]()
所以
![]()
则超调量为
![]()
可见超调量仅由ζ决定,ζ越大,σ%越小,σ%和ζ的关系如图3-12所示。
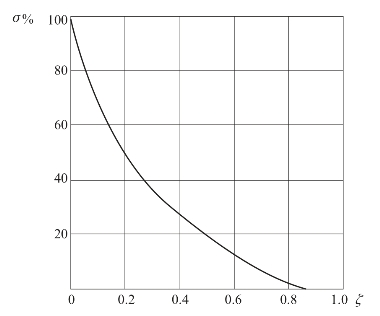
图3-12 欠阻尼二阶系统超调量和阻尼比的关系曲线(www.daowen.com)
4.调节时间ts
根据调节时间的定义,ts应由下式求出
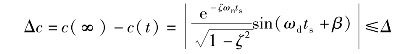
由上式可看出,求解上式十分困难。由于正弦函数存在,ts值与ζ间的函数关系是不连续的,为了简便起见,可采用近似的计算方法,忽略正弦函数的影响,认为指数函数衰减到Δ=0.05或Δ=0.02时,动态过程即结束。这样得到
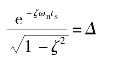
即
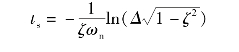
由此求得
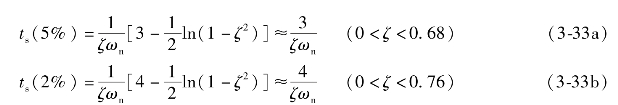
通过以上分析可知,ts近似与ζωn成反比。在设计系统时,ζ通常由要求的最大超调量决定,所以调节时间ts由无阻尼自然振荡频率ωn所决定。也就是说,在不改变超调量的条件下,通过改变ωn值来改变调节时间ts。
由以上讨论,可得到如下结论:
(1)阻尼比ζ是二阶系统的重要参数,由ζ值的大小,可以间接判断一个二阶系统的动态品质。在过阻尼的情况下,动态特性为单调变化曲线,没有超调量和振荡,但调节时间较长,系统反应迟缓。当ζ≤0时输出量做等幅振荡或发散振荡,系统不能稳定工作。
(2)一般情况下,系统在欠阻尼情况下工作。但是ζ过小,则超调量大,振荡次数多,调节时间长,动态特性品质差。应该注意,超调量只和阻尼比有关。因此,通常可以根据允许的超调量来选择阻尼比ζ。
(3)调节时间与系统阻尼比ζ和ωn这两个特征参数的乘积成反比。在阻尼比一定时,可通过改变ωn来改变动态响应的持续时间。ωn越大,系统的调节时间越短。
(4)为了限制超调量,并使调节时间ts较短,阻尼比一般在0.4~0.8,这时阶跃响应的超调量将在25%~1.5%。
【例3-1】已知系统结构如图3-13所示,试求单位阶跃响应的tr、tp、σ%、ts(Δ=2%)。
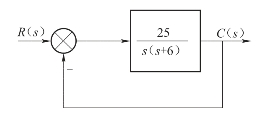
图3-13 例题3-1系统结构图
解:
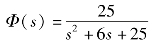
由标准式Φ(s)=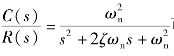 可得
可得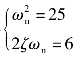
即
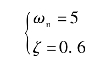
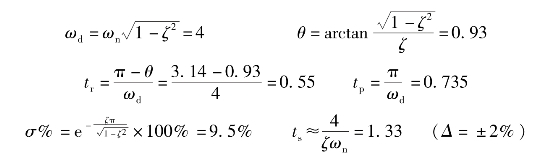
【例3-2】设单位反馈的二阶系统阶跃响应曲线如图3-14所示,试确定系统开环传递函数。
解:由图可直接得出系统的超调量为
![]()
峰值时间为
tp=0.1(s)
由式(3-31)及式(3-32)得
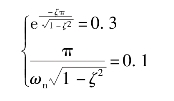
解得
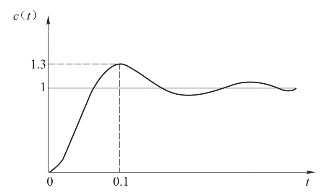
图3-14 例3-2响应曲线
ζ=0.357,ωn=3.36
于是得二阶系统开环传递函数为
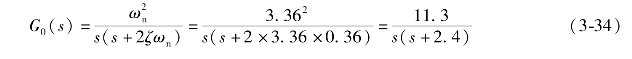
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







