在单位阶跃函数作用下,二阶系统输出的拉氏变换为
![]()
由于特征根s1,2与系统阻尼比有关,当阻尼比ζ为不同值时,单位阶跃响应有不同的形式,下面分几种情况来分析二阶系统的动态特性。
1.欠阻尼情况(0<ζ<1)
由于0<ζ<1,则系统的一对共轭复数根可写为
![]()
当输入信号为单位阶跃函数时,系统输出量的拉氏变换为

式中,ωd=ωn![]() ,称为阻尼振荡角频率,因此阻尼振荡周期为2π/ωd。对上式进行拉氏反变换,则欠阻尼二阶系统的单位阶跃响应为
,称为阻尼振荡角频率,因此阻尼振荡周期为2π/ωd。对上式进行拉氏反变换,则欠阻尼二阶系统的单位阶跃响应为
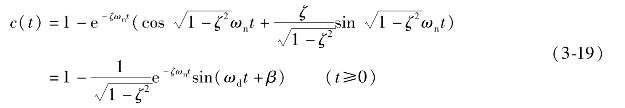
式中,sinβ=![]() ,cosβ=ζ,则有
,cosβ=ζ,则有

由式(3-19)知欠阻尼二阶系统的单位阶跃响应由两部分组成,第一项为稳态分量,第二项为动态分量。它是一个幅值按指数规律衰减的有阻尼的正弦振荡系统,振荡角频率为ωd。其响应曲线如图3-11所示。
2.临界阻尼情况(ζ=1)
当ζ=1时,系统有两个相等的负实根,为
s1,2=ωn
(3-21)
在单位阶跃函数作用下,输出量的拉氏变换为
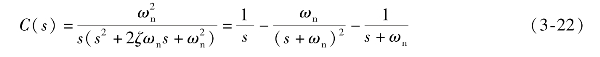
其反拉氏变换为
c(t)=1-e-ωnt(1+ωnt) (t≥0)
(3-23)(www.daowen.com)
式(3-23)表明,临界阻尼二阶系统的单位阶跃响应是稳态值为1的非周期上升过程,整个响应特性不产生振荡,此时响应曲线如图3-11所示。
3.过阻尼情况(ζ>1)
当ζ>1时,系统有两个不相等的负实根
![]()
当输入信号为单位阶跃函数时,输出量的拉氏变换为

其拉氏反变换为
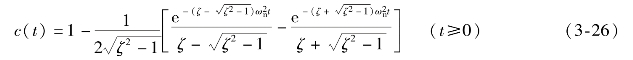
上式表明,系统响应含有两个单调衰减的指数项,它们的代数和决不会超过稳态值1,因而过阻尼二阶系统的单位阶跃响应是非振荡的。其响应曲线如图3-11所示。
4.无阻尼情况(ζ=0)
当ζ=0时输出量的拉氏变换为

其特征方程式的根为
s1,2= -jωn
(3-28)
因此二阶系统的输出响应为
c(t)=1-cosωnt (t≥0)
(3-29)
式(3-29)表明,系统为不衰减的振荡,其振荡频率为ωn,系统属不稳定系统。其响应曲线如图3-11所示。
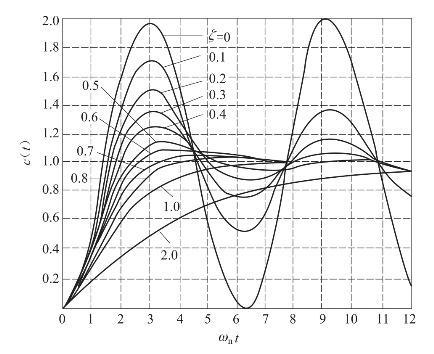
图3-11 阻尼比不同时二阶系统单位阶跃响应曲线
阻尼比ζ为二阶系统的重要特征参量,由图3-11可以看出,在不同阻尼比ζ时,二阶系统的动态响应有很大区别。当ζ=0时,系统不能正常工作,而在ζ>1时,系统动态响应进行得太慢,所以,对二阶系统来说,欠阻尼情况是最有意义的,下面将以欠阻尼情况讨论动态特性指标。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






