1.多项式形式的传递函数表示

若控制系统传递函数表示为G(s)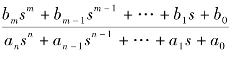＝(n≥m)的形式，则在MATLAB软件中进行表示时，用到了多项式的表示方法。

首先，将传递函数分子、分母多项式按降幂排列，构成两个向量num和den。分子多项式变量num＝[bm，bm－1，…，b1，b0]，分母多项式变量den＝[an，an－1，…，a1，a0]，然后用函数tf()建立传递函数的模型，调用格式:

sys＝tf(num，den)

【例2-14】若系统传递函数为G(s)＝，试用MATLAB建立其传递函数模型。

解:在MATLAB的命令行提示符“＞＞”下输入

回车后屏幕显示:

注意:每行语句后用“；”，表示该行命令的运算结果不显示出来；每个变量的不同元素间可以用“，”，也可以用空格相分隔；函数的各个变量之间一定用“，”相分隔。

2.零极点形式的传递函数表示

若控制系统传递函数表示为G(s)＝K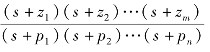(n≥m)的零极点形式，则在MATLAB中可将传递函数表示为零点向量、极点向量和增益向量的形式。零点向量z＝[－z1，　－z2…，　－zm]、极点向量p＝[－p1，　－p2…，　－pn]和增益向量k＝[K]。然后用函数zpk()建立系统的数学模型，调用格式为:

sys＝zpk(z，p，k)

【例2-15】若系统传递函数为G(s)＝　，试用MATLAB建立其传递函数模型。(www.daowen.com)

解:在MATLAB的命令行提示符“＞＞”下输入:

回车后屏幕显示:

说明:“z＝[]”表示z向量是个空矩阵，没有元素，不等同于“z＝[0]”。

3.因式乘积形式的传递函数表示

若控制系统的传递函数是因式乘积的形式，但不是显式的零极点形式，还可以用如下方式建立系统的数学模型。

【例2-16】若系统传递函数为G(s)＝　，试用MATLAB建立其传递函数模型。

解:在MATLAB的命令行提示符“＞＞”下输入

回车后屏幕显示:

函数conv(a，b)表示两个变量的卷积，也可以表示两个向量a和b构成的多项式的乘积。若多项式(s2＋2s＋4)(3s＋2)(s＋5)可以用如下语句表示num1＝conv(conv([1 2 4]，[3 2])，[1 5])或conv([1 2 4]，conv([3 2]，[1 5]))。运行结果为:

num1＝3　　23　　56　　88　　40