根据图2-18求出系统的传递函数，涉及动态结构图的化简问题。结构图化简需要遵循一定的基本原则，也就是要保证化简前后的代数等价关系不变，即满足动态结构图在变换前后要保持等效，把这种对结构图的化简原则称为等效变换原则。

1.串联连接的化简

串联连接系统的结构图如图2-19所示，串联连接是各个环节首尾相连。

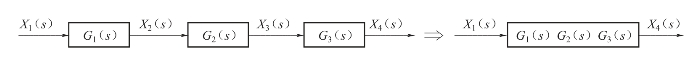
图2-19　串联连接的化简

由传递函数的定义有串联系统总的传递函数为

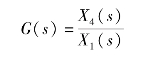
做简单变形如下

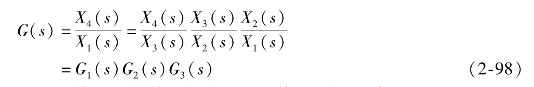
可见，若干个串联环节组成的系统的传递函数等于各串联环节传递函数的乘积。

2.并联连接的化简

并联连接系统的结构图如图2-20所示。并联连接的各环节输入均等于系统总的输入，各环节输出的代数和等于系统总的输出。

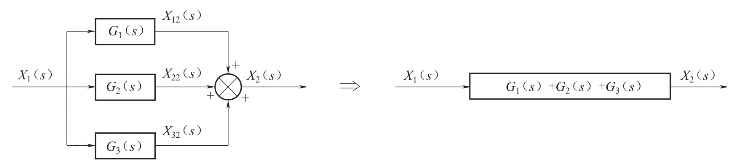
图2-20　并联连接的化简

由传递函数的定义有并联系统总的传递函数为

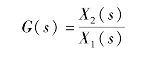
做简单变形如下

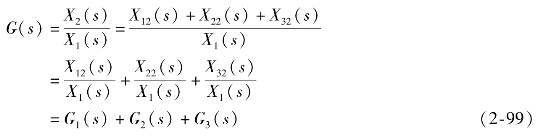
并联环节的传递函数等于各并联环节传递函数的代数和。

3.反馈连接

反馈连接系统结构图如图2-21所示，由于加了一个反馈回路而构成了闭环系统。

图2-21　反馈回路化简

由传递函数的定义可以有

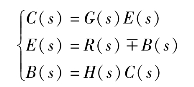
联立求解，消去E(s)、B(s)，得到系统的传递函数为

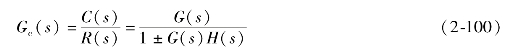
式中，正号为负反馈，负号为正反馈。可见，反馈连接系统的传递函数是一个分式，分子是前向通路的传递函数，分母是1和前向通路传递函数与反馈通路传递函数乘积的代数和。

对于反馈回路，把Gc(s)＝　称为闭环系统的传递函数。相对地，把Go(s)＝G(s)H(s)称为闭环系统的开环传递函数，即从反馈环节末端断开系统时，前向通路传递函数G(s)和反馈通路传递函数H(s)的乘积。

说明:对于负反馈系统，当开环传递函数G(s)H(s)＞0时，闭环传递函数的分母大于1，则Gc(s)＜G(s)，相当于系统由开环构成闭环后，增益变小；当G(s)H(s)＜0时，闭环传递函数的分母小于1，系统由开环构成闭环后，增益变大；当G(s)H(s)＝－1时，Gc(s)＝∞，即无论原开环系统如何，构成闭环后系统将失去稳定输出。因而，有人把反馈看作一把“双刃剑”，它既可以使原开环系统变成精确跟踪输入目标的稳定系统，也可以使系统永远失去稳定性。所以应用反馈控制时要加以注意。

4.相加点(综合点)移动

相加点的移动，也就是将位于方框输入端(或者输出端)的相加点移动到方框的输出端(或者输入端)，跨越中间环节的传递函数，其移动不外乎有逆着信号方向移动(逆移)、顺着信号方向移动(顺移)和两个相邻的相加点位置的互换三种形式。各种移动的原则就是保证移动前后系统要保持等效。各规则如图2-22、图2-23和图2-24所示。

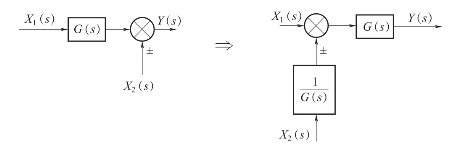
图2-22　相加点逆移(www.daowen.com)

图2-23　相加点顺移

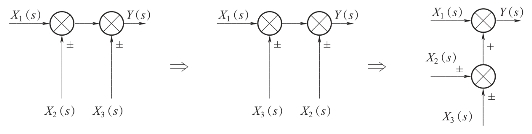
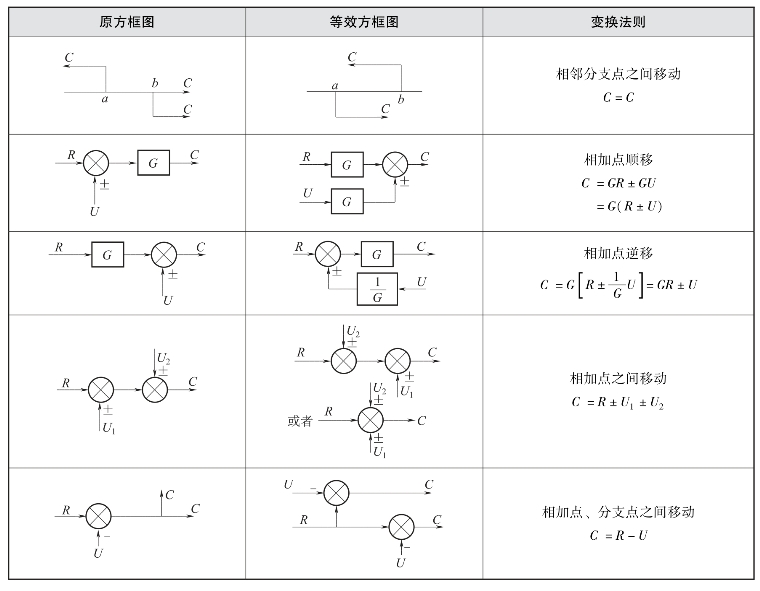
图2-24　相加点互换

从以上结构图的分析可以看出，相加点逆移时，为保证等效，应在移动支路中除以跨越的传递函数；相加点顺移时，为保证等效应在移动支路中乘以跨越的传递函数；两个相邻的相加点，中间不跨越环节时，其位置可以互换。

5.分支点(分离点)移动

分支点的移动，也是将位于方框输入端(或者输出端)的分支点移动到方框的输出端(或者输入端)，跨越中间环节的传递函数，其移动也有逆着信号方向移动(逆移)和顺着信号方向移动(顺移)两种形式，各种移动同样遵循等效变换原则。各规则如图2-25和图2-26所示。

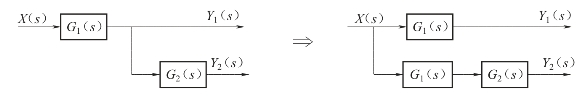
图2-25　分支点逆移

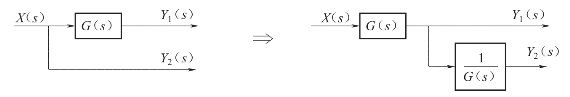
图2-26　分支点顺移

可见，分支点逆移时，为保证等效应在移动支路中乘以跨越的传递函数；分支点顺移时，为保证等效应在移动支路中除以跨越的传递函数。

结合相加点的移动规则，为了方便记忆，不妨记忆其中的任意三个字:如“加顺乘”“加逆除”“分顺除”　“分逆乘”。　“加”和“分”相对，　“顺”和“逆”相对，　“乘”和“除”相对。三字中有且仅有两个字同时变化。

注意:相加点与分支点之间没有简单互换法则。

【例2-12】多回路系统的传递函数如图2-27(a)所示，试采用结构图等效变换法则化简结构图。

解:由结构图可见，该图有三层反馈，所以可以从最内部的反馈回路开始逐步化简。

第一步:合并内部回路中的串联环节，如图2-27(b)所示。

第二步:合并内部回路中的并联环节，如图2-27(c)所示。

第三步:合并内部回路中的反馈环节，如图2-27(d)所示。

第四步:继续合并回路中的串联环节，如图2-27(e)所示。

第五步:继续合并回路中的反馈环节，如图2-27(f)所示。

所以，得到该系统的传递函数为

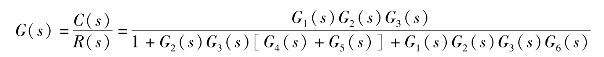
几种基本的结构图等效变换法则列于表2-3中。

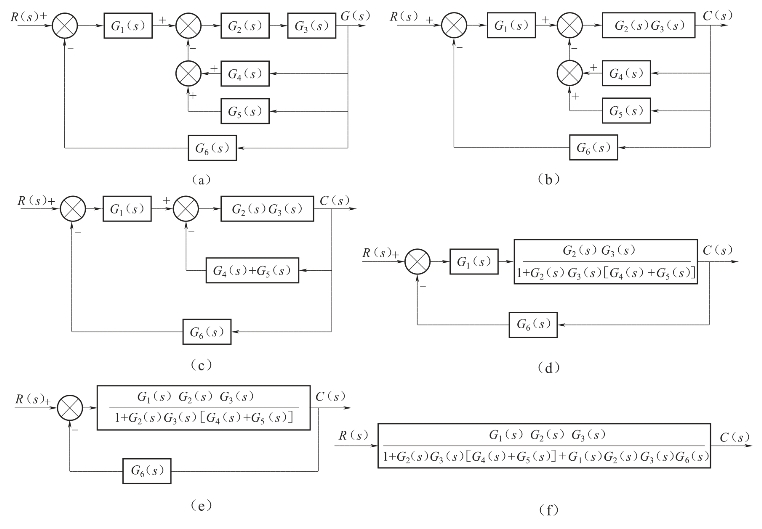
图2-27　系统结构图及化简过程示意图

表2-3　结构图等效变换法则

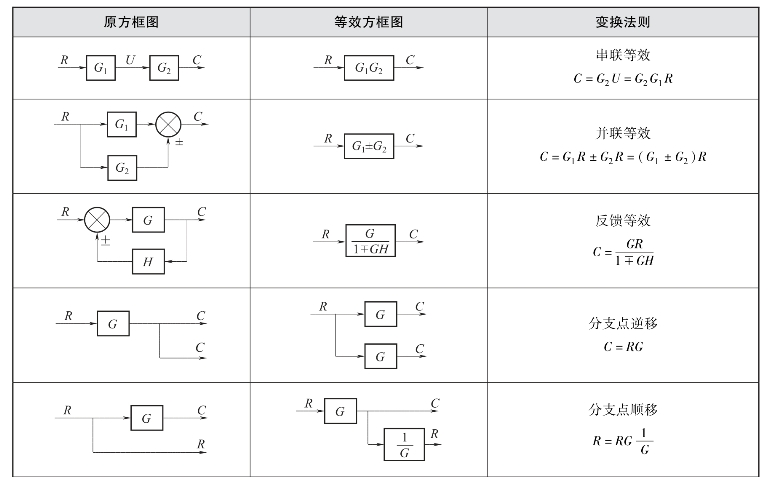
续表

掌握了上述几种结构图等效变换法则后，对于一般的结构图都能等效地变成串、并联和反馈连接三种典型的连接形式，求出其传递函数。但是，有时更复杂的结构图，只用等效变换法则还不能简化，例如，在结构图中有相加点、分支点相间存在的，为了简化结构图就要使它们之间互相移位，但仍然遵循变换后信号传递关系不变的原则，如图2-28(a)所示。相加点、分支点在图中的位置是相间存在的，若变成典型结构连接，用前面介绍的几种原则都不适用，只能首先根据信号传递关系，将结构图重新排列，变相加点、分支点相间为相邻，从而达到简化目的，如图2-28(b)所示。这里就没有统一的规则可用了，只能具体问题具体分析。

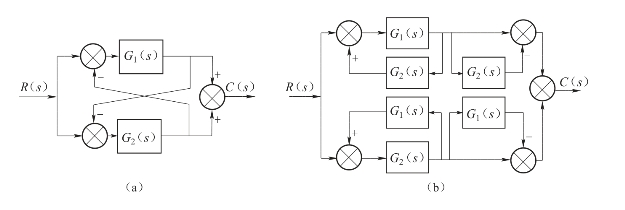
图2-28　相加点和分支点之间移位的等效变换