1.动态结构图的组成

动态结构图又称方框图(Block Diagram)、结构图，是一种网络拓扑约束下的有向线图。控制系统的动态结构图一般由以下几部分组成。

①有向线段:带有箭头的线段，表示信号的传递方向，线段上标注信号的原函数或象函数，如图2-14(a)所示。

②方框:方框中为元部件的传递函数，如图2-14(b)所示。

③分支点(分离点):表示信号分支或引出位置，从同一点引出的信号完全相同，如图2-14(c)所示。

④相加点(综合点):对两个及以上信号进行代数和运算，“＋”号表示相加，“－”号表示相减，如图2-14(d)所示。

2.系统动态结构图的建立

图2-14　组成动态结构图的基本单元

把组成系统的每一个环节用一个方框表示，方框内写上该环节的传递函数，然后把这些方框按照实际系统的信号流通关系连接起来，用箭头标出信号的传递方向，就构成了系统的动态结构图。

【例2-10】画出图2-15所示简单RC网络的动态结构图。

解:(1)列写各元件的原始方程式

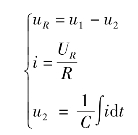
(2)取拉普拉斯变换，在零初始条件下，表示成方框形式(因果关系)。

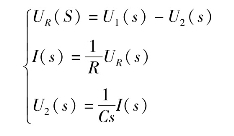(www.daowen.com)

(3)将这些方框依次连接起来得到图2-16。

图2-15　RC网络

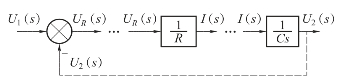
图2-16　RC网络的结构图

【例2-11】已知两级RC网络如图2-17所示，画出该系统的动态结构图。

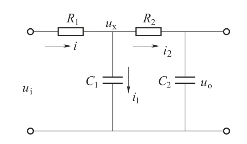
图2-17　两级RC网络电路图

解:设一个中间变量为电容C1的电压ux，采用复数阻抗法顺序写出各算子代数方程和绘出相应的方框图如下

将各基本环节的方块按照信号流通方向连接起来就可以得到如图2-18所示的系统结构图。至于系统总的传递函数G(s)＝，可以联立化简上述代数方程组得到，也可以在结构图上直接通过结构图化简得到。

图2-18　两级RC网络系统结构图