1.线性定理

若函数f1(t)、f2(t)的拉氏变换分别为F1(s)、F2(s)，则

L[af1(t)＋bf2(t)]＝aF1(s)＋bF2(s)

(2-59)

2.延迟定理

若函数f(t)的拉氏变换为F(s)，则

L[f(t－τ)]＝e－τsF(s)

(2-60)

信号f(t)与它在时间轴上的平移信号f(t－τ)的关系如图2-12所示。

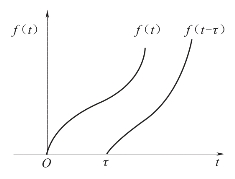
图2-12　信号的时间延迟示意图

延迟定理说明了时间域的平移变换对应于复数域的衰减变换，应用该定理，可以简化一些信号的拉氏变换的求取。

3.衰减定理

若函数f(t)的拉氏变换为F(s)，则

L[e－αtf(t)]＝F(s＋α)

(2-61)

该定理说明了时间信号f(t)在时间域的衰减对应于复频域的负延迟。

【例2-9】试求时间函数f(t)＝e－αtsinωt的拉氏变换。

解:因为正弦函数的拉氏变换为

所以，应用拉氏变换的衰减定理可以直接写出

衰减定理与延迟定理表明了时间域与复频域的对偶关系。

4.微分定理

若函数f(t)的拉氏变换为F(s)，且f(t)的各阶导数存在，则f(t)各阶导数的拉氏变换为

当所有的初值(各阶导数的初值)均为零时，即

f(0)＝f′(0)＝…＝f(n－1)(0)＝0

则

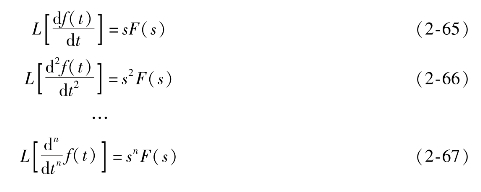(www.daowen.com)

5.积分定理

若函数f(t)的拉氏变换为F(s)，则

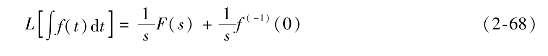
式中

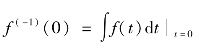
为函数f(t)在t＝0时刻的积分值。

6.初值定理

若函数f(t)的拉氏变换为F(s)，且在t＝0＋处有初值f(0＋)，则

可见，时域函数的初值对应于复频域内的终值。

7.终值定理

若函数f(t)的拉氏变换为F(s)，且f(∞)存在，则

即时域函数的终值对应于复频域内的初值。

8.卷积定理

若时域函数f1(t)、f2(t)分别有拉氏变换F1(s)、F2(s)，时域函数的卷积积分为

又常表示为

f1(t)*f2(t)

(2-72)

则其拉氏变换为

这表明时域函数的卷积积分运算对应于复频域函数的乘积运算。证明可参考其他文献。

时域函数经过拉氏变换在复频域中表示有两个优点:一个是简化了函数，例如指数函数和正、余弦函数都是时域中的超越函数，在复频域中成为了有理函数；另一个是简化了运算，如时域函数的卷积积分运算成为复频域中函数的乘积运算，时域中的微分、积分运算成为复频域内的代数运算等。

常用的拉氏变换基本定理可以参见表2-2。

表2-2　拉普拉斯变换基本定理表

续表

拉氏变换是将时域函数f(t)变换为复变函数F(s)，相应地它的逆运算可以将复变函数F(s)变换回原时域函数f(t)。拉氏变换的逆运算称为拉普拉斯反变换，简称拉氏反变换。