我们推导元件或系统的微分方程时，假定它们都是线性的，所得到的微分方程是线性微分方程。但是在工程实际中，纯粹的线性系统是不存在的，因为组成系统的元件都存在程度不同的非线性特性。在控制理论中，按特性的非线性程度不同把它们分成两类。第一类是非线性特性在指定工作点附近不存在饱和、继电、死区、滞环等现象，把这种非线性特性叫作非本质非线性特性；第二类是非线性特性在指定工作点附近存在饱和、继电、死区、滞环等现象，这种非线性特性叫作本质非线性特性，如图2-9所示。如果系统所含非线性特性是本质非线性特性，要用非线性系统的理论来研究。如果系统所含的非线性特性是非本质非线性特性的，经过线性化后，仍可用线性系统理论进行研究。

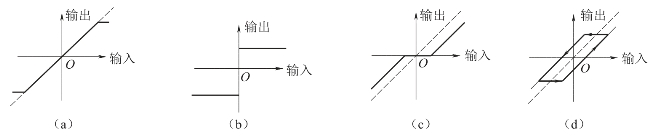
图2-9　非线性特性曲线

(a)饱和；(b)继电；(c)死区；(d)滞环

非线性特性的线性化就是在工作点附近的小范围内，把非线性特性用线性特性来代替的过程。线性化的基本条件是非线性特性必须是非本质的；其次，系统各变量对于工作点仅有微小的偏移。这些条件对绝大多数控制系统来说是能够满足的，因为实际系统大多工作在小偏差的情况下。

非线性系统线性化的步骤如下:

(1)确定系统输入－输出之间的函数关系y(x)。

(2)在工作点x0邻域将y(x)展开为泰勒级数，即

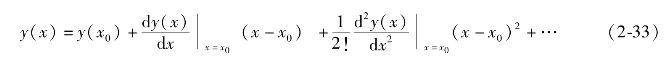
(3)当(x－x0)很小时，可略去二阶以上的高次项得到

(4)(x－x0)很小时，有y(x)－y(x0)很小，可写出增量式为

Δx＝x－x0

Δy＝y(x)－y(x0)

令

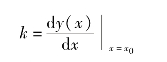
即在工作点x0邻域，将曲线斜率视为常数，写成增量方程为

Δy＝kΔx

(2-35)

将增量以普通变量来表示，就得到了线性化方程

y＝kx

(2-36)

线性化的图形求法:若非线性特性是非本质非线性，况且在工作点附近仅有微小的偏移，则在该工作点邻域用该点的切线代替曲线进行系统分析的方法，就是非线性特性的图形法。

【例2-7】已知非线性函数为

y＝sinθ

(2-37)

试分别在θ0＝0及θ0＝π两点领域对函数进行线性化处理。

解:按一元函数的泰勒展开式对正弦函数展开为

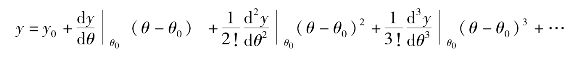
写成偏量方程为

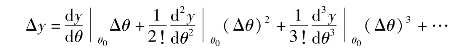
即

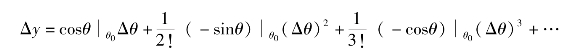
在θ0＝0的领域有

忽略Δθ二次以上高次项，得一次项近似式为

Δy＝Δθ

上式说明，在θ0＝0的领域，正弦函数值与相角的值近似相等，即

y≈θ(www.daowen.com)

在θ0＝π的领域有

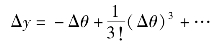
同理，一次近似式为

(2-38)

Δy＝－Δθ

故在θ0＝π的领域，正弦函数线性化系数k＝－1，即

y≈－θ

(2-39)

可见，在不同的工作点，线性方程的系数是不同的，这是由于各点处切线斜率不同。其线性化关系如图2-10所示。

【例2-8】整流晶闸管工作原理示意图如图2-11(a)

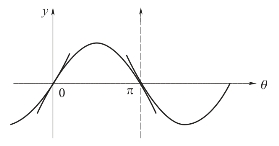
　图2-10　正弦函数线性化

所示，其输入量为控制角α，输出量为整流电压UD，试建立其线性化模型。

解:由电子技术可知，整流电压UD与控制角α之间的关系为

UD＝U0cosα

(2-40)

式中，U0表示理想空载整流电压值(V)。

其特性曲线如图2-11(b)所示，很显然是非线性关系。设调速系统的工作点为(α0，UD0)，写出如式(2-35)的增量方程为

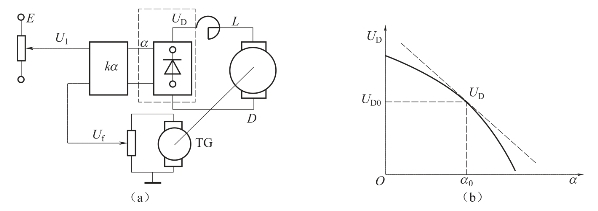
图2-11　整流晶闸管工作原理电路及其特性曲线

(a)工作原理电路；(b)特性曲线

UD－UD0＝k(α－α0)

(2-41)

由于

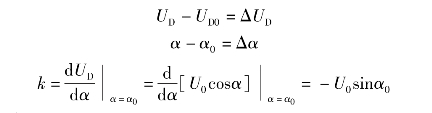
所以线性化增量方程为

ΔUD＝kΔα

以普通变量来表示增量，写成线性化方程为

(2-42)

UD＝kα

(2-43)

将非线性特性线性化时，有以下几点需要注意:

(1)本质非线性系统不可以进行线性化正是因为这类非线性系统的不连续性、不可导性使得其泰勒级数展开式在工作点邻域的切线近似不成立，因此对于本质非线性系统，另外采用第7章所叙述的方法来进行分析。

(2)对于多变量情况，其线性化方法相似。如双变量时，函数关系可以表示为f(x，y)，如果满足在工作点邻域的连续、可导条件，线性化原理与前面所述相同，即在工作点(x0，y0，Δf(x0，y0))处的增量表达式为

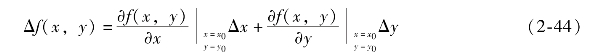
再经过变量一般化即可。

(3)工作点不同时，其线性化系数也是不同的，因此其线性化方程也是不同的。这一点表现在非线性函数关系上就是在不同的工作点，可以获得斜率不同的切线，所以线性化系数是各异的。因此非线性系统线性化时，一定要先确定其工作点，这样求得的线性化方程才是正确的。

(4)非线性系统在工作点邻域的线性化方程，应满足其函数关系的变化是小范围的，否则，误差将会很大。线性化方程是增量方程以变量来表示，所以当增量范围过大时，不满足线性化条件。