1.RLC电学系统

电学系统中，一般所需遵循的是元件约束和网络约束。元件约束指电阻、电容、电感等器件的电压－电流关系遵循广义欧姆定律；网络约束指基尔霍夫电压定律和基尔霍夫电流定律。

【例2-1】RLC无源网络如图2-1所示，图中R、L、C分别为电阻(Ω)、电感(H)、电容(F)，建立输入电压ui(t)和输出电压uo(t)之间的微分方程。

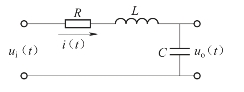
图2-1　RLC无源网络

解:根据电路理论中的基尔霍夫定律，可得

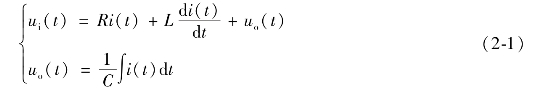
消去中间变量i(t)，则

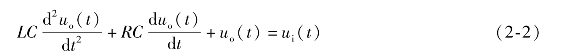
令LC＝T 2，RC＝2ζT，则上式又可以写成如下形式

式中，T称为时间常数，单位为秒；ζ称为阻尼系数，无量纲。

式(2-2)和式(2-3)就是所求的RLC网络的二阶微分方程。

2.运算放大器电路系统

与电阻、电感、电容这些无源元件相反，凡是能够把外部能量传送到系统中去的物理元件称为有源元件。线性集成电路运算放大器就是其中之一，因为它含有电源并能将电源的能量传送到系统中去。运算放大器(简称运放)的开环放大倍数很高(达104～108)，经运算放大器反相输入端流入放大器的电流很小，可以近似为零，所以运算放大器的反相输入端可以视为“虚地”点。

运算放大器性能稳定，工作可靠，调整方便，在控制系统中广泛用作放大元件，或与电阻、电容一起构成校正装置，形成各种类型的调节器。

另外，运算放大器的输入阻抗很高，输出阻抗很低，在控制系统中常位于输入端，当其带上负载时，负载对输出电压的影响(即负载效应)很小，可以忽略不计。

【例2-2】如图2-2所示为运算放大器有源网络，图2-2(a)为比例型(P型)运算放大器网络，图2-2(b)为积分型(I型)运算放大器网络，图2-2(c)为微分型(D型)运算放大器网络，图2-2(d)、(e)、(f)分别为比例-积分型(PI型)、比例-微分型(PD型)、比例-积分-微分型(PID型)运算放大器网络的电路图，试求各自的微分方程。

解:(a)根据运算放大器反相输入端为“虚地”的特点，有i3≈0，i1≈i2，则有

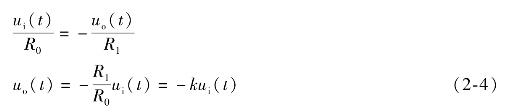
由于输入ui(t)和输出变量uo(t)之间成比例关系，所以此电路称为比例(Proportional)型运算放大器，简称P型运放。k称为放大倍数(或增益)，它等于运算放大器反馈回路阻抗与输入回路阻抗之比。

图2-2　运算放大器有源网络

(a)P型；(b)I型；(c)D型；(d)PI型；(e)PD型；(f)PID型

(b)由i1＝i2，有

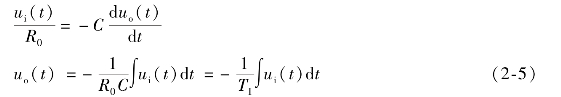
由于输入ui(t)和输出变量uo(t)之间成积分关系，所以此电路称为积分(Integral)型运算放大器，简称I型运放。TI称为时间常数。

(c)由i1＝i2，有

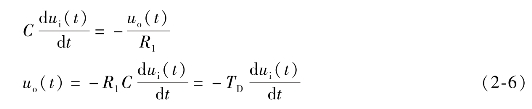
由于输入ui(t)和输出变量uo(t)之间成微分关系，所以此电路称为微分(Differential)型运算放大器，简称D型运放。TD为时间常数。

同理可得PI型、PD型和PID型运算放大器的微分方程，它们分别为:

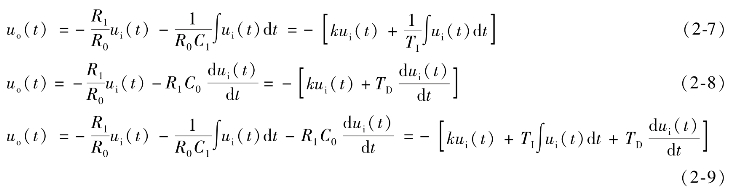
说明:运算放大器输入与输出之间成反相关系，一般为了方便，分析时可以不考虑负号的影响，即微分方程中都不写“－”号。

3.机械旋转系统

【例2-3】已知机械旋转系统如图2-3所示，试列出作用力矩Ms(t)为输入量、角速度ω(t)为输出量的系统运动方程。

解:由角加速度方程

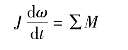
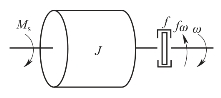
图2-3　机械旋转系统

其中，J表示转动惯量；ω表示旋转角速度；∑M表示和力矩。则

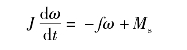
其中，Ms表示作用力矩；　－fω表示阻尼力矩，其大小与角速度成正比，负号表示其方向与作用力矩方向相反。整理得

式(2-10)即是输入变量作用力矩Ms(t)与输出变量旋转角速度ω(t)的运动方程，是一个一阶微分方程。

若以角位移θ(t)为输出变量，因为

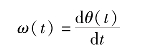
代入式(2-10)得

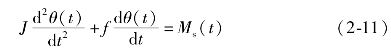
式(2-11)即为以转角θ(t)为输出变量，以作用力矩Ms(t)为输入变量的二阶微分方程。

4.弹簧阻尼系统

【例2-4】如图2-4所示为一弹簧阻尼系统，当外力F(t)作用于系统时，系统将产生运动。试列写外力F(t)与位移y(t)之间的微分方程。

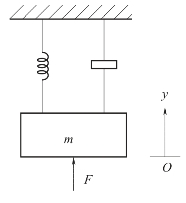
图2-4　弹簧阻尼系统(www.daowen.com)

解:弹簧和阻尼器有相应的弹簧阻力F1(t)和黏性摩擦力

F2(t)，根据牛顿第二定律有

F1(t)和F2(t)可由弹簧、阻尼器特性写出为

式中，k为弹簧系数；f为阻尼系数。

将式(2-13)代入式(2-12)得

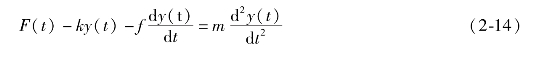
整理且标准化得

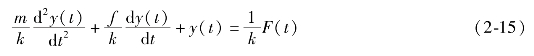
令T＝为时间常数；ζ＝为阻尼比；K＝为放大系数。则式(2-15)可写成如下形式

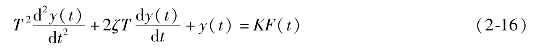
5.电枢控制的直流电动机系统

【例2-5】已知直流电动机定子与转子的电磁关系如图2-5所示，机电系统原理如图2-6所示，试写出其运动方程。

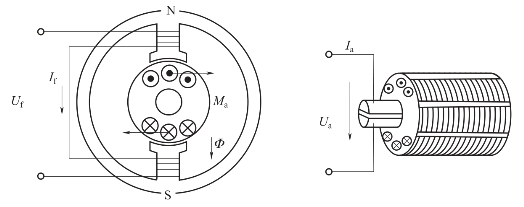
图2-5　电动机定、转子电磁关系示意图

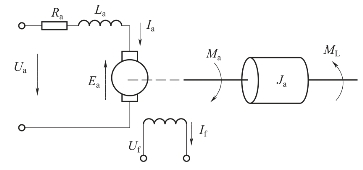
图2-6　直流电动机机电系统原理

解:直流电动机的运动是一复合系统的运动。它由两个子系统构成，一个是电网络系统，由电网络得到电能，产生电磁转矩；另一个是机械运动系统，输出机械能带动负载转动。在图2-5的电动机结构示意图中，设主磁通Φ为恒定磁通，也就是说在励磁电压Uf为常数时，产生常数值的励磁电流If，从而主磁通Φ也为常数。忽略旋转黏滞系数fa，则可以写出各平衡方程如下。(有关直流电动机的详细内容，可以参阅电力拖动有关书籍)

(1)电网络平衡方程为

式中，Ua表示电动机的电枢电压(V)；Ia表示电动机的电枢电流(A)；Ra表示电枢绕组的电阻(Ω)；La表示电枢绕组的电感(H)；Ea表示电枢绕组的感应电动势(V)。

(2)电动势方程为

Ea＝Ceω　(2-18)

式中，ω表示电枢旋转角速度(rad/s)；Ce表示电动势常数(V·s/rad)，由电动机的结构参数确定。

(3)机械转矩平衡方程为

式中，Ja表示电动机转子的转动惯量(N·m·s2/rad)；Ma表示电动机的电磁转矩(N·m)；ML表示折合阻力矩(N·m)。

(4)电磁转矩方程为

Ma＝CmIa

(2-20)

式中，Cm表示电磁转矩常数(N·m/A)，由电动机的结构参数确定。

将式(2-17)～式(2-20)联立得方程组如下

消去中间变量Ia、Ea、Ma，得到输入为电枢电压Ua(t)，输出为转轴角速度ω(t)的二阶微分方程

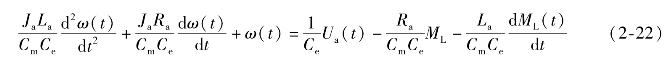
令TM＝，为电枢回路机电时间常数；Ta，为电磁时间常数。则

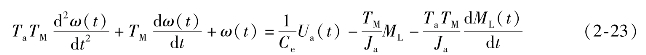
为电枢控制的直流电动机的运动方程，是一个二阶线性微分方程。

式(2-23)还表明，电枢控制的直流电动机有两个输入，一个是控制作用电枢电压Ua(t)，一个是扰动因素负载转矩Mf(t)。因为直流电动机是线性元件，满足叠加原理，当只讨论Ua(t)与ω(t)的关系时，可认为Mf(t)＝0。则直流电动机的微分方程可写为

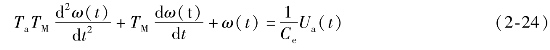
因为直流电动机电枢绕组的电感一般都很小，如果略去电枢绕组的电感La，即Ta＝0，则可以得到一阶线性微分方程

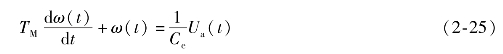
6.测速发电机系统

测速发电机是将角速度信号转换成电压信号的测速装置，在机电伺服系统中常用作局部反馈元件。测速发电机有交流、直流之分，如图2-7所示。

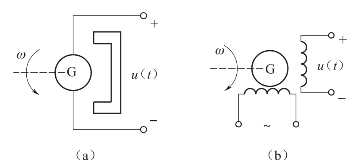
图2-7　测速发电机系统示意图

(a)直流测速发电机；(b)交流测速发电机

永磁式直流测速发电机的转子与待测轴相连，输出与转子转轴角速度成正比的电压信号。交流测速发电机有两个互相垂直放置的线圈，一个是激磁绕组，接入一定频率的正弦额定电压信号，另一个为输出绕组，当转子旋转时，输出绕组产生与转轴转速成比例的交流电压信号，其频率与激磁电压频率相同，若输出电压的包络用u(t)表示，则两种发电机输出、输入关系都可以表示为

式中，K表示测速发电机的转换系数(V·s/rad)。

一般情况下，应将微分方程写为标准形式，即与输入量有关的项写在方程的右端，与输出量有关的项写在方程的左端，方程两端变量的导数项均按降幂排列。