变压器的损耗主要包括铁损P_Fe和铜损P_Cu两部分，对驱动电路的稳定工作和整机效率有重要影响。

1.铁损

铁损即磁心损耗，主要包括磁滞损耗P_h、涡流损耗P_e和剩余损耗P_r。

（1）磁滞损耗P_h

由于变压器铁心存在磁矫顽力，当励磁电流产生的磁场对变压器铁心进行磁化结束以后，磁通密度不能跟随着磁场强度下降到零，也就是说励磁电流或磁场强度从最大值下降到零，但是磁通密度却没有跟随磁场强度下降到零，而是停留在了剩余磁通密度B_r位置上。所以在交流磁场反复对变压器铁心进行磁化的过程中，总是需要一部分的磁场能量来克服磁矫顽力和消除剩余磁通，这部分能量对于变压器铁心来说并没有起到增强磁通密度的作用，是一种损耗；另外因为磁感应强度的变化总是落后于磁场强度，所以把这种损耗称为磁滞损耗。

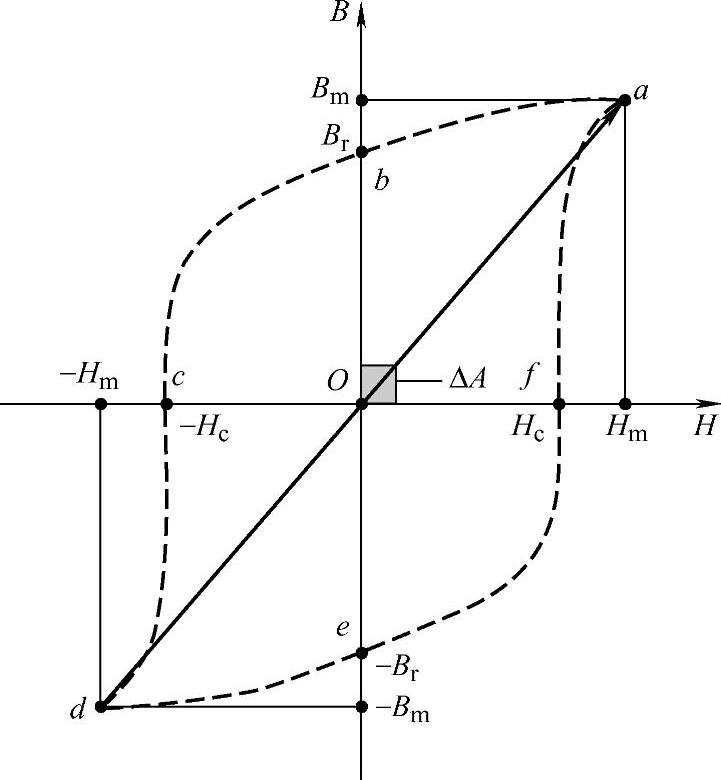
图10-3 磁化曲线

变压器铁心的磁化曲线如图10-3所示，图中直线d-O-a是变压器铁心的理想磁化曲线，虚线a-b-c-d-e-f- a是实际的磁滞回路曲线，它与理想的磁化曲线d-O-a（实线）相比，多走的弯路要损耗电磁能量，这种损耗就是磁滞损耗。在封闭曲线a-b-c-d-e-f a任意取一小块面积ΔA，其值可以任意小，以保证在此面积中变压器铁心的磁导率可以看成常数。与ΔA面积对应的磁通密度增量为ΔB，磁场强度增量为ΔH，时间增量为Δt。因此有

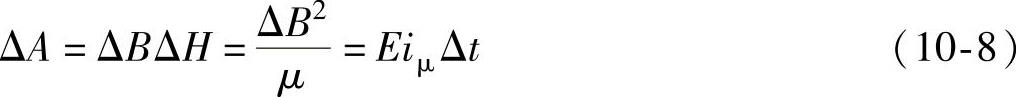
式中，μ为磁导率；Δt为时间增量；E为单位长度导线产生的感应电动势；i_μ为励磁电流。

在实际电路中，磁场强度是由励磁电流通过变压器一次线圈产生的，所谓的励磁电流，就是让变压器铁心进行充磁和消磁的电流。由公式（10-8）可以看出，虚线a-b-c-d-e-f-a所围区域的面积对应的就是磁滞损耗的能量，所以磁滞损耗能量的大小与磁滞回线的面积成正比。

输入交流脉冲在一个周期内，变压器铁心中的磁通密度正好沿着磁滞回线走一圈，因此对公式（10-8）进行积分，即可求得变压器铁心在一个周期内的磁滞损耗，即

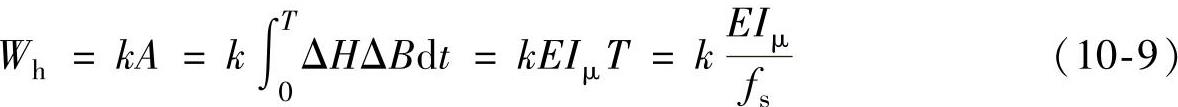
式中，W_h为一个周期内变压器铁心的磁滞损耗；I_μ为励磁电流的平均值；T为输入交流电压的周期；f_s为电源的工作频率；k为比例系数，它是一个与选用单位制和变压器铁心面积、体积以及一次线圈匝数等参数相关的常量。

把公式（10-9）两端乘以频率，即可得到磁滞损耗的功率表达式，即

P_h=f_sW_h=kEI_μ （10-10）

磁滞损耗可进一步用Steinmetz方程式表示为

P_h=k_hf_sB_mV （10-11）

式中，k_h为磁滞损耗系数；V为磁心体积。

由式（10-11）可以看出，频率越高磁滞损耗越大；磁感应摆幅越大，磁滞回线包围面积越大，损耗越大。

（2）涡流损耗P_e

涡流损耗P_e的产生，是在磁心线圈中加上交流电压时，线圈中流过励磁电流，磁势产生的全部磁通Φ在磁心中通过，如果磁心是一个导体，磁心本身截面周围也将链合全部磁通Φ而构成单匝的二次线圈。当交流励磁电压为u₁时，根据电磁感应定律有

式中，N₁为磁心线圈的匝数。

每一匝的感应电动势，即磁心截面最大周边等效一匝感应电动势为

因为磁心材料的电阻率不会无限大，绕着磁心周边有一定的电阻值，感应电压产生涡流i_e流过这个电阻R，引起i²_eR的涡流损耗。由上面分析可以看出，涡流损耗与磁心磁通变化率成正比，涡流i_e则与每匝伏特和占空比有关，而与工作频率无直接关系，但频率提高可以使磁通变化率提高从而影响涡流损耗，或者因频率提高而减少匝数从而影响涡流损耗^[1]。涡流一方面产生磁心损耗，另一方面产生的涡流所建立磁通阻止磁心中主磁通变化，使得磁通趋向磁心表面，导致磁心有效截面积减少，这种现象就是趋肤效应。

实际应用中涡流损耗可用Steinmetz方程式表示为

P_e=k_e（f_sB_m）2V （10-14）

式中，k_e为涡流损耗系数。

（3）剩余损耗P_r

剩余损耗P_r是由于磁化弛豫效应或磁性滞后效应引起的损耗。所谓弛豫，是指在磁化或反磁化的过程中，磁化状态并不是随磁化强度的变化而立即变化到它的最终状态，而是需要一个过程，这个时间效应就是引起剩余损耗的原因^[2]。(www.daowen.com)

实际应用中剩余损耗可用Steinmetz方程式表示为

P_r=k_r（f_sB_m）^1.5V （10-15）

式中，k_r为剩余损耗系数。

综上分析可见，在交变磁场中，磁心单位体积能量损耗既取决于磁介质本身的电阻率、结构形状等因素，又取决于交变磁场的频率和磁感应强度摆幅ΔB_m。在低频时，铁损（即磁心损耗）几乎完全是磁滞损耗；开关电源其工作频率一般在10kHz以上，此时涡流损耗和剩余损耗已超过磁滞损耗。总的磁心损耗可以表示为^[1]

P_Fe=ηf_s^αB^β_mV （10-16）

式中，η为损耗系数；f_s为电源工作频率；B_m为磁心磁感应强度幅值；α和β分别为大于1的频率损耗指数和磁感应损耗指数。

2.铜损

变压器铜损的一般计算公式为

P_Cu=I²_rmsR_dc （10-17）

式中，R_dc为绕组导线的直流电阻；I_rms为绕组电流的有效值。

由于交流输入时的趋肤效应和邻近效应，绕组铜损往往比上述公式的计算值大很多，此时变压器绕组的铜损应包括直流损耗与交流损耗。

（1）直流损耗

直流损耗主要指因为绕制变压器的导线具有直流阻抗，当通过工作电流直流分量I_dc时引起的功率损耗。对于高频变压器来说，其绕组的直流阻抗R_dc的计算公式为

式中，l为线圈总长度；A_Cu为铜导线截面积；ρ（T）为温度为T（℃）时的导线电阻率（Ω·m²/m），关系式为

ρ（T）=1.59×10^-8+6.77×10^-11T （10-19）

（2）交流损耗

交流损耗指工作电流的交流分量在绕组交流电阻R_ac上引起的功率损耗，交流损耗影响因素较多，包括绕组的趋肤效应和邻近效应引起的损耗，以及谐波引起的损耗，一般邻近效应比趋肤效应引起更严重的交流损耗。这些影响因素导致等效交流电阻R_ac的理论计算非常复杂，因此应用时一般采用Dowell方法。

当流过高频电流时，由于趋肤效应导致电流从导体表层流过，此表层的厚度为穿透深度或趋肤深度Δ。穿透深度与工作温度、导体电阻率、导体磁导率以及频率等因素有关，工作频率越高，导线的穿透深度就越低，可表示为

式中，γ为导线的电导率；μ为导线的磁导率。

进一步定义Q为等效铜层厚度，表示为

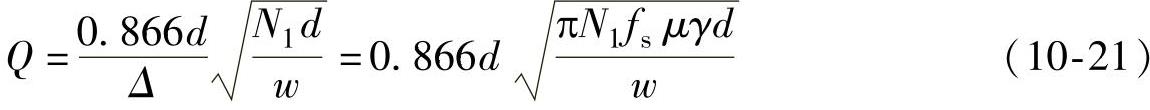
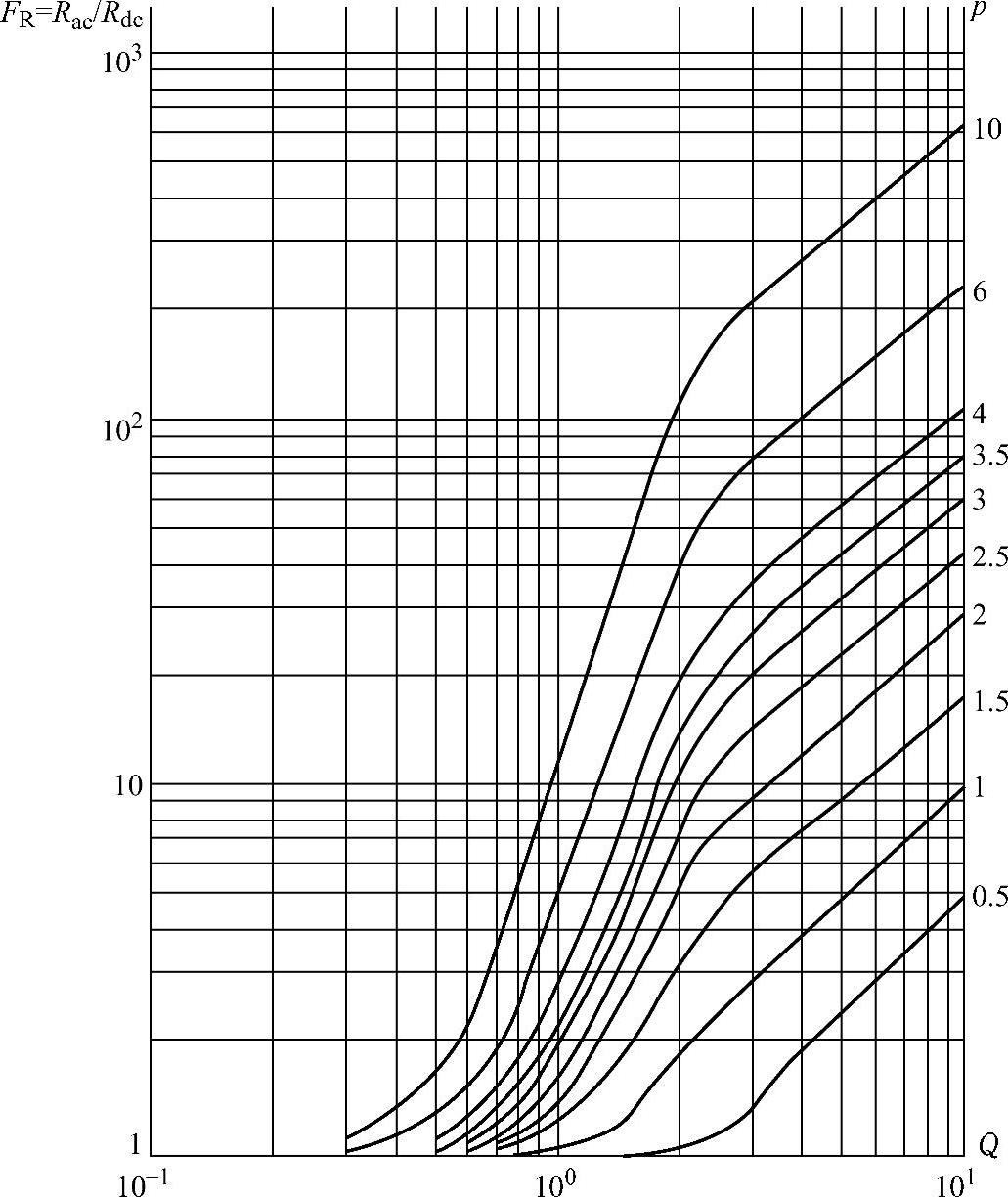
图10-4 Dowell曲线

式中，d为导线直径；N₁为每层匝数；w为绕组层宽度。

Dowell提出了基于正弦激励的变压器一维模型铜损计算方法，并根据分析得到如图10-4所示的Dowell曲线，它描述了交直流阻抗比F_R（F_R=R_ac/R_dc）与等效铜层厚度Q、层数p的关系^[3]。图10-4中，根据式（10-21）求得Q后，结合线圈绕组层数p，即可求得纵坐标F_R=R_ac/R_dc，进一步根据直流电阻R_dc可求得交流电阻R_ac。则变压器的铜损P_Cu为

P_Cu=I²_dcR_dc+I²_acR_ac （10-22）

将公式（10-16）和公式（ 10-22）相加得到变压器总损耗为

P_tran=P_Fe+P_Cu （10-23）

通过以上分析，可以看出在一定的绝缘等级和应用环境条件下，选取较高的B_m会使磁心损耗增加，但线圈匝数会减少，导线电阻减少，变压器铜损会下降；反之，铜损增加，而磁心损耗减少。