1.等效电路
对于谐振变换器的特性分析通常采用一次基波近似法(First Harmonic Approximation,FHA),该方法假设输入到输出能量的转移主要是由电压以及电流的傅里叶级数的基波分量组成的,下面通过FHA采用交流电路分析法对半桥LLC谐振变换器进行分析[10]。
图3-28所示为半桥LLC的输入FHA电路,半桥两开关管Q1和Q2交替导通,其占空比为0.5。因此,谐振电路的输入电压US是一方波,其幅值为UIN,平均值为UIN/2,UIN的一次基波电压US1为


图3-28 输入FHA电路
在实际的电路中,二次侧整流二极管上流过的电流为准正弦波,电流到零时翻转,故整流电路的输入电压为一方波,其幅值为UO,电压、电流同相位。输出FHA等效电路如图3-29所示。
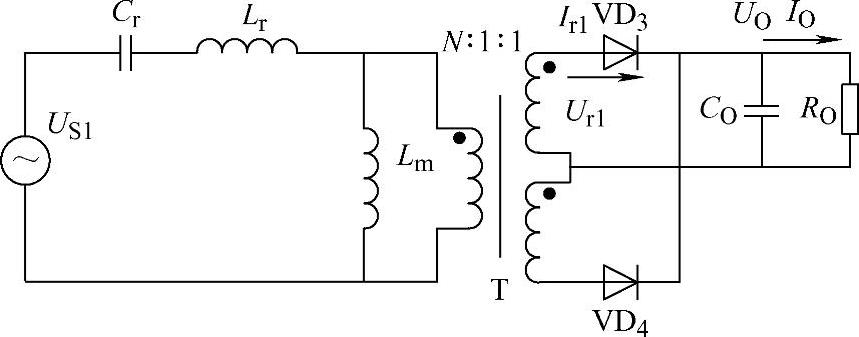
图3-29 输出FHA电路
由此,可得出该方波电压的傅里叶级数表达式,即
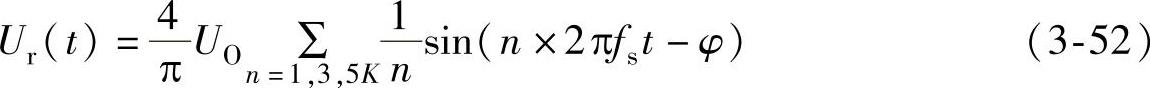
式中,φ为Ur(t)与输入电压一次基波分量US1的相位差。
将输出侧电压、电阻等效到一次侧可得等效电路,如图3-30所示。由于变压器匝数比为N∶1∶1,所以可得等效后的电阻、电压表达式为


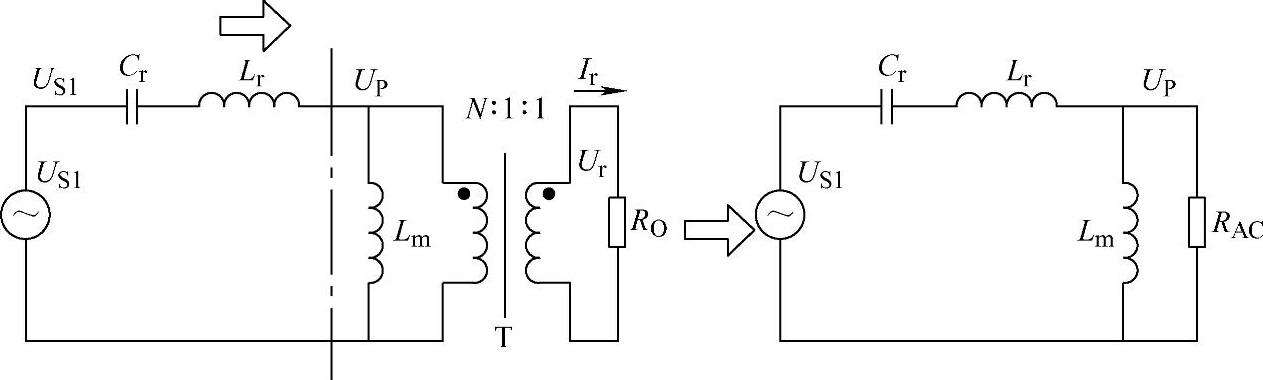
图3-30 FHA等效电路
通过上面的分析,可以得到LLC的简化FHA等效电路,如图3-31所示。

图3-31 简化FHA等效电路
2.参数设计计算
LLC谐振电路的电压增益表示为

因此,归一化电压增益可等效为谐振电路输出阻抗与输入阻抗的比值,其表示为
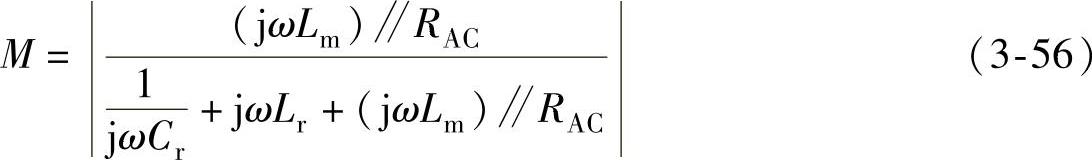
定义谐振网络阻抗为

谐振网络的品质因数为

电感系数为

归一化频率为

将式(3-58)~式(3-60)代入式(3-56)中得
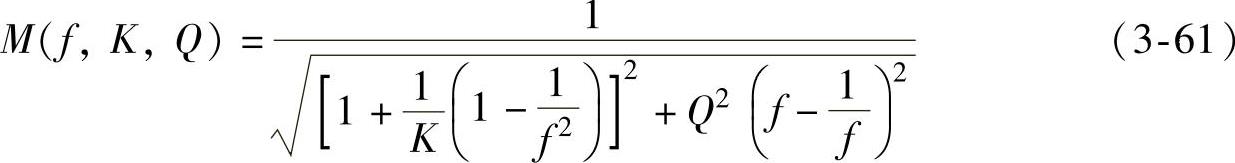
电压增益是关于电感比K、电路品质因数Q、归一化频率f的函数,为了更直观地分析f、K、Q对电压增益的影响,可以先固定其中一个变量,使用MathCAD绘制出LLC谐振变换器电压增益的曲线,对另外的变量进行讨论。
(1)电路品质因数Q的影响
给定K=4,绘出Q=0.2、0.4、0.6、0.8、1时电压增益与归一化频率f的一系列函数曲线,如图3-32所示。
 (https://www.daowen.com)
(https://www.daowen.com)
图3-32 LLC谐振变换器典型增益曲线(K=4)
从图3-32中可以看出,所有的曲线都相交于一点,此点的开关频率f等于谐振频率fr,谐振电路的电压增益为1,电路特性与负荷基本没有关系,该点称为一个独立工作点,这是LLC谐振变换器性能好于串联谐振变换器、并联谐振变换器等常规谐振变换器的明显特征。因此,在进行参数设计时,最好使LLC谐振变换器工作在该谐振频率的附近。随着Q值的增加,电压增益的峰值呈减小趋势,为了保证在最小输入电压下仍能够达到需要的输出电压值,在谐振网络的设计中,Q值就不能选择过大。同时,随着Q值的减小,会相应地使谐振电感的值减小,增大一次循环电流,增加损耗,降低整体电路的效率[11]。因而,Q的取值必须兼顾多方面因素,综合考虑。
(2)电感比K的讨论
给定Q=0.4,绘出K=1、3、5、7、9时电压增益与归一化频率f的函数曲线,如图3-33所示。

图3-33 LLC谐振变换器典型增益曲线(Q=0.4)
从图3-33中可以看出,随着K值的增加,电压增益的峰值降低,这意味着谐振变换器可以调节的电压范围减小,当输入电压处于最小值时,谐振变换器的输出电压可能无法调节到需要的恒定电压值;同时,从图中还可以看到K值越大,要获得同样的增益,频率变化的范围就相对比较宽一些,这样不利于磁性元器件的正常工作[12]。因此,在进行参数设计时,K值不能过大。而如果减小K值,这意味着减小了并联谐振电感,则电感上的电流就增大,电感上的损耗增大。因此需要在增益范围和功率损耗之间折中选取K值,一般取2.5~6。
变压器的理论匝数比为N,考虑二次侧整流二极管的导通压降UDF,则

在Q=0时(空载状态下),电压增益为

空载状态下的电压增益随着归一化频率趋于无穷大时趋于最小值,其值为
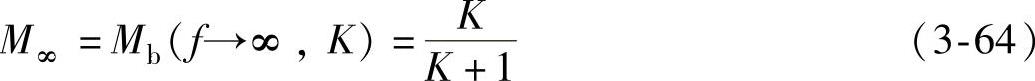
输入电压最大时,得到半桥LLC谐振电路的最小电压增益MMIN,为了保证此时仍能工作在空载状态,应使MMIN>M∞,即
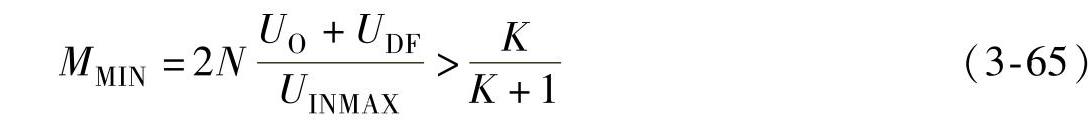
由式(3-65)可以设计电感系数K,进一步可设计谐振电感参数。
电压增益的最大值MMAX决定了变换器工作时的最低频率,半桥LLC谐振电路的最大电压增益为

允许半桥LLC谐振电路最大增益在分界线上工作的最小归一化频率为[13]
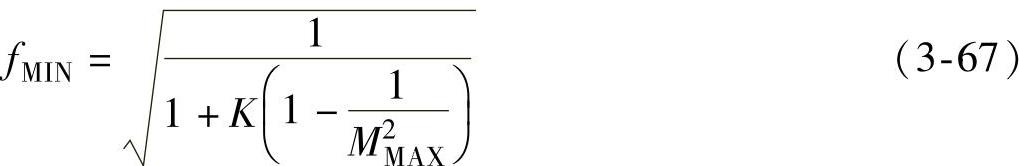
电压增益的最小值MMIN决定了变换器工作时的最高频率,半桥LLC谐振电路允许工作的最大归一化频率为

结合式(3-60)即可设计变换器工作的最低频率和最高频率。
变换器在最低工作频率fMIN时得到的最大品质因数为
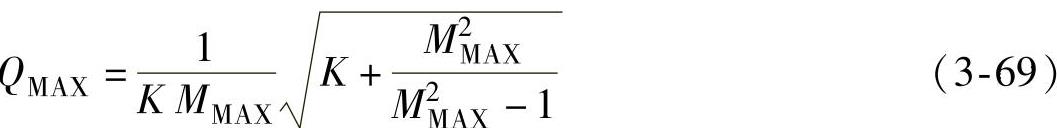
在进行FHA分析时,为求简化可将开关网络中各点处的寄生电容忽略不计。但当开关管工作在ZVS状态时,这些寄生电容对电路的工作和性能起到重要作用,因此应加以考虑[13]。如果Q1和Q2漏、源极间的寄生电容C1和C2的容值为Coss,对地的寄生电容C3与谐振电路相互并联,其容值为Cstray,具体分布电路如图3-34所示。
所以,工作于ZVS状态时,中点N处的总电容为
CZVS=2Coss+Cstray (3-70)
在ZVS状态下,输入电压最小、满载情况下的最大品质因数QZVS,1为
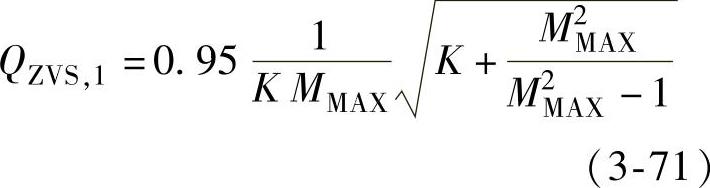
在ZVS状态下,死区时间为Tdead,输入电压为最大、负载为空载情况下的最大品质因数QZVS,2为
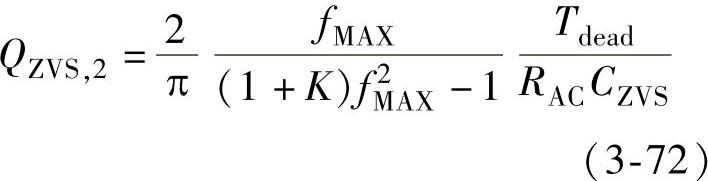
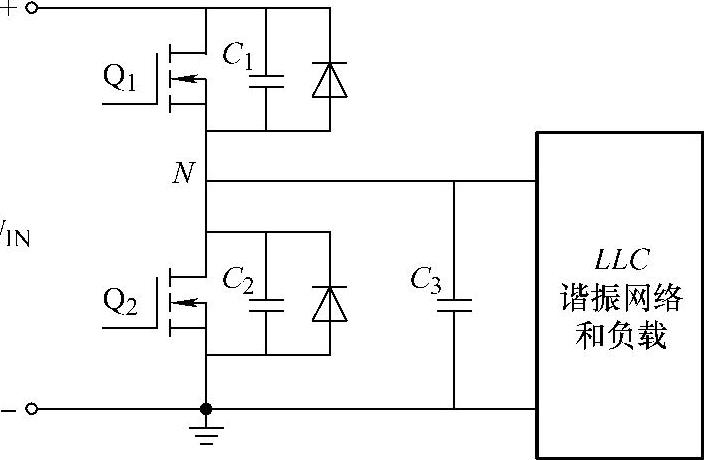
图3-34 寄生电容分布
为使变换器在工作范围内实现ZVS,应综合考虑式(3-71)、式(3-72)中的条件,选取品质因数的最大值为
QZVS≤min{QZVS,1,QZVS,2} (3-73)
根据品质因数Q及其他参数,可以设计谐振电容和电感值为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







