上面的讨论表明,对大柔度压杆,可用欧拉公式计算临界压力Fcr。对欧拉公式不适用的压杆,可由经验公式计算临界应力σcr,再乘以截面面积求得临界压力Fcr。以稳定安全因数nst除Fcr可得到许用压力[F]。压杆的实际工作压力F不应超过[F],故压杆的稳定条件为

以上稳定条件也可写成比较安全因数的形式,即要求压杆的工作安全因数n(临界压力Fcr与工作压力F之比)不小于规定的稳定安全因数nst,即

规定的稳定安全因数nst一般要高于强度安全因数。这是因为实际中存在一些难以避免的因素,如杆件的初弯曲、压力偏心,材料不均匀和支座的缺陷等,这些因素都严重影响压杆的稳定性,降低临界压力。

当压杆在局部有截面削弱时,如在压杆中有螺钉孔等情况,由于压杆的临界压力是由压杆的整体变形来决定的,局部的截面削弱对压杆的整体变形影响很小,因此在计算临界压力的公式中,I和A都按没削弱的横截面尺寸来计算。对于局部有截面削弱的压杆,除了要进行稳定校核外,还应该对压杆削弱了的截面进行强度校核。在强度条件中的工作应力,应按削弱了的截面面积(净面积)进行计算。

例13-3　空气压缩机的活塞杆由45钢制成,σs=350MPa,σp=280MPa,E=210GPa。活塞杆长度l=703mm,直径d=45mm,最大压力Fmax=41.6kN,规定安全因数nst=8。试校核活塞杆的稳定性。

解:由式(13-16)可求得

活塞杆两端可以视为铰支座,因此μ=1。柔度

可见λ＜λ1,故不能使用欧拉公式计算临界压力。如采用直线公式,由表13-2查得优质碳钢的a=461MPa,b=2.568MPa,由式(13-19)得

可见活塞杆的λ介于λ2和λ1之间,为中等柔度压杆,由直线公式求得

活塞的工作安全因数

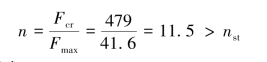(www.daowen.com)

故此活塞杆满足稳定性要求。

例13-4　某液压传动装置的油缸活塞直径D=65mm,油压p=1.2MPa,活塞杆长度l=1250mm,材料为35钢,σp=220MPa,E=210GPa,nst=6。试确定活塞杆的直径。

解:活塞杆承受的轴向压力

在稳定条件式取等号,活塞杆的临界压力

现需确定活塞杆的直径d,使活塞杆具有23892N的临界压力。然而,在直径确定之前,无法求出活塞杆的柔度λ,也不能判定用欧拉公式还是用经验公式。因此,先用欧拉公式进行试算,得出活塞杆直径后,再检验是否满足使用欧拉公式的条件。

活塞杆两端约束可视为铰支,由欧拉公式得

由此可解出d=0.0246m,取d=25mm。

计算活塞杆的柔度

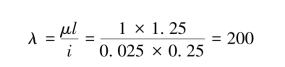
由式(13-16)可求得

可见λ＞λ1,故用欧拉公式进行的试算是正确的,活塞杆直径可取25mm。

思政提示

试算法是工程设计中常用的一种方法。在解决实际问题,保证安全和影响可控前提下,不妨大胆创新,试用不同的方法,然后在实践中检验是否有效。