当杆端为其他约束情况时,细长压杆的临界压力公式可以仿照上节中的方法,根据在不同的杆端约束情况下压杆的挠曲轴近似微分方程式和挠曲轴的边界条件来推导。也可以利用两端铰支细长压杆的临界压力公式,得到其他杆端约束情况下细长压杆的临界压力公式。从上节中推导临界压力公式的过程可知,两端铰支细长压杆的临界压力和该压杆的挠曲轴形状有联系。由此可以推知,两压杆的挠曲轴形状若相同,则两者的临界压力也应相同。根据这个关系,可利用式(13-8)来得到其他杆端约束情形下细长压杆的临界压力公式。

首先来研究长为l的两端固定的细长压杆。在此压杆的挠曲轴中,距上、下两端各l/4处有两个拐点A、B,如图13-4(a)所示。在A、B两点间的一段曲线形状和两端铰支长为l/2的压杆的挠曲轴形状相同,如图13-4(b)所示,都是半波的正弦曲线。于是,杆AB段的临界压力就可以按两端铰支细长杆的临界压力公式(13-8)来计算,但应将公式中的杆长用AB段的长度l/2代入,即

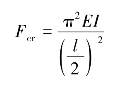
由于杆AB段是两端固定压杆中的一部分,所以其临界压力就是所研究的两端固定压杆的临界压力,因而上式也就是长度为l的两端固定细长压杆的临界压力公式。

再研究长为l的一端固定另一端自由的细长压杆,其挠曲轴形状和长为2l的两端铰支压杆挠曲轴的上半段形状相同,是1/4波的正弦曲线,如图13-5所示。所以,依照前面推理,可知长为l的一端固定另一端自由细长压杆的临界压力和长为2l的两端铰支细长压杆的临界压力相同,后者可将杆长2l代入式(13-8),求得临界压力为

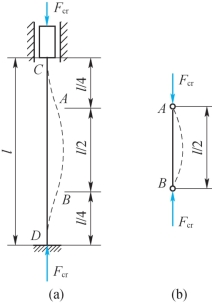
图13-4

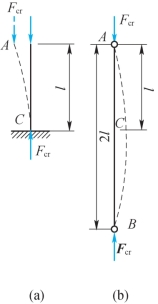
图13-5

至于长为l的一端固定另一端铰支的细长压杆的临界压力公式可按照上一节中介绍的方法,根据其挠曲轴近似微分方程式以及相应边界条件求得,即

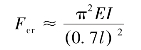
上述结果可归纳为细长压杆临界压力公式的统一形式

式中,μl称为压杆的相当长度,而μ称为长度因数。

几种理想的杆端约束情况下压杆的长度因数如表13-1所示,表中挠曲轴上的C、D点为拐点。

表13-1

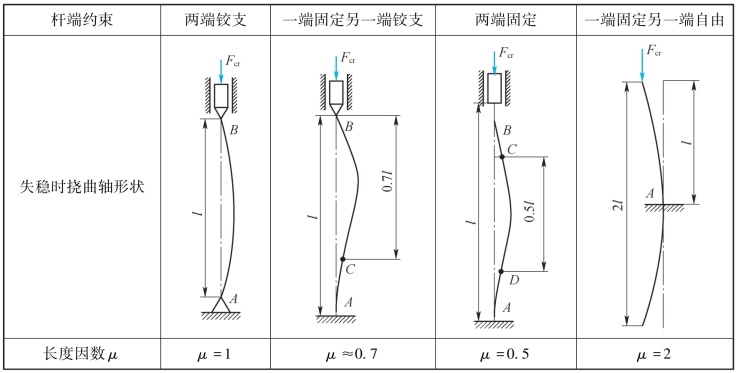
以上所讨论的压杆的长度因数μ都是对理想的杆端约束情况而言的。从表13-1中可以看出,两端都有约束的压杆,其长度因数在0.5～1.0的范围以内。在实际情况下,端部固定的压杆其杆端很难做到完全固定;只要杆端面稍有发生转动的可能,这种杆端就不能看成理想的固定端,而是一种接近于铰支端的情况。所以在上述情况下,常将压杆的长度因数μ取为接近于1.0的值。在各种实际的杆端约束情况下,压杆的长度因数在一般的设计规范中都有具体的规定。

例13-2　如图13-6所示,下端固定、上端自由的等截面细长中心受压直杆,长度为l,抗弯刚度为EI。试推导其临界力Fcr的欧拉公式,并求出压杆的挠曲轴方程。

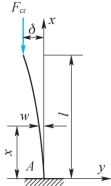
图13-6

解:由杆端约束条件,最大挠度δ出现在杆的自由端。由临界压力所引起的杆的任意位置x处的横截面上的弯矩可表示为

式中,w为x处杆的挠度。则挠曲轴的近似微分方程为(www.daowen.com)

记k2=Fcr/EI,上式简化为

该微分方程的解为

w的一阶导数为

待定常数A、B、k由挠曲轴的边界条件来确定,边界条件为

将式(c)代入式(a)、式(b),得A=0,B=-δ。式(a)可变为

将式(d)代入式(e)得

所以

从而得到

取最小解kl=π/2,得该压杆临界压力

将k=π/2l代入式(e),则可得挠曲轴方程为

式中,δ为杆自由端的微小挠度,在挠曲轴的近似微分方程推导过程中,其值不确定。

思政提示

通过引入不同长度因数,把不同约束条件下压杆临界压力的公式统一起来。客观事物都是复杂多样的,我们在学习过程中要注意对同类事物的归纳总结,这样便于我们更深入地理解和掌握知识。