设细长中心受压直杆的两端为球铰支座,当压力达到临界值时,压杆将由直线平衡形态转变为曲线平衡形态。可以认为,使压杆保持微小弯曲平衡的最小压力即为临界压力Fcr。

选取坐标系如图13-2所示,距原点距离为x的任意截面的挠度为w=w(x),弯矩M的绝对值为Fw。取压力F的绝对值,则w为正时,M为负;w为负时,M为正。即M与w的符号相反,所以

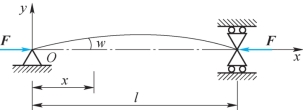
图13-2

对微小的弯曲变形,挠曲轴的近似微分方程为

由于两端是球铰,允许杆件在任意纵向平面内发生弯曲变形,因而杆件的微小弯曲变形一定发生于抗弯能力最小的纵向平面内。所以,上式中的I应是横截面最小的惯性矩。将式(13-1)代入式(13-2),得

引用记号

于是式(13-3)可以写成

以上微分方程的通解为

式中,A、B为积分常数。杆件的边界条件为x=0和x=l时,w=0。由此求得B=0,Asinkl=0。由此可得,A或者sinkl等于0。但因B已经为0,如A再等于0,则由式(13-6)知w≡0,这表示杆件轴线上任意点的挠度为0,杆件轴线仍为直线。这与杆件失稳发生微小弯曲的前提矛盾。因此,只能是sinkl=0。于是kl为数列0,π,2π,3π,…中任意一个数,或者写成kl=nπ(n=0,1,2,…)。将k代入式(13-4),得出

(www.daowen.com)

因为n=0,1,2,…,故上式表明使杆件保持为曲线平衡的压力,理论上是多值的。在这些压力中,使杆件以微小弯曲形态平衡的最小压力,才是临界压力Fcr。然而取n=0,则F=0,表示杆件上并无压力,这自然不是我们所需的,因此只有取n=1。于是得临界压力

这就是两端铰支细长压杆临界压力的计算公式,也称为两端铰支压杆的欧拉公式。

导出欧拉公式时,用变形后的位置计算弯矩,如式(13-1)所示。这里不再使用“原始尺寸原理”,这是稳定性问题在处理方法上与以往不同之处。

下面讨论压杆的挠曲轴近似微分方程。取n=1时,k=π/l。再注意到B=0,于是式(13-6)化为

x取值范围为(0,l),可见压杆过渡为曲线平衡后,挠曲轴为半波正弦曲线。A是杆件中点(即x=l/2处)的挠度,它的数值无法确定,这是因为在推导过程中使用了挠曲轴的近似微分方程。若以横坐标表示挠曲轴中点的挠度wm,纵坐标表示压力F,如图13-3所示。当F小于Fcr时,杆件的直线平衡是稳定的,wm恒为0,F与wm的关系如与纵坐标轴重合的直线Oa所示。当F到达Fcr时,直线平衡变为不稳定,过渡为曲线平衡,wm不等于0但数值未定,F与wm的关系如水平线ab所示。若采用挠曲轴的精确微分方程,则挠曲轴中点挠度wm与压力F之间的关系如曲线ac所示。

图13-3

以上讨论中,假设压杆是理想的中心受压直杆。实际压杆难免有初弯曲、压力偏心、材质不均匀等情况,这些缺陷相当于压力有一个偏心距,因而在压力远小于Fcr时,杆件已开始有弯曲变形。试验结果如图13-3中曲线Od所示。可以把折线Oab看作曲线Od的极限情况。

例13-1　柴油机的钢制空心圆管挺杆,内径和外径分别为10mm和12mm,杆长383mm,材料弹性模量E=210GPa。挺杆两端视为铰支座约束,试计算该挺杆的临界载荷。

解:挺杆横截面惯性矩为

由式(13-8)得挺杆临界压力为

思政提示

条件不同或所研究问题不同,情况就会随之改变。同样是受压杆,轴向拉伸和压缩是强度问题,随着条件改变,就成了压杆稳定性问题。一直利用的原始尺寸原理,本节因为研究的稳定性问题与变形后产生弯矩有关,所以原始尺寸原理不再适用。